引入势场及陷阱搜索的强化学习路径规划算法

董培方，张志安，梅新虎，朱 朔

DONG Peifang1,ZHANG Zhi’an1,MEI Xinhu2,ZHU Shuo1

1.南京理工大学 机械工程学院，南京 210094

2.南京理工大学 计算机科学与技术学院，南京 210094

1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

2.School of Computer Science and Technology,Nanjing University of Science and Technology,Nanjing 210094,China

1 引言

随着无人驾驶的兴起，移动机器人路径规划技术越来越受到人们的重视。作为移动机器人自主移动的核心技术，有大量的科研人员投入到相关的研究工作中。传统的路径规划技术有人工势场法、图解法、动态窗口法[1]等，基于人工智能的路径规划技术有遗传算法[2]、神经网络[3]、蚁群算法[4]等，每种方法都存在一定的局限性。传统方法在复杂的环境地图中易陷入陷阱中无法逃逸，有较大的概率无法到达目标位置；而智能算法计算量庞大，需要进行较多的迭代次数之后才能规划成功。强化学习算法是根据奖励和惩罚机制来提高对特定任务的完成能力，其探索和贪心思想适用于未知环境中的路径规划，随机探索的概率越大则最终获得的路径越优，理论上能满足任意复杂环境的路径规划，具有较强的可开发性。

Q学习（Q-learning）算法是强化学习中的一种高效离策学习算法，传统的Q-learning算法基于马尔可夫过程，采用随机初始化，对环境的先验信息为0，初始路径较为随机，导致路径规划效率低下，训练所需的迭代次数过多。基于此，研究人员提出了多种方法初始化Q值函数加快路径规划的迭代速度，有神经网络法、模糊规则法[5]、人工势场法[6-8]等。人工势场法规则简单，效率较高，但在复杂环境中基于障碍物的斥力势场数量多，计算量大。针对Q-learning算法的迭代速度慢，本文提出了引力势场和环境陷阱搜索联合作为先验信息初始化Q值，避免了复杂环境中斥力势场庞大的计算量，同时有效防止了移动体陷入环境中的凹形陷阱，加快了算法的迭代速度。同时取消对障碍物的试错学习，缩小可行路径的范围，使训练能应用于真实环境中。最后，通过python及pygame模块在复杂环境中进行仿真实验，验证了算法的可行性和高效性。

2 强化学习机制

强化学习方法是指智能体（agent）通过在环境中按照一定的策略探索，根据环境的奖励和惩罚机制不断调整行为策略，以获得最大的回报值作为最终行为目的。在标准的强化学习框架中，包括智能体（agent）、环境及4个基本要素[9]。

（1）策略（policy）

策略π是智能体与环境交互时的行为选择依据，S→A是状态空间到动作空间的映射，智能体在状态St下根据π选择动作at+1∈A。

（2）奖惩函数（reward）

奖惩函数r反映当前环境状态St∈S（S为状态空间集）下的动作at∈A（A为动作空间集）对达成目标的贡献度，r值越大代表当前环境下的动作越有利于达成目标。

（3）值函数（value function）

值函数V是agent在环境下行动的期望回报，强化学习通过不断地试错来迭代值函数，以获得较大期望回报，用于提高高回报值的状态动作选择概率而降低低回报值的环境状态选择概率。

通过对值函数评估来不断改变对应状态的行动策略，以达到最大化回报：

（4）环境模型（model of environment）

环境模型强化学习的基本运行环境，包括环境状态及其对应的动作映射空间。

3 Q-learning算法模型

Q-learning算法是基于时序差分（Temporal-Difference，TD）误差的离策强化学习算法，采用了动态规划的思想，根据下一步的最大动作-状态值函数作为动作选择的策略：

基于Q-learning的强化学习方法建立在马尔可夫决策过程理论框架上，即智能体与环境的交互过程中，t时刻的状态St只与上一个状态S(t-1)下所采取的动作a(t-1)有关，而与历史状态和动作无关，即：

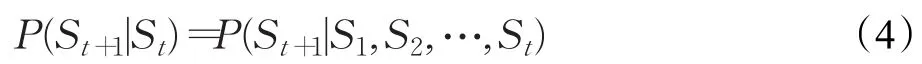
Q-learning更新函数：

其中，α为学习率，学习率越大，迭代速度越快，但易过拟合；γ为折扣率，即未来奖励对当前动作的影响程度[10]。

4 加入环境初始信息的快速Q-learning迭代算法

传统的Q-learning算法无环境先验信息，初始状态的所有状态值函数V(s)均相等或完全随机，每一步动作a产生于随机状态，即此时的MDP环境状态转移概率是均等的。对于路径规划问题而言，只有在达到目的地或者碰到障碍物才会更改回报值R，进行一次有效的状态-动作值更新，回报函数的稀疏性致使初期的规划效率低，迭代次数多，特别对于尺度较大的未知环境，易出现巨大的无效迭代搜索空间[11-12]。

结合人工势场法和陷阱搜索的基本思想改进基于Q-learning算法的路径规划：

（1）确定起始点坐标a和目标点坐标b，在初始化状态值函数中以目标点为势场中心建立引力势场，根据目标点的位置作为环境先验信息初始化V(S)表，设定初始化后的V(S)值均大于等于0。

（2）对环境地图进行4个方位的逐层搜索，若发现障碍物，则进行V(S(t+1))=-A操作，若发现陷阱区域，则对该区域进行逐层向外搜索，每层之间设置梯度值-B,并通过Lmax＜A/B，保证陷阱区的最外层状态值为负数。

（3）利用环境状态值函数更新状态-动作值函数表：

（4）智能体从起始点开始探索环境，只把V(S(t+1))≥0的状态作为可探索状态，采取可变贪心法则，每移动一步更新一次状态-动作值。到达目标点后结束此轮迭代，从起始点开始进入下一轮探索。

4.1 改进人工势场法

人工势场法的基本原理是在目标物周围产生虚拟引力势场，智能体在任何位置都受到来自目标点的引力吸引，而障碍物对移动物体产生排斥力，阻止物体靠近产生碰撞[13]。

引力势场函数：

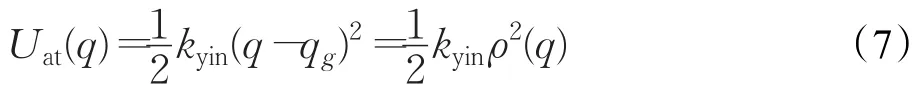
式中，kyin为引力常数；ρ(q)=||q-qg||是智能体与目标位置的欧几里德距离。

基于改进引力势场法初始化状态值函数法则：Q-learning算法是基于马尔科夫决策的无模型强化学习算法，采用可变ξ-greedy法则[14]，其行为策略是往Q值增大的方向移动，因此对于初始化状态值函数表，应满足距离目标点越近其引力势场越大，与距离成反比（传统的引力势场与距离平方成正比），为了保证算法的实时性，不考虑障碍物的斥力势场，同时减小公式计算复杂度，引入参量L用于调整初始状态值的变化范围：

D(Pinit,Pgoal)=为起始点和目标点之间的距离。

对于复杂环境的Q-learning算法路径规划，动作状态空间庞大，迭代速度慢，引入目标点改进引力势场来初始化状态值函数，从而提供初始目标位置，智能体具有目标趋向性，能迅速朝目标方向移动，同时随机策略保证其不陷入局部最优解。

4.2 环境陷阱搜索算法

在复杂环境中，常常存在凹形障碍物，对于人工势场法或蚁群算法等易陷入凹形区域，无法到达目标点。基于强化学习算法的路径规划能够通过随机探索策略和策略改进逃离此类障碍物，这种智能行为是高效导航基础[15]，但规划效率低，只引入引力势场的强化学习算法由于目标趋向性同样容易陷入与目标相对的凹形障碍物中，需要较多的训练次数才能逃逸，如果能直接将凹形障碍物从可行的规划路径中剔除，则能提高规划的效率，减少迭代的次数。

针对此类障碍物，提出沿x、y方向的陷阱逐层搜索，并把搜索结果作为环境先验信息初始化状态函数表V(S)。

陷阱搜索算法如下：

步骤1将探索环境栅格化，并对障碍物进行膨胀处理，将移动物体（agent）看作质点。以地图某一顶点作为坐标原点建立直角坐标系（如图1所示，黑色为障碍区，白色为可行区域）。建立当前层疑似陷阱长度存储数组Suspect-trap[]、层数存储数组Trap-length[]以及当前层陷阱个数存储数组Trap-number[]。初始点坐标为a(x,y)，目标位置的坐标为b(x,y)。对栅格地图进行4个方向的逐层搜索，如图1为沿X正方向进行层内搜索，Y正方向进行层级搜索，即沿栅格内数字顺序搜索。

图1 栅格地图

步骤2利用改进人工势场法初始化状态函数表，距离目标点越近，状态值越大，非障碍物区域状态值大于等于0，障碍物区域状态值为-A(A＞0)，陷阱层数为N，陷阱状态梯度值为G，已标记陷阱区域状态值为：

步骤3搜索陷阱起始顶点。从坐标原点沿X正方向进行层内搜索，沿Y方向进行层级搜索，每次移动1个栅格，判断当前栅格状态值V([x,y])，左侧栅格状态值V([x-1,y])，上侧栅格状态值V([x,y-1])，如果满足：

即当前栅格上侧和左侧均为障碍物，且当前栅格为非障碍物，则认为当前栅格为陷阱区域的起始顶点，将疑似陷阱标志位置1，将当前层疑似陷阱序号加1，记录当前坐标，转步骤4；否则不做任何处理，继续搜索起始顶点。

步骤4继续沿X右侧移动，判断V([x,y]),V([x,y-1]),V([x,y+d]),V([x+1,y]),若V([x,y-1])＞0,则此处非陷阱区域，置0疑似陷阱标志位，返回步骤3；若V([x,y+d])=-A，为防止将可行路径识别为陷阱区域而变成不可行域，则认为[x,y+d]为当前疑似陷阱非相邻障碍物，取消当前层的疑似陷阱标志位，返回步骤3，其中d为可行路径宽度调节参数。若同时满足：

即当前栅格处于疑似陷阱，累积当前疑似陷阱中的栅格长度，根据上一层V([x,y-1])的值来判断当前栅格处于陷阱中的位置，然后转步骤5：

图2 栅格地图陷阱搜索流程图

若未能满足上述不等式，则将当前疑似陷阱排除，清除陷阱栅格长度和所处层级位置，清除疑似陷阱标志位，返回步骤3。

步骤5当沿着当前层疑似陷阱搜索至另一端顶点时，即：

判断目标位置是否处于当前层陷阱中，如果否，则记录陷阱序号、起始顶点坐标及陷阱长度。如果目标位置处于陷阱当中，则将当前疑似陷阱排除，清除陷阱栅格长度和所处层级位置，清除疑似陷阱标志位，返回步骤3。

步骤6当一层搜索结束时，根据当前层记录的陷阱个数、陷阱序号及每个陷阱的长度来更新相应位置的值函数V，并从y+1层再次进行步骤3，直至遍历整个栅格地图。

步骤7完成一次遍历之后，再分别沿X正方向进行层内搜索，Y负方向进行层级搜索；沿Y正方向进行层内搜索，X正方向进行层级搜索；沿Y正方向进行层内搜索，X负方向进行层级搜索；经过4次栅格遍历，能发现不同朝向的凹形陷阱。

步骤8更新完所有陷阱区域的状态值函数后，根据当前状态-动作对(S,a)来更新Q值，即采取动作a后所获得的瞬时回报值加上当前状态的最大折扣累积回报V(S)：

如图2所示为示例栅格地图的陷阱搜索过程，其中绿色栅格代表疑似陷阱起始顶点，黄色栅格代表疑似陷阱栅格，蓝色代表疑似陷阱结束顶点，红色代表疑似陷阱取消栅格，灰色代表已确认陷阱栅格(d=1)。如图3为陷阱搜索结束后各栅格的状态值，陷阱区域状态值呈现梯度变化。

图3 栅格地图陷阱搜索完成后状态值

初始化完成之后，环境地图状态-动作值函数有充分的环境先验信息，采取无障碍物试错的贪心策略。

回报函数是智能体移动行为的判断准则，获得回报越大，则相应的行为策略概率得到提高，回报值越小，则对应的行为策略概率减小。基于Q-learning的常规路径规划把到达目标点的回报值设为正数，激励朝目标方向移动的行为策略，把碰到障碍物的回报值设为负数以惩罚相应的行为。因此，基于此类的路径规划方法是从无任何环境认知的状态进行不断的试错，最终收敛Q值查询表，使智能体以最优的路径达到目标点[15]。

这样的试错策略难以应用到真实的环境中去，对于真实的移动机器人，如果采用无环境先验信息的试错学习，会不可避免地撞上障碍物，直接损坏本体，无法进行后续实验。因此对状态-动作值函数表的更新进行如下假设：当智能体在随机探索下预测动作a的下一个环境状态为障碍物，直接取对应，并按照策略进行下一步动作选择，由于规定了可探索环境模型的Q(S,a)≥0，每次检测到障碍物后，将其从可探索环境模型中剔除，在避免了障碍物碰撞的同时，减少了可迭代Q值查询表，能有效加快收敛速度，并能应用于真实未知环境中的路径规划，无需对障碍物设定回报函数值。

5 仿真实验

采用python编程环境，pygame模块作为地图绘制工具进行未知环境下的复杂地图路径规划算法验证。建立地图模型尺寸为800×500，最小移动单位为5，智能体动作空间集合A(s)包含前进、后退、左移、右移、左前移、右前移、左后移、右后移8个动作，动作空间集A(s)越大，对应的路径轨迹越平滑。将地图划分为160×100个网格作为环境状态空间S。以环境地图的左上角为坐标原点，水平方向为X轴，竖直方向为Y轴建立坐标系，设定起始点和目标点位置如图4所示：绿点代表初始点，初始坐标为（760，200），蓝点代表目标位置，目标坐标为（100，60）。

图4 环境地图、起始点与目标点坐标位置示意

在确定起始点和目标点坐标之后，进行引力势场和陷阱搜索初始化Q值函数，将环境的已知信息更新于Q值表之中。图5所示为进行陷阱搜索之后的环境状态，其中绿色线条所在区域为陷阱区域，黑色区域为有效探索空间，相比于初始化之前减小了有效状态空间。其中2号、5号陷阱至外部障碍物之间的距离d由参数调节。

图5 陷阱区域

为了验证本文提出方案的有效性，在同一环境地图下进行3组对比实验，分别采用常规的不带有环境先验信息的Q-learning算法、只应用引力势场作为环境先验信息的Q-learning算法和同时应用引力势场和陷阱搜索作为环境先验信息的改进Q-learning算法进行路径规划，采用相同的折扣率、学习率和ε-greedy法则，每种方法进行2000次迭代，得到最终路径和起始位置到目标点所需的步数。

通过仿真实验发现，没有任何环境先验信息的强化学习路径规划在设定的复杂环境地图中无法顺利到达终点，第一次迭代经过100000步的移动仍然未能到达目标点，即认为在无环境先验信息且移动路径不能穿越障碍物的情况下，基于Q-learning的强化学习算法的路径规划难以达到目标点，无法完成规划。

其余两组方法均能从起始位置到达目标位置，但加入陷阱搜索去掉了较大范围的路径搜索，迭代速度明显快于未加入陷阱搜索的算法，且在初始的若干次迭代过程中，从起始位置到达目标位置所需的步数更少，用时更快。其部分训练代数路径规划效果如图6和图7所示，相同的训练次数图7的移动路径优于图6所示路径，基于陷阱搜索的环境先验信息使得智能体在整个训练过程中不会移动至陷阱区域，提高了算法的效率。

图6 基于引力势场的强化学习路径规划

将这两种方法的训练次数作为横坐标，每次迭代从起始点到终点所需移动的步数作为纵坐标做图可得这两种方法的训练速度和训练效果，迭代收敛趋势如图8所示。由图8可知，进行陷阱搜索作为环境先验信息的路径规划训练效果明显优于未进行陷阱搜索的路径规划，前者收敛速度更快，且在相同的训练次数下得到的移动路径短于后者，整个训练周期时间更短。

6 结论

图7 基于引力势场和陷阱搜索的强化学习路径规划

图8 有无陷阱搜索对路径规划迭代影响趋势图

传统强化学习由于训练速度慢，迭代效率低而难以直接应用。将引力势场和陷阱搜索联合作为环境先验信息初始化Q值函数的强化学习路径规划可以得到更快的收敛速度和更优的移动路径，同时利用初始化避免对障碍物的试错探索减少了移动体有效状态空间，在明显少于传统强化学习的训练次数情况下达到更好的路径搜索效果。对于较为复杂，凹形障碍物较多的环境，传统的路径规划算法不仅计算量庞大，而且易陷入局部陷阱中无法逃逸，本文提出的算法针对此类环境有较高的规划效率，能找到较优的路径。