地下结构抗震设计的等效地震荷载动力有限元方法

吴 敏

(上海市城市建设设计研究总院(集团)有限公司， 200125， 上海//工程师)

随着我国基础建设的大力发展，城市地下空间被大量开发和利用。长期以来，人们普遍认为地下结构抗震性能优于地面结构[1]。直到1995年日本阪神大地震中，大开站等地下结构遭受严重震害，地下结构抗震设计才逐渐引起工程设计人员的重视。

目前，简化抗震设计方法依然是工程设计人员进行地下结构抗震设计的主要手段。而开展简化抗震设计的第一步是计算等效地震荷载，即进行土层地震反应分析。过去，人们开发出了等效线性化程序(如经典的Shake91)进行一维土层地震反应分析。研究表明，等效线性化方法不能反应土层真实的运动过程，在输入地震动强度较大时，计算误差较大，甚至还可能出现死循环现象[2]。此外，笔者通过长期实践发现，与动力时程法相比，采用等效线性化程序计算所得等效地震荷载进行抗震分析时，所得的结构内力总是偏小，等效线性化方法的准确性受到质疑。如今，有限元方法广为人知。《城市轨道交通结构抗震设计规范》[3](GB 50909—2014)中指出，动力有限元方法可以用于自由场的地震反应分析，但缺乏具体要求。人们对于如何准确采用动力有限元方法进行土层地震反应分析知之甚少。

本文以上海某地下结构为工程依托，采用大型通用有限元软件ABAQUS进行二维自由场地震反应分析，详细介绍了建模过程及其要点，并以传统等效线性化程序EduShake为对照，验证了该方法的有效性。对于从事地下结构抗震的工程设计人员及相关学者具有指导意义。

1 等效地震荷载

简化抗震设计方法的基本思想是：地下结构受到周围土层的约束，而地层在地震作用下存在峰值响应，在该响应下结构的内力响应也最大。因此，多数简化抗震设计方法本质上是通过计算自由场在地震作用下的动力响应，从而选取合适的力或位移形式的最不利地层响应作为等效地震荷载，再通过静力的方式计算结构在地震作用下的真实受力情况。可见，等效地震荷载将复杂的结构动力问题转化为易于计算且能满足工程设计需求的静力问题。

表1列举了目前我国规范或学术界讨论较多的几种地下结构简化抗震设计方法及其采用的等效地震荷载形式。基于土层位移和土层加速度2个主要方向的研究，均已研究出了多种简化抗震设计方法。

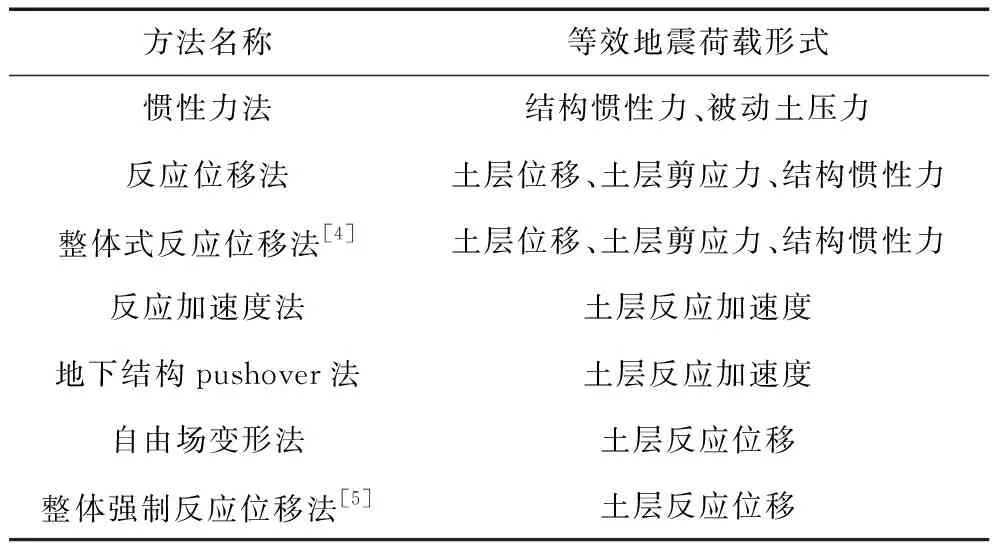
表1 常见地下结构简化抗震设计方法及其等效地震荷载

2 运用动力有限元求解等效地震荷载

2.1 计算模型

以上海某地下结构所在地质断面为例，运用大型通用有限元软件ABAQUS，建立长为500 m、高为60.5m的二维平面应变模型。经过对比，本文未采用无限元边界，而以中间密两侧疏的网格划分方式来减小地震波在边界处的激荡效应。根据ABAQUS软件帮助文档，无限元对于水平入射的地震波的吸收作用有限甚至会引起震荡。模型中土体采用平面四节点单元(CPE4R)，本构模型采用摩尔库伦模型。场地自重应力采用ABAQUS软件的自动地应力平衡技术来模拟，自由场平衡后的土层变形可达到10-6m。

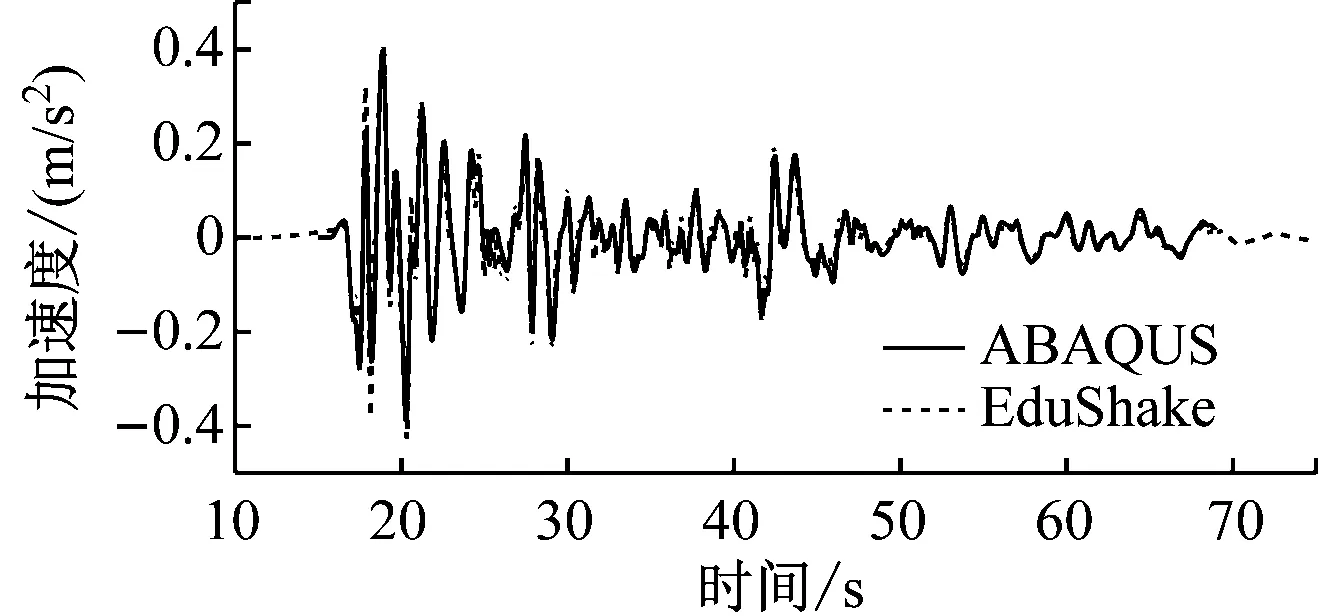
在对照组EduShake软件中建立相同的土层模型，土体的非线性动力特性采用程序中Sun等建议的黏土曲线。地震波选择常用的El-centro波。EduShake软件在计算过程中会自动滤除频率大于20 Hz的地震波成分，所以对于输入ABAQUS软件的地震波需做同样的滤波处理。处理后的El-centro波时程曲线如图1所示，计算时将峰值加速度调幅至0.1g后沿模型底部水平输入。

图1 El-centro波时程曲线

2.2 关键参数

土层动力非线性问题是采用ABAQUS软件进行自由场地震反应分析的要点。ABAQUS软件中，土体动力非线性本构模型的建立需要二次开发，较为复杂。因此，文献[6]以等效线性化程序计算反馈出的等效剪切模量及等效阻尼比来近似考虑该问题。

等效剪切模量可以换算为弹性模量输入土层摩尔库伦模型中，土层阻尼可通过定义材料瑞丽阻尼来实现。首先采用ABAQUS软件线性慑动分析步对场地进行模态分析，计算得出工程场地的前两阶阵型频率f1=0.321 Hz，f2=0.865 Hz。再通过公式(1)即可计算得出瑞丽阻尼中的α系数和β系数。

式中：

ξ——等效阻尼比。

最终，ABAQUS软件自由场动力时程分析中土层的物理力学参数如表2所示。

2.3 结果对比

本节从单点对比、最不利时刻土层侧移曲线及加速度曲线对比两个角度，比较了ABAQUS软件动力时程分析与等效线性化程序EduShake软件的计算结果，从而验证动力有限元计算的有效性。

2.3.1 单点对比

通常，地震波在向上传播的过程中具有明显的放大效应，模型上部的土层加速度响应、位移响应最大。在模型的顶部与中部分别选取2个单元节点，其中顶部位置与中间位置的加速度响应、位移响应对比分别如图2、图3所示。从图中可以看出，

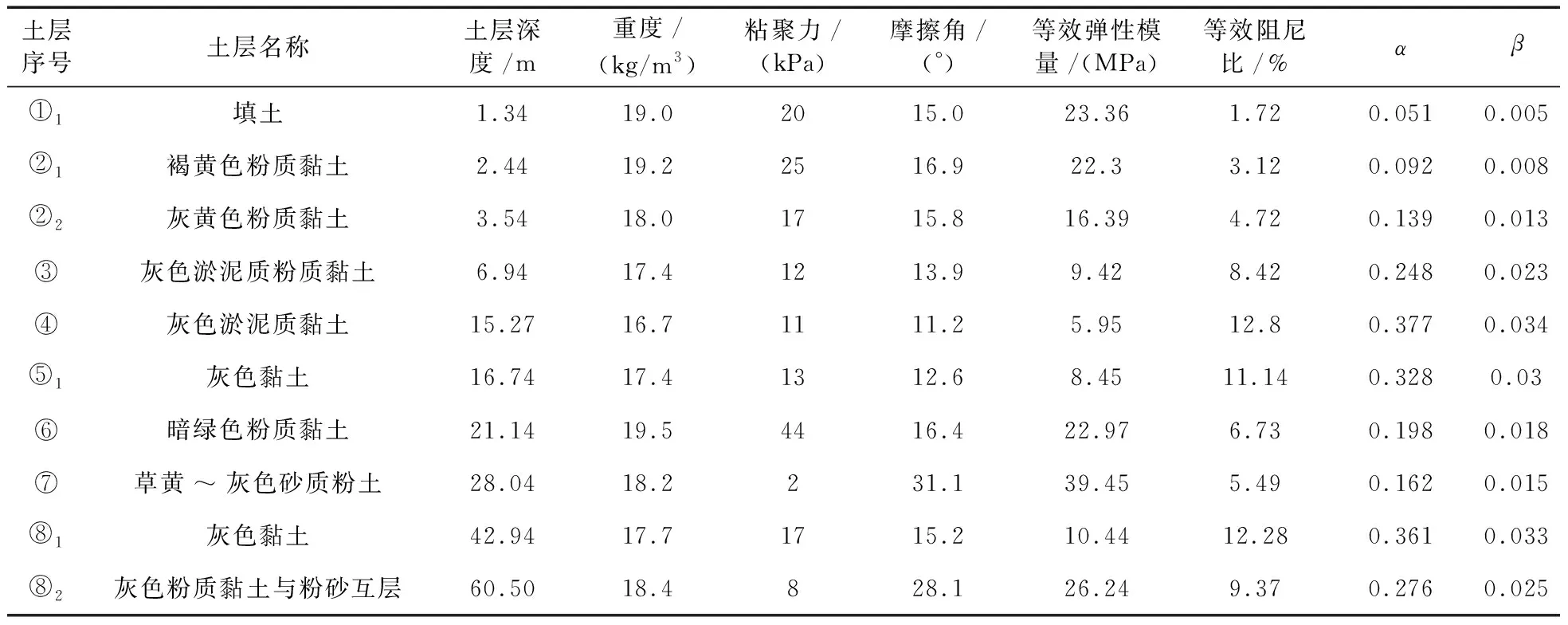
表2 ABAQUS软件中输入的土层参数

ABAQUS软件计算所得土层在地震作用下的加速度响应与EduShake软件的计算结果基本吻合，顶部峰值加速度误差仅为1.58%，而腰部峰值加速度误差为1.72%；水平位移时程曲线总体上基本吻合，顶部峰值侧移误差为6.07%，腰部峰值侧移误差为9.49%。这验证了本文运用动力有限元ABAQUS软件进行自由场地震反应分析的有效性与正确性。

a) 土层加速度时程

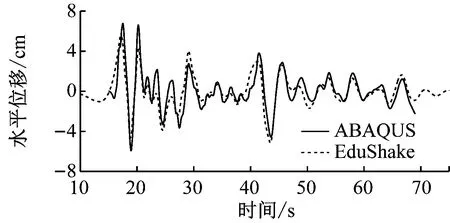
b) 土层位移时程图2 模型顶部动力响应对比图

2.3.2 最不利时刻分布曲线对比

地下结构在地震波的作用下，总会达到某一个最不利时刻，该瞬时结构的侧向变形最大，结构动力响应也最大。该车站结构埋深约3 m，结构高度约为10 m，计算自由场模型中结构顶底板位置处的土层水平位移差，取其峰值位移差所对应的时刻为该结构的最不利时刻。本例最不利时刻为17.6 s，该时刻土层反应加速度与反应位移沿深度的分布曲线如图4所示。总体来讲，ABAQUS软件与EduShake软件的计算结果仍基本吻合，但是误差相对单点对比时明显增大。土层反应加速度的平均计算误差为25.9%，土层位移的平均计算误差为19.4%。误差增大是由这两个分析过程的相位差积累造成的。同时，图4显示出浅层土层对地震加速度具有明显的放大作用，但是浅层的峰值加速度不一定大于更深层土层的峰值加速度，这与浅层地下结构震害明显大于深层地下结构的现象相违背。因而，完全基于结构惯性力所建立的地下结构简化抗震设计方法惯性力法已被《城市轨道交通结构抗震设计规范》(GB 50909—2014)等规范淘汰[4]。相反，在地震作用下土层反应位移的分布曲线规律较明显，基本呈现倒三角型，所以某些学者抓住该特点提出了更为优化的地下结构简化抗震设计方法——整体强制反应位移法[5]。

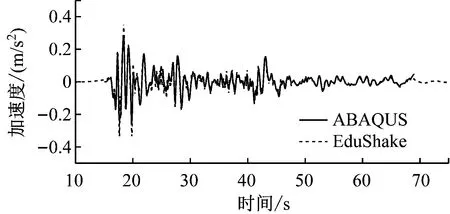
a) 土层加速度时程

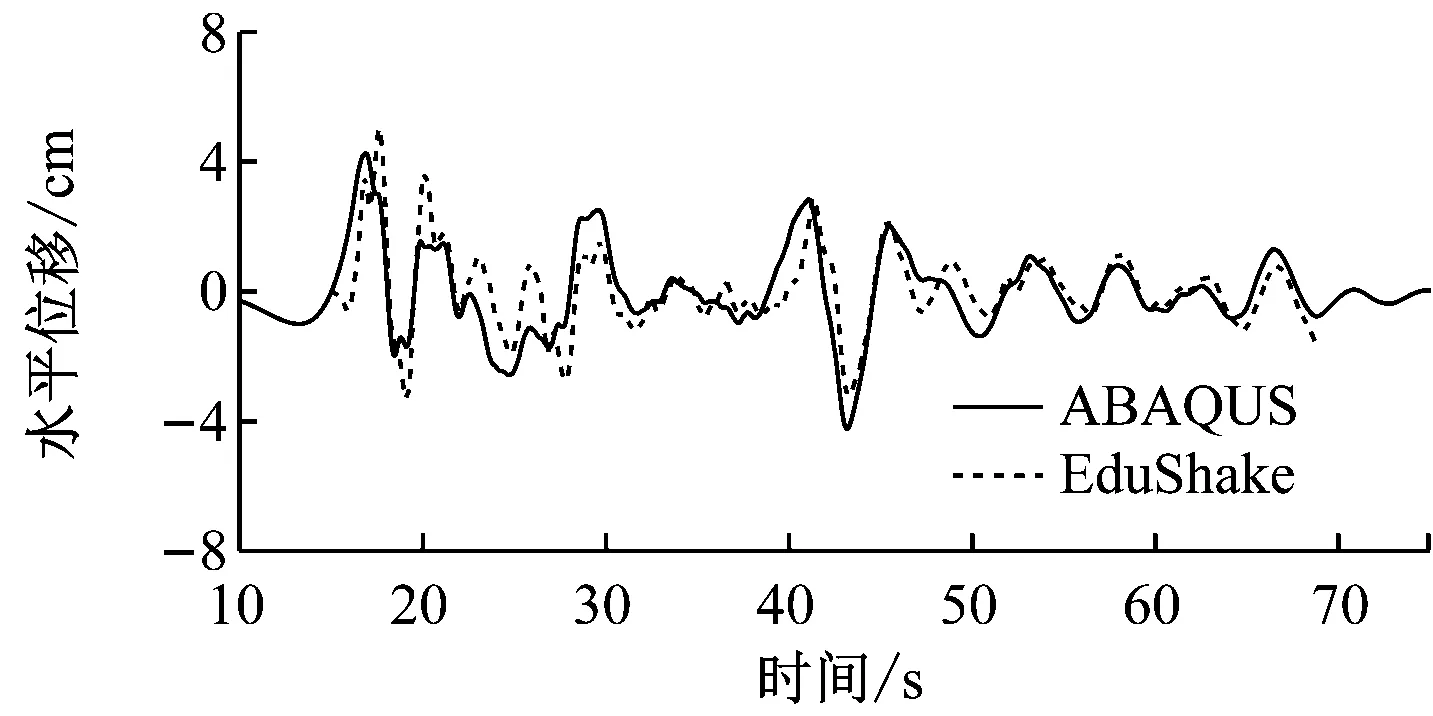
b) 土层位移时程图3 模型中部动力响应对比图

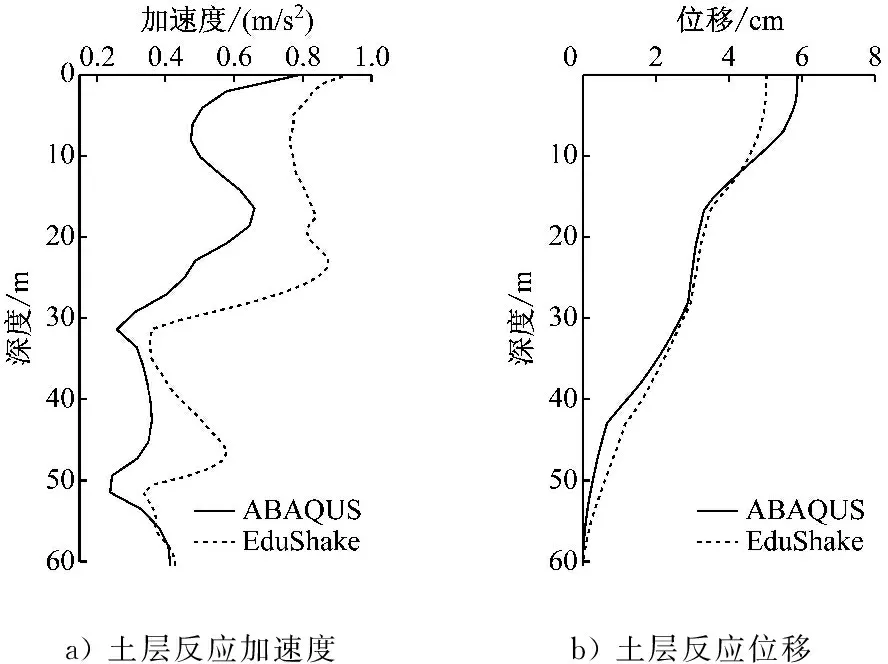
a) 土层反应加速度b) 土层反应位移

图4 最不利时刻土层反应沿深度的分布曲线

3 结语

本文基于大型通用有限元软件ABAQUS，以动力有限元方法开展了地下结构简化抗震设计中等效地震荷载的数值模拟，并将其计算结果与传统的等效线性化程序EduShake软件的计算结果作对比，得出以下成果：

(1) 动力有限元法计算所得的单点加速度时程曲线、位移时程曲线与EduShake软件计算的结果相比，偏差较小；最不利时刻的加速度与位移沿深度的分布曲线偏差相对较大，但曲线走势基本相同。

(2) 考虑土层等效剪切模量与阻尼之后，ABAQUS软件计算所得的土层地震反应与EduShake软件的计算结果基本吻合，验证了该方法在等效地震荷载计算中的有效性与正确性。

(3) 以动力有限元法进行二维土层地震反应分析更为直观、简便，其丰富的后处理方式也有利于设计人员展开抗震研究及工程设计。