山区桥梁超高墩日照温度效应数值分析

林国涛， 苏 波

(中交公路规划设计院有限公司， 北京 100088)

近年来，高速公路以及铁路的建设发展迅速，公路及铁路线往往会经过一些深山峡谷，由于高墩大跨桥梁的诸多优点，高墩得到了大量的运用。

但是高墩对外界环境温度敏感。太阳东升西落使得桥墩的迎阳面和背阳面温度、桥墩内外温度均有所不同。温差的存在会使得高墩结构产生较大应力和变形，例如位于重庆的高240 m的烟囱，跨越通惠河的高墩大跨连续箱梁都由于日照而出现多处裂缝[1]，因而对高墩的日照温度场和温度效应的研究显得十分重要。对此，国内外研究人员进行了一系列的试验及理论研究。

在温度场分布方面，前人通过观测和试验，测定了混凝土结构的温度分布，证实了在空心桥墩中存在相当大的温差[2]；Emerson基于气候参数与混凝土热运动的试验，指出太阳辐射是最重要的影响因素[3,4]；Stephenson用指数函数来分析混凝土结构沿壁板厚度方向的温度分布，Zuk利用气象资料，指出气温、风、太阳辐射和材料都会影响桥梁的温度分布[5]；武立群、陈泗瑶等基于实测和有限元仿真提出了桥址的温差曲线[6,7]。

对于温度效应，Fritz Leonhardt定量地讨论了厚壁箱梁的温度应力问题，认为预应力箱梁产生裂缝的主要原因是温度应力[2]；Priestley基于两个基本假设，给出了温度应力的解析公式，将温度应力分为温度自应力和温度次应力两部分[8,9]；刘兴法、管敏鑫等学者，基于对桥梁的温度观测数据，得出了温度应力的计算公式；张运波对八边形和双肢薄壁高墩温度效应及稳定性做了较为完善的叙述[10]。

前人的大多数研究都是基于普通混凝土结构，对高墩结构复杂细致的温度效应的研究较少。故对高墩温度效应的研究具有很高的价值。

本文做了如下工作：基于新庄特大桥工程，采集现场所需参数，根据太阳辐射相关理论，利用MATLAB求解三腔与双肢组合高墩的内外温度，再运用ANSYS建立高墩模型，做瞬态分析求解高墩的温度场，将温度场施加在模型上，求出结构的温度效应，选取其中最不利情况做分析，作为控制指标，为实际工程的施工提供参考。

1 工程概况

新庄特大桥为华坪至丽江高速公路的一座大桥，为高墩大跨结构，位于新庄乡新庄村，当地经纬度为101.20°E，26.59°N。该桥梁跨U型沟谷，两侧山坡较陡，谷底地势平坦，最大桥面高度181 m。路线为分离式布置，新庄特大桥的主墩及过渡墩墩身采用 C50 混凝土；引桥空心墩墩身采用 C40 混凝土。

主桥高墩截面形式为三腔截面和双肢截面的组合，对于165 m的高墩，底部实心部分为6 m，其中下部的三腔截面高度范围为89 m，上部的双肢截面的高度范围为70 m。此主墩的两个截面的尺寸分别见图1，2。

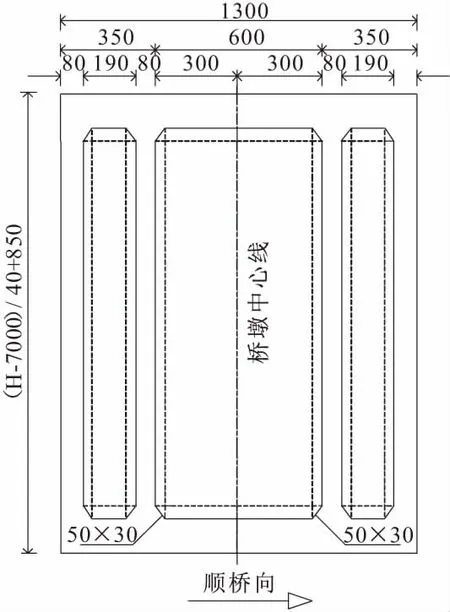
图1 三腔截面/cm

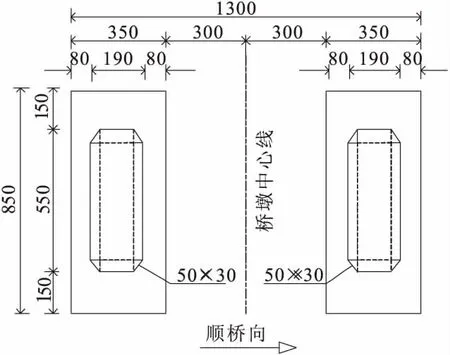
图2 双肢截面/cm

上部主梁及下部桥墩混凝土容重取用26 kN/m3。桥位区最热日平均气温取34℃，最冷日平均气温取0℃。

对于桥梁走向，以右幅路为例，其道路中心线如图3所示，各个面的法线方向与正南方向的夹角为方位角，三腔墩各表面的方位角如表1所示(双肢墩方位角类似)。

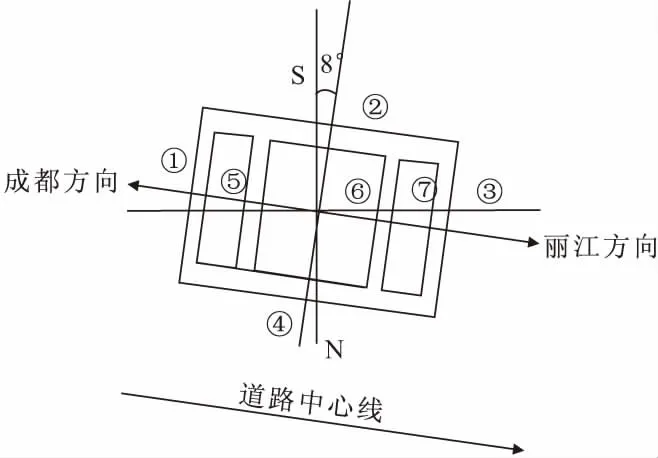
图3 路基典型右半断面图

表1 桥墩各表面方位角

注：(1)方位角以正南为0°，偏东为负，偏西为正；(2) ⑤，⑥，⑦分别为三个空腔的内壁四个面，不存在方位角，亦不存在太阳辐射，统一取外界气温的修正值(幅值有所变化，相位有所落后)

2 高墩综合气温计算

高墩的温度场与其地理位置、方位角、太阳辐射强度、风速、周围环境密切相关。其中，太阳辐射是一个很重要的影响因素。

2.1 太阳辐射强度的计算

太阳辐射对结构的影响，总体上可以分为太阳直接辐射、天空辐射、太阳辐射和天空辐射的反射、大气逆辐射、地表环境的辐射与大气逆辐射的反射五项，各项算法如下[11]：

(1)太阳直接辐射

(1)

(2)天空辐射

(2)

(3)太阳辐射和天空辐射的反射

(3)

式中：ruk为地面环境短波反射系数，也称反射率，以%计。

(4)大气逆辐射

(4)

式中：CS为黑体辐射系数，其取值为CS=5.775×10-4W/(m2K4) ；TA为外界气温。

(5)地表环境的辐射与大气逆辐射

(5)

式中：U为地表环境总辐射强度；Ra为大气逆辐射引起的反射的强度。

基于该项工程，取相关参数进行分析，具体参数如下：地理坐标为101°E，27°N，计算日期取夏至日，为保守考虑，当日最高气温取为34℃，当日最低气温0℃，最高气温出现时间为下午2∶30，天气晴朗微风(风速为3 m/s)。有了这些参数，则可以求出太阳辐射强度。

2.2 综合气温的计算

空心墩与外界发生热交换主要是通过对流、吸收太阳辐射能量和热辐射三种形式。其中，对流荷载在 ANSYS 中施加最为简便，将太阳辐射和热辐射也转换成对流来施加能够简化工作。受到太阳辐射的薄壁空心墩边界与外界空气有对流换热，把太阳辐射引起的热流密度换算到气温中来考虑太阳辐射和热辐射的影响，得到综合气温：

(6)

式中：Tsa为综合气温(℃)；at为吸收率；I为太阳辐射强度(W/m2)；hc为综合热交换系数(W/(m2·℃))，考虑了太阳辐射和热辐射，与风速有关。

这里将太阳辐射强度、热辐射和对流三种荷载用对流来代替施加。将综合热交换系数hc、综合气温Tsa赋给边界上的节点。

求解综合温度时，需要知道吸收率和综合热交换系数。对于混凝土结构温度场分析和温度效应计算，常取吸收率at=0.65[12]；微风风速v=3 m/s，根据式(7)[13]取得综合换热系数为 22.46 W/(m2·℃)。

hc=12.47+3.33v

(7)

3 温度效应计算

通过前面的工作，我们得到了桥墩内外表面的综合气温，这一节进行温度场及温度效应的求解。温度效应计算的整体思路为：利用ANSYS15.0进行结构建模，选用相应的温度场单元(如PLANE77)进行结构的网络划分，考虑精度和运算简便的要求，划分的尺寸为0.4 m；给定边界条件进行瞬态热分析，初始条件定为稳态分析后的温度，得到模型随时间变化的温度场；不改变节点和单元网格划分，将温度单元转换为结构单元(若是PLANE77则转化为PLANE82，转换的原则要求两种单元在单元形状、节点数目以及插值函数阶次上一致)，然后给定应力问题的边界条件，将所求温度场作为荷载(ANSYS的热-结构耦合功能)施加在模型上得到温度效应结果。

在针对这个项目中的具体问题建模之前，我们按照前人做的一些工作，比较了一下同高度同温度场不同壁厚的空心矩形截面的最大挠度。求得较薄壁空心矩形截面的最大挠度DMX=3.32×10-2m，而较厚壁空心矩形截面的最大挠度DMX=2.77×10-2m。两种截面各时刻的最大位移分别如图4，5所示。

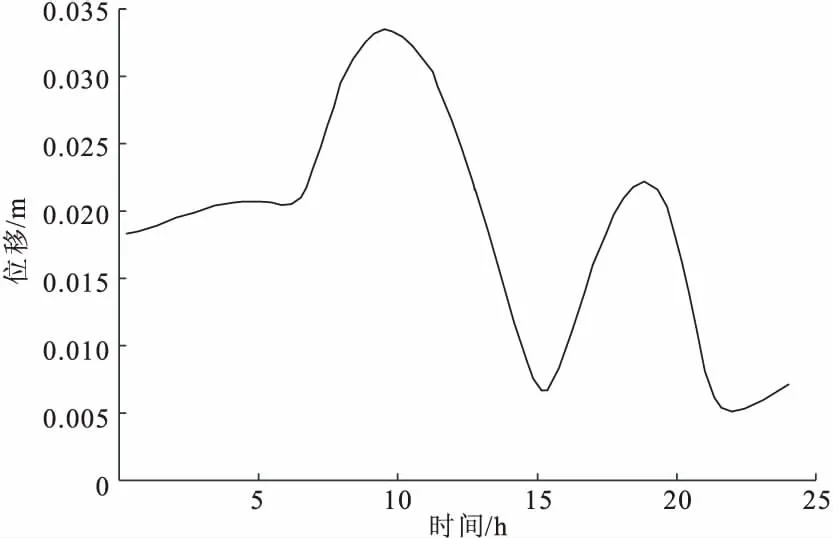
图4 薄壁空心矩形截面各时刻最大位移

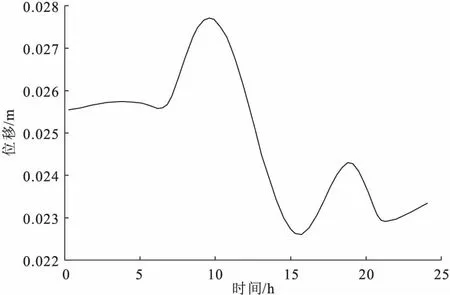
图5 厚壁空心矩形截面各时刻最大位移

从计算结果可以看出，墩壁越厚，空心矩形截面在温度影响下计算出的挠度越小。因此，将实心截面简化为空心截面或者三腔截面去计算，所得的挠度会偏大，这是有利于设计的。本项目中165 m的高墩中实心截面仅有6 m，将实心截面部分等效为三腔空心截面带来的误差不会太大，且偏于保守；因此，我们可以对模型进行简化，用三腔截面代替底部存在的实心截面。简化之后高墩仅存在两种截面计算，即三腔截面和双肢截面，三腔截面的高度范围为95 m，双肢截面的高度范围为70 m。

利用ANSYS15.0进行建模分析，建立三腔截面的模型如图6所示，双肢截面如图7所示。

在计算空心墩的温差应力时，为了方便起见，利用到了Beam189单元。将温度单元PLANE77转换为结构单元PLANE82后，将定义的平面保存为截面文件，再利用Beam189单元进行计算。原因是Beam189单元具备两个很重要的特性，一个是求解的截面应力包含温度自应力和温度次应力，另一个是该单元可以在截面单元上定义不同的材料属性；第二个特性可以便于加载沿截面方向变化的温度荷载。

故可以这样简化加载：保持温度荷载一定，而单元的材料属性沿截面方向变化。例如，真实的情况是温度沿截面线性变化，材料热膨胀系数沿截面不变；则可以取材料热膨胀系数沿截面进行相应的线性变化，而温度取恒定值。

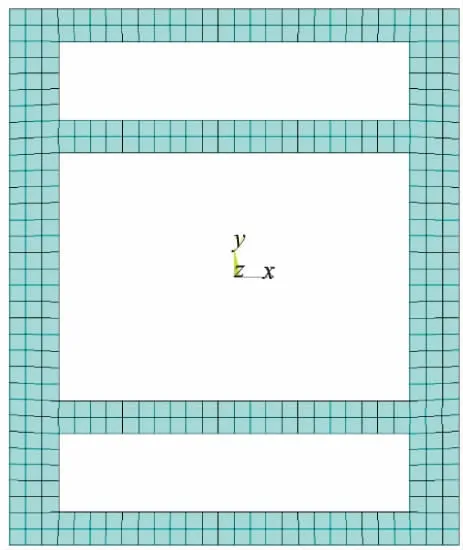
图6 三腔截面模型

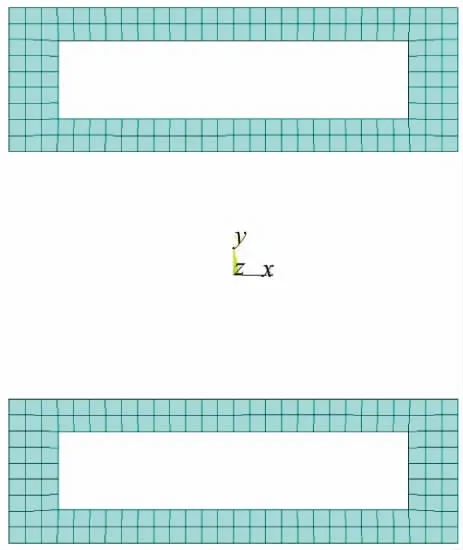
图7 双肢截面模型

4 位移时程分析

按照前面的方法，我们可以计算出三腔与双肢组合高墩的温度场和温度效应。

取165 m三腔截面和双肢截面高墩分别计算得到各时刻最大位移；取95 m三腔与70 m双肢组合高墩进行计算，得到各时刻最大位移；将三种高墩的最大位移绘在同一个时程图中，见图8。由此我们可以得到以下结果：

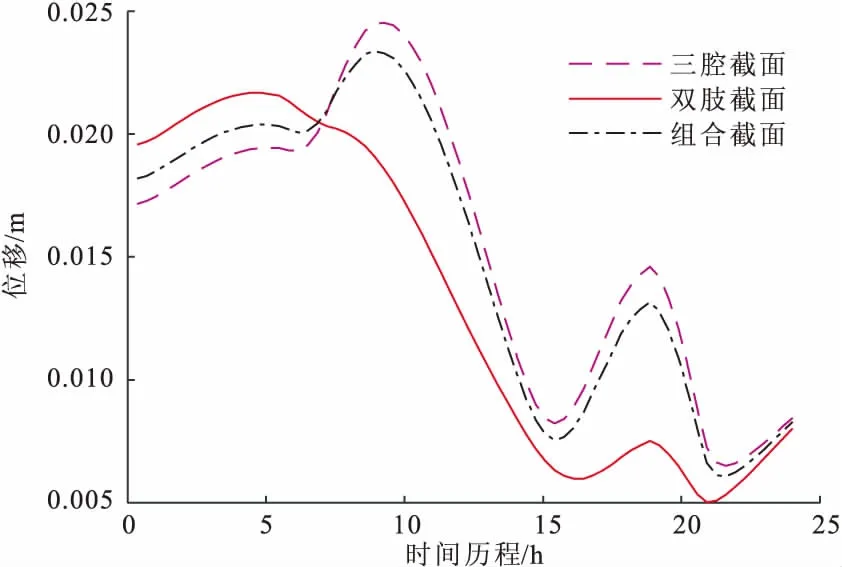
图8 三种截面各时刻最大位移对比

(1)在一整天中，三腔截面高墩的位移最大，双肢截面高墩的位移最小，而三腔与双肢组合截面高墩的位移始终介于两者之间，这种结果是合理的。

(2)组合截面由日照温度产生的位移响应最大值为2.337 cm，这个值比较大，在实际工程中是不容忽视的，也显示出研究的意义。

(3)在该参数取值下，组合高墩的最大位移出现在上午10点左右，原因是此时外界的温度已经较高，而内腔气温还是保持较低状态，导致内外温差很大，从而出现了最大位移。

(4)大约在下午15点，最大位移时程曲线出现了一次极小值，为解释这种现象，我们将外界气温和空腔内壁气温绘制于时程曲线图9中，可以看到，15点前，外界气温开始下降，而内腔气温依然在上升，这导致内外的气温差减小，温差产生的位移也就会减小，故出现了极小值。以此类推，其他极值的出现也可以类似地进行分析。

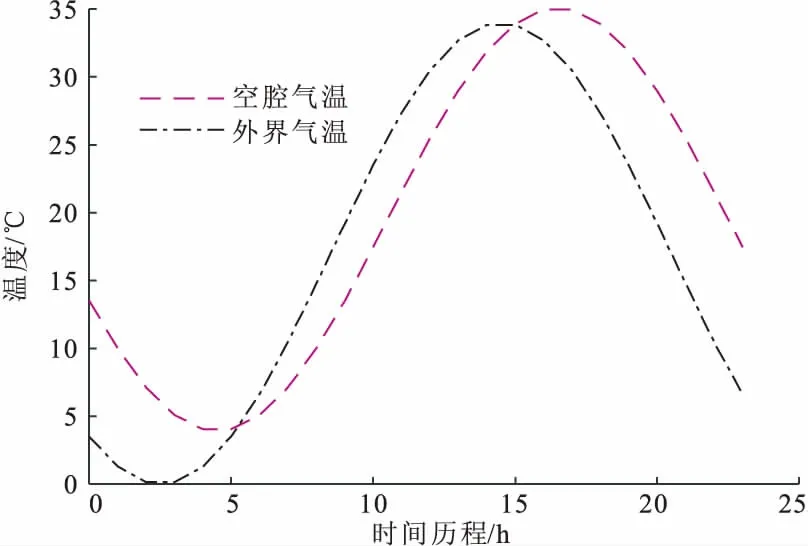
图9 外界与空腔气温时程变化曲线

5 结 论

本文基于新庄特大桥工程，根据相关理论，求解三腔与双肢组合高墩的内外温度，再运用ANSYS建立高墩模型，求解结构的温度场和温度效应。基于结果绘制了165 m高墩在日照影响下的位移时程曲线，得到了以下结论：

(1)同一温度场下，三腔截面高墩的位移响应最大，双肢截面高墩的位移响应最小，而三腔与双肢组合截面高墩的位移响应始终介于两者之间。

(2)日照温度产生的位移响应的大小与变化规律和日气温变化过程密切相关，原因是与高墩内外温差的大小与变化规律相关：温差越大，位移响应也就越明显；温差越小，位移响应也就越小。

(3)对于高墩来说，尤其是地处日温差较大地区的高墩，温差产生的影响十分明显，是不容忽视的。