预应力钢筋混凝土箱梁的结构冗余度

康峰沂

（南通市公路管理处，江苏 南通 226001）

0 引言

高速公路桥梁结构的设计和荷载评估传统上是基于构件的设计。然而在桥梁面临倒塌的危险而采取补救措施前，通常希望桥梁能够有足够的结构冗余度来继续承受主要构件破坏后的荷载[1]，并能有足够的时间撤离并避免人员的伤亡。然而，冗余度的量化并没有完全体现在现行桥梁标准和规程中。美国1985年发表的《结构冗余系统的当前发展状况》[2]提出，尽管已经能够分析得到当承受高荷载时受损和未受损弹性体系的响应，但量化冗余度的研究还很少。因此，为了实现量化冗余度，各种研究和设计规范提出了不同的方法来估计。Dexter在2005年对桥梁冗余度分析做了一个综合的综述[3]。

在最早的设计规范中，AASHTO LRFD[4]提出设计新桥时，采用Frangopol和Nakib的建议在设计检验方程中采用荷载修正的方式。具体地讲，AASHTO LRFD建议采用不同的荷载修正系数0.95，1.00和1.05来反映结构不同的冗余性和柔性。该荷载修正系数综合考虑了结构在预防/安全问题上的重要性。然而，规程并没有解释如何去定义什么样的桥梁拥有高的或低的冗余度和柔性。在AASHTO LRFD的条文说明中提到，冗余度的建议取值在没有特定研究时可以按照经验取值。加拿大规范CAN/CSA-S6-06[5]采用了不同的方法，即直接要求设计师选用不同的抗力系数来反映不同的构件安全度指标，其指标的选取是基于对构件破坏模式和柔性的估计后得到的。类似AASHTO LRFD规范，该方法很大程度上依赖于工程师对桥梁冗余度的确定和构件破坏模式的判断。AASHTO手册中LRFR[6]部分对桥梁评估中采用系统参数放在等式抗力边，当桥梁结构被认定为低冗余度时，其取值范围在0.85到1.0之间。其中表格提供了基于桥梁结构尺寸和外形的系统参数的取值规定。遵循同样的思路，一些额定荷载状态如Florida DOT[7]也提供了一系列系统参数。但正如Mertz[8]所说，这些都是基于有限的分析且很大程度上依赖于“工程判断”。

Ghosn[9]研究了一系列量化桥梁冗余度的方法和标准。很多学者和工程师（如Hunley和Harik,Hovell,以及 Mertz等）、咨询公司（HNTB）和规范编写组织（AASHTO LRFR;Florida DOT;Wisconsin DOT）采纳了NCHRP（美国公路合作研究组织）研究提出的冗余度概念并制定了针对典型的中小跨径桥梁在设计或安全评估阶段的系统参数。然而，NCHRP的研究并没有考虑近些年来较流行的多室箱梁桥型的系统参数。同样，两份报告中也并没有证实他们提供的系统参数能够应用于整个桥梁结构包括上部和下部结构的连接。

本文主要目的在于对近年来应用较多的多箱室桥型提出合理的系统参数。预应力混凝土多箱室因其具有较大的抗扭刚度而广泛应用于弯桥中[10]。本文主要研究了该种桥型的冗余度，并提供给工程师在瞬时横向和竖向荷载下考虑结构冗余度后、可以直接应用的系统参数。

1 桥梁冗余度

图1解释了桥梁结构的性能发展，以及在预测构件安全性、系统安全性和系统冗余度时应当考虑的系统发展水平[11]。荷载增加值LF代表考虑了设计卡车荷载后系统所能达到的不同极限状态。其中，LFu代表整体结构抵抗倾覆的能力，LFf代表功能失效F1代表了第一构件破坏时的状态。

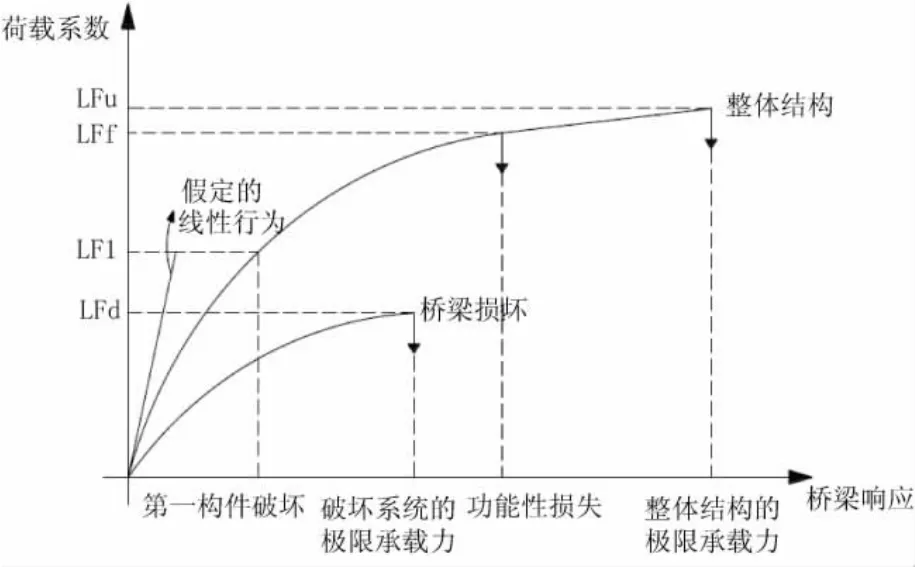
图1 桥梁结构的典型特征

冗余度定义为结构在最主要构件破坏后仍能够继续承受荷载的能力[12]，LFu、LFf、LFd和 LF1之间的比值就可以客观地将结构冗余度数值化。因此，对比最重要构件的承载力，以下三个系数可以定义为与结构冗余度有关的承载力比值。

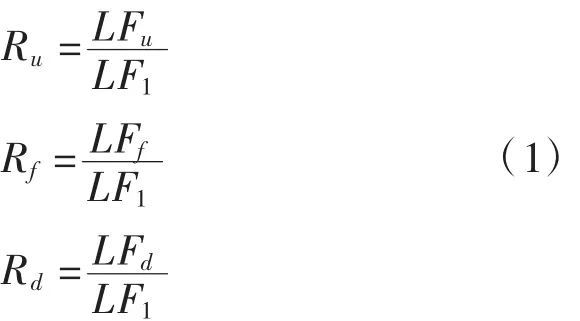
式中：Ru为结构极限状态的储备比值；Rf针对结构功能失效状态的储备比值；Rd是损坏时结构的储备比值。Ru、Rf和Rd就可以作为量化冗余度的方法，来代表结构在最重要构件破坏后所能承受荷载的能力。

2 系统参数

NCHRP的研究提出，在设计/安全检查阶段，

考虑结构的系统冗余度可以采用引入以下参数：

式中：RNn是考虑冗余度后的构件承载力；s是系统参数；是按照现行AASHTO LRFD规范得到的抗力分项系数；γi是荷载的分项系数；Qi是i的荷载效应。

由式（2）得到的系统参数提供了一种计算系统储备能力的方法，这种储备能力与延性、冗余度、结构安全性和它们之间的相互作用有关。还与另外两个参数相关，即su和sd，su代表了在超越整体结构最重要构件强度后系统的功能性和抗倾覆能力，sd为在破坏阶段的强度。功能性是指初始整体结构承受重活载后其竖向位移不超过跨径/100的大小，否则桥梁将不适合继续运营[13]。破坏状态包括了多梁桥中某主梁破坏、某箱梁桥某腹板的破坏或桥墩中某个墩的屈曲等。

3 桥梁概述

图2是一个多室预应力箱梁和2个墩柱的示意图。四室箱梁的顶板宽度为18 m。三跨连续梁总长125.6 m，其跨径分别为38.4 m、51.2 m和36 m。顶板和底板的厚度分别为23 cm和21 cm。梁高为2 m。上部结构与下部结构的连接采用与箱梁高度相同，宽度为2.4 m的横梁连接。梁的下部支撑采用直径1.8 m的圆形墩并通过抵抗力矩的刚性连接。在后面的分析中，不考虑力矩刚性连接的情况同样进行了分析。

图2 桥梁尺寸

混凝土强度取值为28 MPa，钢筋取420 MPa，其极限应力为620 MPa。预应力钢筋其最大应力为1 860 MPa，其屈服应力为1 586 MPa。每个截面的预应力筋面积为0.8361 m2。总的预应力损失计入弹性压缩、徐变、收缩和钢筋松弛等因素后假定为138 MPa。钢筋采用沿主梁抛物线的线形，所有截面的弯矩-曲率计算都包括了钢束的实际位置。

4 侧向静力弹塑性pushover分析

4.1 横梁-墩刚性连接的模型1

原始模型的侧向静力弹塑性pushover分析采用SAP2000。塑性铰的位置设置在墩柱的顶端和底部，为了获取非线性的弯压复合作用，见图3（a）。荷载包括非线性恒载、预应力张拉和活载。图3（b）显示了破坏模式和塑性铰的扩展。恒载的计算按照SAP2000的自重计算，然后将预应力施加到结构上形成成桥结构。

图3 横向Pushover分析

4.2 铰结形式的模型2

模型2将横梁与墩柱采用铰结的形式，其铰接点在墩顶和横梁之间，见图3（c）。采用弹性杆释放墩顶的扭转刚度。破坏模式和塑性铰的扩展见图 3（d）。

墩柱的截面弯曲曲率见图4。受拉区混凝土超过其极限抗拉应变而破坏，受压区混凝土达到其极限抗压应变。桥梁承受20%的HL93荷载，其布置双车道来代表在遭受地震时，桥梁上的交通状况。

图5对比了模型1和模型2的静力弹塑性pushover分析。根据模型1的线弹性分析，第一个构件达到其承载力时施加的横向力大小为P1=2 272 kN，即墩底部达到其抗弯承载力。在塑性pushover分析中，系统的极限承载力为Pu=3 266 kN。根据式（1），模型1的冗余度比值Ru=3266/2 272=1.44。类似的，模型二的冗余度比值Ru=1 565/1 184=1.32，比模型1结果低8.3%。

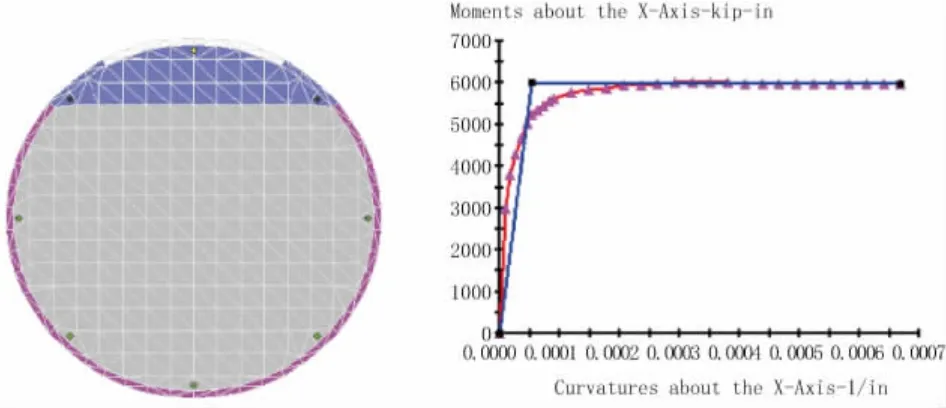
图4 墩柱在DL和20%的HL荷载下截面的力学行为，深蓝色为混凝土受压区

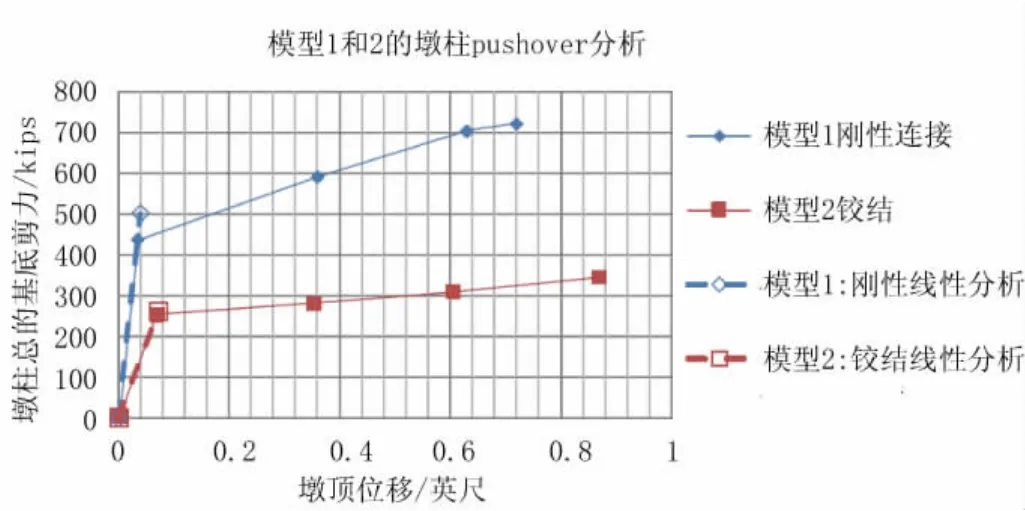
图5 横向Pushover分析

5 竖直非线性Pushdown分析

SAP梁格模型3：竖向荷载下的非线性Pushdown分析并不像模型1和2那样，而需要建立完整的空间模型。箱梁的非线性可以通过塑性铰理论模拟，多箱室梁采用梁格来实现横向和纵向的刚度。梁格弯曲和扭转刚度可通过现有的理论[14]计算得到，该理论经证明可以准确地得到梁的力学特点。两列间距4ft的HS-20卡车荷载施加在中跨，见图6。

图6 两列HS-20卡车荷载下3-D梁格模型和梁格弯矩-曲率曲线

6 SAP和ABAQUS结果对比

本章节主要验证SAP2000建立的梁格模型分析竖向荷载下上部结构的正确性。桥梁上部结构与模型3一致，在SAP2000和ABAQUS中采用铰结支撑简化分析。图7为ABAQUS实体模型，网格划分截面，预应力钢束的布置，钢筋和荷载的布置形式。非线性分析的竖向荷载采用标准的两列HS-20卡车荷载，653 kN。从图8可以看出，梁格分析中得到的极限荷载仅比ABAQUS的结果低6.6%。对比结果可以证明梁格模型可以准确地预测破坏荷载。

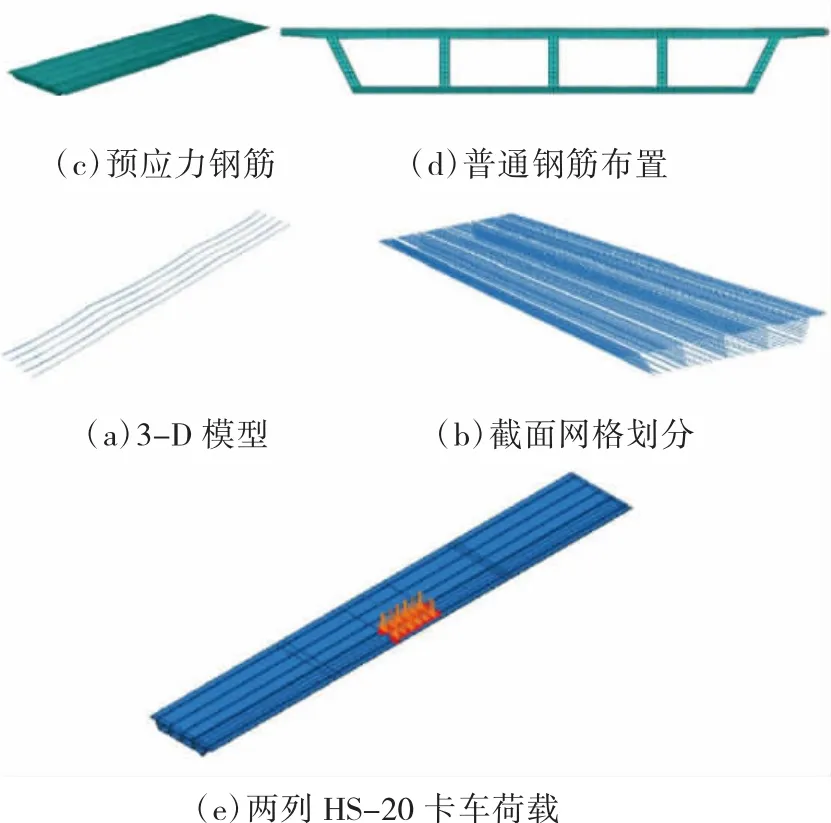
图7 ABAQUS有限元模型

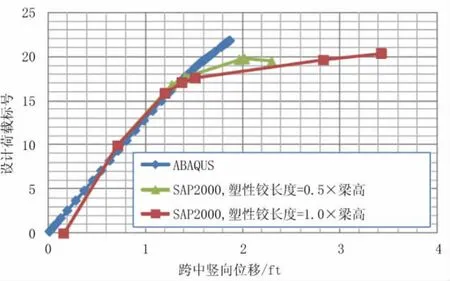
图8 SAP2000分析结果与ABAQUS结果对比

6.1 单根柱破坏的模型4

在模型4中，为了研究一根主要的墩柱发生破坏后系统承受荷载的能力，将一根柱从结构中移除。这种破坏模式在现实中可以是一根墩柱被卡车、轮船或洪水中的巨大碎片冲撞，或一根墩柱的基础遭遇重大冲刷，甚至可以是施工重大过失或一根柱遭受了重大退化。

本章节考虑了两种情况。一种是在模型4-a中柱仅在线弹性范围内，另一种是模型4-b中更实际地考虑上部结构和下部结构的非线性行为。图9对比了模型4-a、模型4-b以及模型3的结果。考虑模型4-a的柱仍处于线弹性范围内，预应力梁表现出很大的冗余度。Model 4-a的破坏发生在外部梁的负弯矩截面，其荷载指标（也叫做设计荷载序号）LFd=23.8。4-a的冗余比值为Rd=23.8/18.0=1.32。模型4-b在非线性 pushdown分析下，当LFd=19.0时，模型4-b达到了其极限承载力，因此冗余比值为Rd=19.0/18.0=1.06。

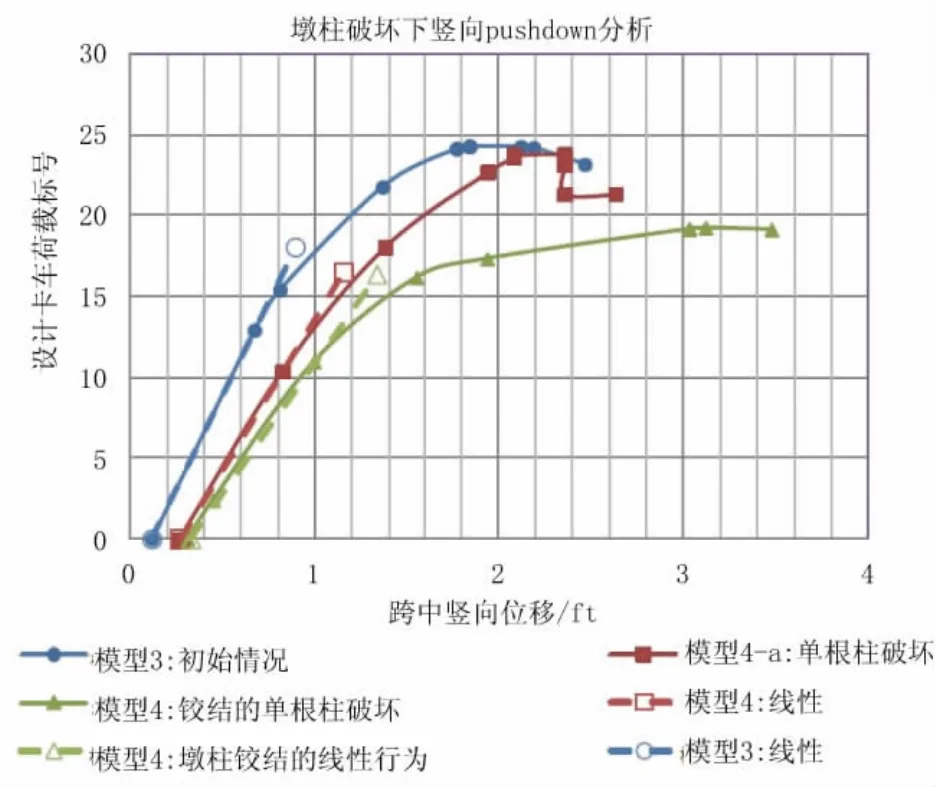
图9 预应力箱梁墩柱移除后结果

6.2 腹板破坏的模型5

另一种破坏模式是考虑一根腹板内预应力钢筋的损坏。这种情况是通过将沿纵向的抗弯刚度设置为0。本例中选择梁格模型中的第二根纵梁作为破坏的梁来模拟最坏的情况，因为根据HS-20卡车荷载在原结构中的布置，第二根纵梁将承受最大的荷载。因为内梁遭受破坏，结构承受偏心荷载时外部的梁将成为最重要的受力构件。图10为模型5的极限承载力，此时总荷载LFd=18.2。因此，结构的冗余比值Rd为18.2/18=1.01。

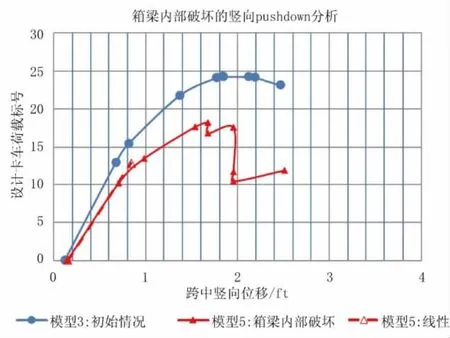
图10 箱梁腹板破坏的pushdown分析

在NCHRP的研究中提到，本文中运用的梁格模型已经被实验所证实，实验分别是由Kurian和Menon做的4根混凝土箱梁模型、Mirra[15]等学者在麦吉尔大学实施的预应力混凝土箱梁和McLean等学者实现的三墩梁桥的弯曲试验。试验结果均证明梁格模型可以用于准确预测混凝土箱梁的极限荷载和墩柱的弯曲。

7 冗余比值和系统参数

表1总结了不同模型的冗余比值。根据NCHRP的研究,对于初始整体模型超载情况，为考虑充足的冗余度，其冗余比值LFu/LF1应大于1.30。受损的桥应考虑LFd/LF1为0.5以上。

表1 预应力混凝土箱梁的冗余度比值

结构冗余比值是通过对比第一个构件发生破坏时结构的承载能力得到的[16]。如模型1中线弹性pushover分析得到，水平荷载P1=2 272 kN时，系统的第一个构件发生了破坏，即墩柱底端达到了其抗弯承载力。而在非线性pushover分析中，结构的极限承载力为Pu=3 266 kN。模型3的线性pushdown分析中，当两列HS-20卡车荷载施加在跨中时，当荷载增加到LF1=18.0时，正弯矩区第一个构件发生破坏。而在非线性pushover分析中，极限荷载对应的卡车荷载为LFu=24.1。模型1～3的结果表明该桥承受水平或竖向超载时在承载能力极限状态显示出了很好的冗余度。尽管上下部连接采用铰结的模型比刚接的结果低8%，但铰结系统仍能够提供准确的冗余度。后面在纵向荷载的分析研究中表明，整体连接考虑了相似的冗余度。模型4-a、4-b和模型5同样显示了在竖向荷载下大于最小冗余比值0.5的冗余度结果。该多室梁桥满足NCHRP的研究中提供的冗余标准。然而，在同等荷载条件下，单室箱梁显示了非冗余性。

基于pushover和pushdown分析结果，采用可靠度分析来校正系统参数，通过表1的冗余比值结果，表2给出了系统参数对于典型的单箱室和多箱室预应力混凝土箱梁的推荐值。在表2中，风险系数代表在估计荷载效应和承载力时的不确定性；1.1代表了双墩柱结构的系数；0.24为曲率系数；是通过截面分析得到的墩柱的极限曲率；对于薄弱的连接构件考虑了曲率的修正系数（见式3）；为一自由柱的平均曲率，为典型的约束墩柱的平均曲率。一个墩柱屈曲或两个墩柱的结构有一个墩柱破坏的情况按照非冗余性结构考虑。对于非冗余性结构，考虑动力地震灾害和其他水平荷载，系统参数分别取0.75和0.85。

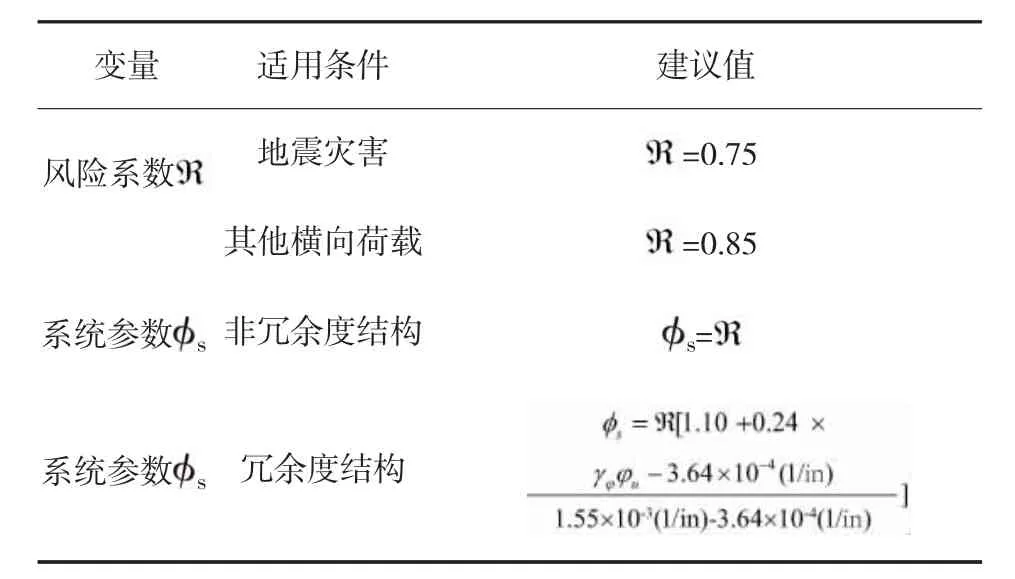
表2 水平荷载下单室和多室箱梁的系统参数

表3列举了在竖向荷载下对于典型单室和多室预应力混凝土梁桥系统参数su和sd的推荐建议值。在表3中，针对AASHTO LRFD桥梁设计规范（式1）的抗力部分，单箱室箱梁的系统参数取0.8是为了让构件比考虑冗余度设计的结构提供更高的安全水平。然而对于多箱室梁桥，初始整体结构的系统参数取s=1.0。对于单根墩柱破坏或腹板破坏的冗余度结构，系统参数s=1.2。

表3 竖向荷载下单箱室和多箱室梁桥的系统

修正系数按如下计算：

式中：M实际为诸如横梁和承台等连接构件的抗弯承载力或实际箍筋、锚固长度、接头或连接构造处的等效弯矩；Mp墩为墩柱的塑性抗弯承载力；Mu墩为采用非线性截面分析的墩柱极限承载力或按照保守估计取1.15倍的Mp墩；φu为最弱墩柱的抗弯极限曲率；φu连接件为所有连接构件的最小极限抗弯曲率。

8 结论

本文主要进行了在竖直和水平荷载下多箱室预应力混凝土箱梁的冗余度研究以及多箱室和单箱梁结构的对比。得到以下结论：

（1）承受竖向荷载的桥梁结构，分析计算表明根据NCHRP的研究提到的，当多箱室结构在设计时满足冗余度要求时，其在整体阶段拥有足够的冗余水平，在单根柱破坏或单根腹板破坏下，能够表现良好的结构冗余度。

（2）对于单箱室梁桥，在腹板承受相同的荷载下，其结构表现为非冗余性。

（3）当结构承受横向荷载时，单根柱屈曲或双墩系统的某根柱破坏的结构，也表现为非冗余性。

（4）本文提出了一系列考虑结构冗余度的预应力箱梁系统参数，提出的系统参数可以用于承受竖向或水平荷载的预应力箱梁结构特别是新型桥梁多箱室箱梁桥的设计和安全性评估。