基于MATLAB的DEM粗差探测算法比较分析

崔学敏

(山东省地质矿产勘查开发局第五地质大队)

数字高程模型(DEM)是地理信息系统(GIS)的重要数据源，已成为国家空间数据基础设施的基础内容之一。对于DEM数据来讲，其精度是最重要的质量评价指标。由原始数据(地面测量、雷达干涉、航空三维激光扫描、航空航天立体摄影测量及利用等高线地形图进行矢量化等)构建的DEM可能会存在粗差，易导致DEM发生扭曲失真。对粗差进行有效探测及剔除，有利于提高DEM数据质量[1-3]。近年来，大量学者对DEM数据粗差探测方法进行了大量研究，大量高精度探测算法相继被提出[4-8]。为进一步探讨目前常用的粗差探测算法的适用性，本研究着重对Felicisimo加权平均算法、Felicisimo十字交叉算法、基于趋势面和三维可视化的粗差探测算法、基于坡度信息的粗差探测算法、基于点方式的粗差探测算法、抗差移动三次曲面拟合算法的技术原理进行分析，并结合MATLAB编程试验，分析各类算法对于不同地形的适用性。

1 粗差探测算法原理

Felicisimo算法按照所取邻域点的不同，分为十字交叉和加权取平均2种算法。十字交叉算法所获取的邻域点为距离中心点最近的4个点，呈十字形分布。加权平均算法所获取的邻域点为中心点附近的8个点。Felicisimo算法以中心点的邻域点的高程平均值进行线性内插后作为中心点的高程估值。设邻域内插窗口尺寸为3×3，某DEM格网点的高程估值为Z(i,j)(i，j为点坐标值)

但在一般情况下，可用该点邻域点的高程加权平均值作为中心点的高程估值

Z(i+1,j-1)]+w′[Z(i-1,j)+Z(i,j+1)+Z(i,j-1)+Z(i+1,j)] ，

(2)

基于趋势面和三维可视化的粗差探测算法的趋势面可以有不同的形式，最常用的为最小二乘趋势面。根据相关统计规律，极限误差取2倍或3倍中误差，即当模型误差大于极限误差时，可认为DEM格网数据含有粗差。该算法是利用局部已有的平高点来拟合出测区的曲面(如最小二乘趋势面)模型，利用间接平差法求解出改正数，改正数反映了平高点与所拟合曲面的离散程度，利用中误差作为阈值探测粗差。

基于坡度信息的粗差探测算法的实质是利用中心点周围邻域点在2个方向的坡度变化来建立一种坡度变化趋势，进一步探测中心点2个方向的坡度变化趋势是否符合坡度总体变化趋势，若2个方向的坡度变化偏差均超过阈值，则可判定DEM格网数据含有粗差。

基于点方式的粗差探测适用于非规则格网数据。对于任意1个中心点P，首先确定1个窗口(设半径为R)来选择格网点的范围；然后计算窗口范围内所有格网点高程的算术平均值(或加权平均值)作为P点的高程估值；最后计算P点的高程值与其估值的差值，若差值大于某个阈值，可认P点含有粗差。该算法的基本原理与Felicisimo算法相似，但区别在于该算法适用于非规则格网，而Felicisimo算法适用于规则格网。

抗差移动三次曲面拟合算法是在基于趋势面和三维可视化算法的基础上，降低平差运算中的粗差点的权值来削弱粗差点对于所拟合的趋势面参数的影响，进而使所拟合的曲面更加符合实际地形。

2 试验分析

本研究试验数据来源于某地区比例尺为1∶10 000、高程精度为0.1m、行列间距均为5m的DEM格网数据(包含了鞍部、丘陵、平原、山地、山包等地形数据)，各类地形分别取25个高程数据点。其中，鞍部地形高程数据见表1。对各类地形的高程数据分别加入0.1，0.08，0.05，0.03，0.01m粗差，利用Matlab语言进行编程，分别采用本研究6种算法(分别记为算法1～6)对各类地形高程粗差进行了探测，结果见图1。

表1 鞍部地形测点高程数据 m

分析图1可知：①Felicisimo十字交叉算法(算法1)、加权平均(算法)算法对于平面或斜面的地形进行高程粗差探测效果较好，但对具有地形特征线的地形(如丘陵、山包等凸起或凹陷地形)，高程粗差探测效果较差；②基于趋势面和三维可视化的粗差探测算法(算法3)对于各类地形高程粗差的探测效果均较好，但该方法仅能适应于单一地形，如果测区包含有2种或2种以上地形，探测可靠性将大大降低；③基于坡度信息的粗差探测算法(算法4)对于平原地形的高程粗差探测效果较好，但对于其余地形高程粗差的探测效果较差；④基于点方式的粗差算法(算法5)适用于平原地区，在其余地区尤其是山地适用性较差；⑤抗差移动三次曲面拟合算法(算法6)适用于鞍部、山地、山包等地形。

3 结 语

对Felicisimo加权平均算法、Felicisimo十字交叉算法、基于趋势面和三维可视化的粗差探测算法、基于坡度信息的粗差探测算法、基于点方式的粗差探测方法、抗差移动三次曲面拟合算法的基本原理进行了分析，并对各类算法的适用地形进行了探讨，对于提高DEM高程点的粗差探测精度有一定的借鉴价值。

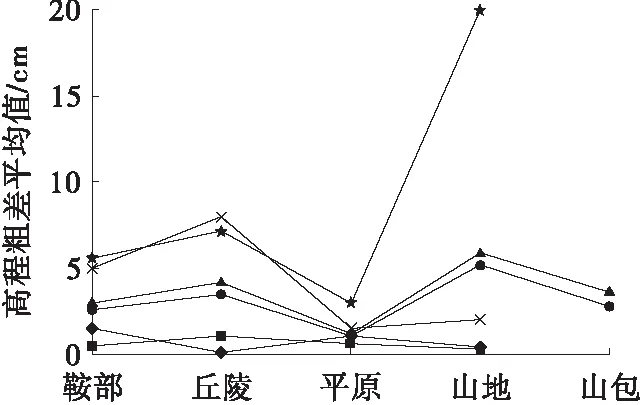
图1 6种算法高程粗差探测结果对比