自驾游背景下考虑参考点依赖的酒店定价策略
郭晓龙,刘兵兵,2
(1.中国科学技术大学 管理学院,安徽 合肥 230026;2.安庆师范大学 数学与计算科学学院,安徽 安庆 246133)
近年来,随着经济水平的不断提升,人们的可支配收入水平也随之增加,国民休闲旅游需求显著提高,私家车保有量也迅速提升。自驾车旅行由于其可以满足年轻旅行者追求个性、自由、体验的目的而受到广大旅行者的追捧,并迅速成为发达地区人们旅游出行的重要方式。
2010年以来,电子商务和移动互联网技术的发展使得消费者接入消费市场的便利性更加显著,在自驾车旅行市场中,消费者仅凭一部手机即可实现“想走就走”的旅行。在旅游目的地的住宿和景区门票等已经不需要在出行前做完整的出行规划。在我们针对三百多名自驾车旅行者的调研中发现:有超过40%的消费者仅收集旅游目的地的相关信息,而其他如住宿、交通等信息均视情况而定,不做提前安排;有10%的消费者表示不制定任何出游计划,甚至不收集旅行目的地的任何信息,真正做“说走就走”的旅行者。
因此,在此背景下,有接近半数的市场需求将在产品所需要时才发生交易,传统的预售(或预订)将不再能够对市场现状做出准确反映。作为旅游产业中的重要组成部分,酒店需要调整其依靠预订建立的销售渠道管理,转而注重针对进入旅游目的地的散客进行销售。研究表明,消费者在购买某种商品时会有一种心理的参考商品(即品类中的代表性品牌),如手机产品中的苹果、三星品牌,运动鞋中的耐克、阿迪达斯品牌,以及网络路由器中的TP-Link等。在酒店行业中也不例外,旅行者到达某个旅游目的地后,在选择酒店下榻时也会有相应的参考行为,典型的参考酒店如黄山风景区中位于光明顶峰顶的光明顶山庄、迪斯尼乐园中的迪斯尼主题酒店等。因此,如何在考虑旅行者参考行为的情况下制定合理的定价策略来实现酒店利润最大化,是景区酒店重要的运营问题。
一、文献综述
基于参考依赖理论与模型的研究可以追溯到20世纪90年代,由2002年诺贝尔经济学奖获得者Tversky和Kahneman于1991年提出并给出了参考依赖模型[1]。此后有大量的学者基于参考依赖模型进行了相关研究,其中与市场策略和定价相关的主要研究有:Bolton等[2]研究发现消费者对过去的产品定价、竞争者产品定价以及产品成本等信息较为敏感,并将基于上述信息形成自己对某种产品的参考价格,进一步在此参考价格的基础上形成自己的购买效用并进行购买决策。He等[3]研究表明:当消费者在网上购物时,被推荐的店铺可以制定一个比未获得推荐的店铺较高的价格。Amaldoss等[4]研究表明:尽管店铺的推荐并不能改变消费者购买某种产品的概率,但可以影响消费者对整个产品种类的价格定位,两位作者进而在Amaldoss等[5]中研究了产品的品牌价值对消费者购买行为的影响。作为参考依赖模型中的重要成分,基于参考行为的购买效用也受到了很多学者的关注,其中KÖszegi等[6]研究发现消费者的支付意愿将受到其对产品的期望价值和预期价格的影响;基于类似的模型,他们在KÖszegi等[7]中发现消费者的风险厌恶特性将导致消费者转移到所有可保风险中。孙娟等[8]从参考依赖的视角针对委托代理模型设计了有效的激励合同;李荣喜[9]在考虑价格参考效应的影响下对消费者需求和产品定价进行了研究。吴鸽等[10]对行为决策理论进行了详尽综述,其他关于参考点依赖理论的研究现状可以参见李荣喜[11]和聂腾飞[12]。
另一方面,酒店作为旅游产业的支柱服务行业,由于其房间数量的确定性、固定成本昂贵而变动成本几可忽略的成本属性,酒店收益管理与定价优化受到了国际同行的高度重视。Lai等[13]针对需求不确定性提出了一种优化模型;Schwartz[14]介绍了一种提高酒店收益的超售策略;Ling等[15]研究了中小型酒店与第三方网站合作时的最优定价策略;Guo等[16]提出了酒店在面临打包产品时的最优定价机制;而Guo等[17]则采用博弈模型研究了酒店与在线旅行商合作时的最优定价机制。Guo等[18]利用市场细分理论,基于酒店的在线预订系统提出了一套动态定价策略来优化酒店收益;Ling等[19]则给出了酒店在开辟在线销售市场时不同状态下的最优定价策略。在在线销售环境中,Dong等[20]研究了酒店与旅行商的最优合作定价决策,而Ling等[21]则基于客房数量分配模型给出了酒店与在线旅行商的最优客房分配方案。考虑到合作方的策略性销售行为,Dong等[22]和Guo等[23]在供应链环境下结合超售策略讨论了酒店的最优定价策略;而Guo等[24-25]则在考虑在线旅行商提供积分返现情形时的酒店定价策略。
尽管酒店的定价优化问题已经得到了相关学者的关注与重视,大多研究均针对垄断市场或在供应链中针对单一酒店的决策优化展开,考虑消费者参考点依赖的研究较少。此外,针对自驾游背景下的酒店管理研究也尚处于起步阶段,现有文献中未发现有针对多家处于竞争情形的酒店展开的定价策略优化研究。因此,本文将在前人研究基础上,利用博弈理论与优化模型,针对处于同一景区的两家竞争性酒店在自驾游背景下考虑消费者参考点依赖行为时的最优定价策略进行研究。
二、问题描述及模型建立
假设一个旅游景点有两家酒店在运营,分别记为H1和H2。假设两家酒店可以全部覆盖该旅游景点的旅行者住宿需求,并且假设在该景点选择入住的旅行者类型x在区间[0,1]上服从均匀分布。旅行者入住酒店获得的固有效用记为V,根据参考点理论,旅行者会以较为出名的酒店作为其参考,并以它为基准来评价其他酒店的质量和定价。为了不失一般性,本文假设酒店H1为旅行者的决策参考酒店(例如黄山风景区位于光明顶峰顶的黄山光明顶山庄)。在他们入住非参考酒店H2时,旅行者除了获得固有的入住效用值V以外,还会去比较酒店H2和H1的价格。具体来说,如果酒店H2的价格p2比酒店H1的价格p1高,则旅行者认为自己的效用有所损失,我们用λ(p2-p1)+表示,其中λ>0表示旅行者对单位价格差产生的效用敏感程度。另外旅行者还会比较两个酒店的质量,基于经典的hoteling模型,酒店的质量可以用到达两个酒店的距离来表示,即如果旅行者到达酒店H1的距离为x(0x1),则达到酒店H2的距离为1-x。对于入住酒店H2的旅行者来说,如果酒店H2的质量(到达距离)1-x比酒店H1的质量(到达距离)x要差(远),则入住酒店H2的旅行者认为自己的效用受损,我们使用μt(1-2x)+来表示此受损效用,其中μ>0表示旅行者关于质量差的敏感程度,t表示单位距离所产生的负效用。根据上述分析,分别可以建立旅行者入住两个酒店的实际所得效用如下:
当旅行者选择入住参考酒店H1时,他获得的实际效用为
U1=V-tx-p1
(1)
当旅行者选择入住非参考酒店H2时,他获得的实际效用为
U2=V-t(1-x)-p2-λ(p2-p1)+-μt(1-2x)+
(2)
三、模型分析
(一)基于完美信息博弈的基本模型分析
首先分析两家酒店对于市场份额的分割情况,可以用当旅行者选择参考酒店H1和选择非参考酒店H2获得的实际效用相等时所占有的份额来刻画。此即旅行者对两个酒店的选择无差异时,这时市场达到了均衡,否则旅行者会选择另外一个能给自己带来实际获得效用更多的酒店。令U1=U2。以下分两种情形讨论。
如果p1≥p2,根据式(2)可知U2=V-t(1-x)-p2-μt(1-2x)+。我们进一步根据两个酒店的质量分为两种情形讨论:即当0x<0.5时,旅行者入住酒店H2获得的实际效用为U2=V-t
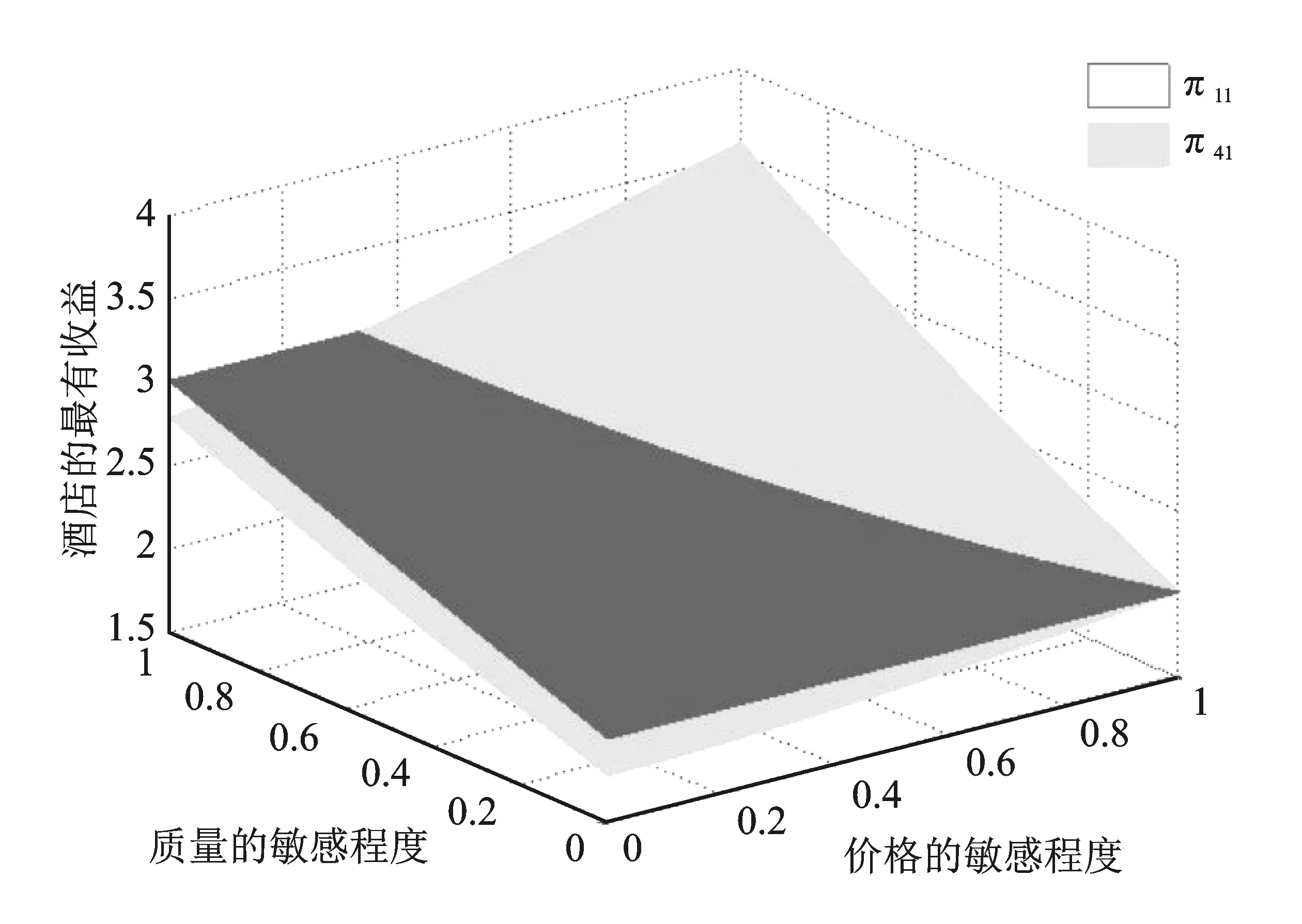
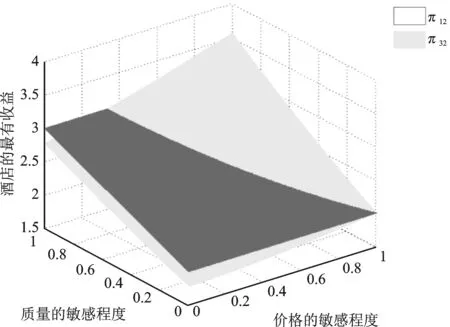
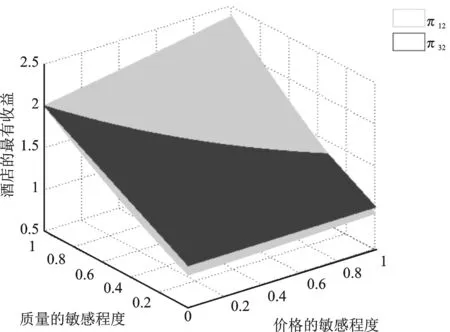
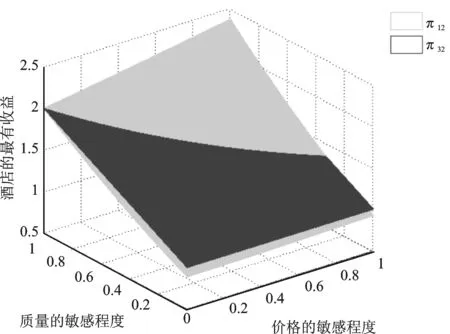
(1-x)-p2-μt(1-2x),令V-tx-p1=V-t(1-x)-p2-μt(1-2x),求解得x1=0.5-(p1-p2)/(2t+2tμ);而当0.5 x1=0.5-(p1-p2)/(2t+2tμ) (3) 如果p2≥p1,此时有U2=V-t(1-x)-p2-λ(p2-p1)-μt(1-2x)+。当0 ≤x<0.5时,旅行者入住酒店H2获得实际效用为U2=V-t(1-x)-p2-λ(p2-p1)-μt(1-2x),令U1=U2,有V-tx-p1=V-t(1-x)-p2-λ(p2-p1)-μt(1-2x),解得x3=0.5-(p1-p2)(1+λ)/(2t+2tμ),由于p2≥p1,显然此时的x3在现实中并不成立。当0.5 x4=0.5-(p1-p2)(1+λ)/(2t) (4) 设π1与π2分别为酒店H1和酒店H2的收益,下面我们根据上面两种情形求解两家酒店在进行定价竞争时各自的最优定价和收益。 1.情形1:完美信息且p1≥p2 当p1≥p2时,根据消费者选择理论,并且知道旅行者市场全覆盖。在信息对称并充分的情形下,非参考酒店H2知道自己会占有较大市场份额,同时参考酒店H1也知道自己会占有较小的市场份额,此时可以分别将π1与π2具体表示为如下的函数形式 π11=p1x1=p1(0.5-(p1-p2)/(2t+2tμ)) (5) π12=p2(1-x1)=p2(0.5+(p1-p2)/(2t+2tμ)) (6) 将两个目标函数分别对各自的价格求一阶偏导数并令其等于零,联立可得 (7) (2t+2tμ))=(t+tμ)/2 (8) (2t+2tμ))=(t+tμ)/2 (9) 综合上述分析,可以得到如下结论: 命题 1 在市场信息充分且对称的条件下,当p1≥p2时,即非参考酒店H2知道自己会占有较大市场份额,同时参考酒店H1也知道自己会占有较小的市场份额时,两个酒店的最优定价相同均为t(1+μ),且两个酒店的收益也相同均为t(1+μ)/2,此时旅行者入住酒店获得的实际效用为V-(1.5+μ)t。 2.情形2:完美信息且p2≥p1 当p2≥p1时,也即当非参考酒店H2知道自己会占有较小市场份额,而参考酒店H1知道自己会占有较大的市场份额时,则有前面分析可知,此时酒店H1的市场份额为x4=0.5-(p1-p2)(1+λ)/2t,酒店H2占有市场份额为1-x4=0.5+(p1-p2)(1+λ)/2t。此时两个酒店的最优收益分别为π21=p1x4=p1(0.5-(p1-p2)(1+λ)/(2t)),π22=p2(1-x4)=p2(0.5+(p1-p2)(1+λ)/(2t))。将上述两个收益函数分别对各自的价格变量求一阶偏导数并令其等于零,联立可得: (10) (2t))=t/(2+2λ) (11) (2t))=t/(2+2λ) (12) 总结上述分析过程,能够得到如下结论: 命题 2 在市场信息充分且对称的条件下,当p2≥p1时,也即非参考酒店H2知道自己会占有较小市场份额,同时参考酒店H1也知道自己会占有较大的市场份额时,两个酒店的最优定价相同均为t/(1+λ),且两个酒店的最优收益也相同均为t/(2+2λ),此时旅行者入住酒店获得的实际效用为V-(3+λ)t/(2+2λ)。 命题1和命题2中的结论表明:在市场信息充分且对称的情况下,无论两家酒店如何估计自己的市场份额,在市场达到均衡时,两家酒店的最优定价和收益一定是相同的。但是,当非参考酒店认为自己的市场份额较大时,两家酒店的最优定价和最优收益均高于非参考酒店认为自己的市场份额较小时的情况。 以上讨论的是在信息对称且非常充分的情形下,两个酒店在进行竞争时所采取的定价策略以及能够达到的最优收益。如果市场信息不充分,此时两个酒店并不能完全了解市场的动向,因此可能导致两家酒店会对自身所占市场份额估计产生偏差或错位。在此情形下,我们应该讨论以下两种情况。 1.情形3:非对称信息且p1≥p2 在p1≥p2条件下,如果非参考酒店H2对市场掌握信息不足,认为二者价格关系为p1≤p2,导致对可能所占市场份额估计不足而认为消费者临界点为x4=0.5-(p1-p2)(1+λ)/(2t),则此时非参考酒店H2的收益函数为π32=p2(1-x4)=p2(0.5+(p1-p2)(1+λ)/(2t)),而参考酒店H1的目标函数仍为π31=p1(0.5-(p1-p2)/(2t+2tμ))。将两个目标函数分别对各自的价格变量求一阶偏导数并令其等于零,联立可得: (13) (t/18)(4/(1+λ)+4(1+μ)+ 1/((1+λ)2(1+μ))) (14) (2t))=(t/18)(4/(1+λ)+4(1+μ)+ (1+λ)(1+μ)2) (15) 命题 3 在市场信息不充分的情形下,当p1≥p2时,如果非参考酒店H2对自己会占有的市场份额估计不足,此时酒店H2的最优定价比参考酒店H1要低,酒店H2的最优定价为2t/(3+3λ)+(t+tμ)/3,而参考酒店H1的最优定价为t/(3+3λ)+(2t+2tμ)/3;但酒店H2的最优收益要比酒店H1的最优收益要高。其中参考酒店H1的最优收益为(t/18)(4/(1+λ)+4(1+μ)+1/((1+μ)(1+λ)2)),非参考酒店H2的最优收益为(t/18)(4/(1+λ)+4(1+μ)+(1+λ)(1+μ)2)。 该命题表明:如果非参考酒店H2认为参考酒店H1的定价不低于自己的定价,对自己的市场份额占有率估计不足时,最终会导致其实际最优定价严格低于参考酒店H1的定价。但由于其相对较低的定价导致非参考酒店H2获得了较多的实际市场份额,进而使得其总收益要严格高于参考酒店H1。 2.情形4:非对称信息且p2≥p1 类似的,在p2≥p1条件下,如果非参考酒店H2由于信息不充分导致错位估计自己可能所占的市场份额较大时,则非参考酒店H2的收益函数为π42=p2(1-x1)=p2(0.5+(p1-p2)/(2t+2tμ)),参考酒店H1的收益函数仍为π41=p1(0.5+(1+λ)(p2-p1)/(2t))。求出它们对各自价格变量的一阶偏导函数令其等于零,并联立可得: (16) (t/18)(4/(1+λ)+4(1+μ)+(1+λ) (1+μ)2) (17) (t/18)(4/(1+λ)+4(1+μ)+1/ (1+λ)2(1+μ)) (18) 命题 4 在市场信息不充分的情形下,当p2≥p1时,即如果非参考酒店H2对自己会占有的市场份额估计较大时,此时酒店H2的最优定价比参考酒店H1要高,非参考酒店H2的最优定价为t/(3+3λ)+(2t+2tμ)/3,而参考酒店H1的最优定价为2t/(3+3λ)+(t+tμ)/3;且非参考酒店H2的最优收益要比参考酒店H1的最优收益要低。具体来说,参考酒店H1的最优收益为(t/18)(4/(1+λ)+4(1+μ)+(1+λ)(1+μ)2),非参考酒店H2的最优收益为(t/18)(4/(1+λ)+4(1+μ)+1/(1+λ)2(1+μ))。 该命题表明,如果非参考酒店H2认为参考酒店H1的定价不低于自己的定价,且对自己的市场份额占有率估计过大时,最终会导致其最优定价严格高于参考酒店H1的定价。由于其相对较高的定价导致非参考酒店H2获得了较少的实际市场份额,进而使得其总收益要严格低于参考酒店H1。 在本小节中我们来分析当两个酒店进行竞争时,所得到的4种情形下的均衡策略是否存在占优策略。如果存在占优策略则说明:不管对手如何行动,每家酒店都有对自己来说最优的竞争策略。表1给出了两家酒店竞争时所采取的策略组合。 由前面分析可知,当0<λ<1且0<μ<1时, 表1 两家酒店的4种策略组合 对于0<λ<1且μ>1以及λ>1且0<μ<1两种情况,理论上的结论分析起来较为复杂,因此在数值实验部分通过数值分析来观察两个酒店的最优收益在4种情形下的大小关系,然后尝试去分析是否存在占优均衡。 下面来分析λ>1且0<μ<1的情形。取λ=(1),(2)且μ=(0),(1),令λ的取值步长为1,令μ的取值步长为0.1。图3和图4分别给出参考酒店H1和非参考酒店H2当λ>1且0<μ<1时分别在情形1与4和情形1与3下的最优收益比较。 图1 酒店H1在情形1和4中的最优收益比较 图2 酒店H2在情形1和3下的最优收益比较 从图3可以发现,当λ>1且0<μ<1时,酒店H1在情形1与4中的收益函数曲面也形成了相交曲线,由前面分析可知,该曲线方程是(1+λ)(1+μ)=4。 图3 酒店H1在情形1和4下的最优收益比较 图4 酒店H2在情形1和3下的最优收益比较 鉴于自驾游的快速发展及其在国民经济中占据着重要的地位,本文针对自驾车旅游市场中的重要服务组成部分——酒店——的竞争定价策略进行了详细研究。模型考虑了消费者的参考点依赖行为特性,针对酒店入住市场全覆盖情形下的两家竞争性酒店,从完美信息与信息非对称两种角度对酒店的最优定价决策进行了分析。研究发现,两家酒店可以在完全市场信息的情况下实现利润最大化,而任何一方的信息缺失将会导致两者利润的受损。因此,本文的管理启示为:处于同一景区的酒店应该结成商业联盟来充分分享其市场信息,使得所有酒店都能知晓其他酒店的市场信息,包括定价,质量和床位数量等,基于这些信息每家酒店都可以制定自己的最优定价决策以实现所有酒店整体利润的最大化。所有酒店不应该把彼此看作为竞争对手,由于每家酒店的消费者定位和酒店风格不尽相同,因此互相直接竞争不仅不会带来更多的收益还会使自己的原有收益受损。相反,酒店更应该注重自己的经营质量、酒店文化和特色建设,以个性化引领市场来吸引消费者而不是通过价格战来达到目的。处在同一景区内的不同层次、不同特色的酒店从消费者角度来看应该是互为补充的角色,彼此互相合作互通有无才能获取市场中的最大利润。除此之外,本文基于理论模型给出了酒店最优的具体定价决策,可以为酒店的运营管理与市场定价策略提供参考。未来研究可以在考虑市场需求随机或非全覆盖市场的情形下展开。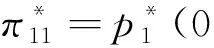
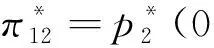
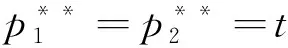
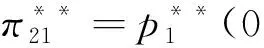
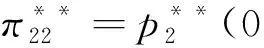
(二)基于非对称信息博弈的模型扩展研究
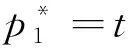
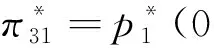
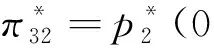
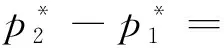
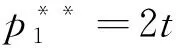
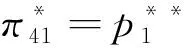
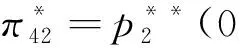
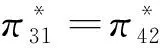

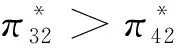
四、占优策略均衡讨论
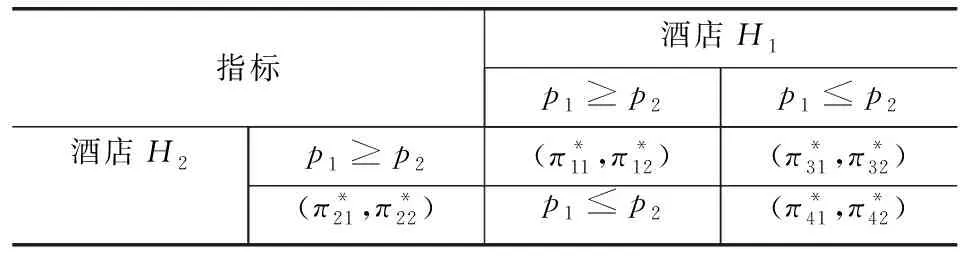

五、数值实验与管理启示

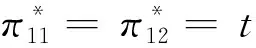


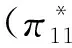
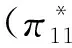
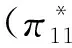
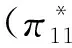
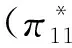
六、结语

