“中国式过马路”行为随机尖点突变模型

林徐勋 ，袁鹏程 ，朱佳翔，张春勤

（1.常州大学 商学院，江苏 常州 213164；2.东南大学 经济管理学院，南京 210096；3.上海理工大学 管理学院，上海 200093；4.浙江理工大学 建筑工程学院，杭州 310018）

近年来，随着城市化建设的快速推进，持续增长的出行需求给城市交通带来了巨大压力，行人与机动车争抢道路资源的现象随处可见，在道路交叉口，行人往往是“凑够一撮人就走，管它红灯或绿灯”，这种现象在中国尤为严重，因此被冠以“中国式过马路”的“美称”。据有关部门统计[1]，2008～2010年，北京市由行人闯红灯引起的交通事故占行人违规致因事故的30%以上；2006～2010年，行人过街引发交通事故死亡率从7.0人/万人增加到10.3人/万人。可见，“中国式过马路”现象不仅严重威胁行人出行安全，并导致通行能力下降、车辆滞留，加剧交通拥堵，造成极大社会损失和不良影响；而由此引发的道路交通安全问题也已成为社会关注的热点。目前，国内各地对这种现象尚缺乏有效的手段，导致“中国式过马路”现象常态化。因此，如何更有效地预测和治理“中国式过马路”行为已成为困扰城市交通管理的难题。

现象上分析，“中国式过马路”主要有如下特征：①群体行为。当过街人群积累到一定数量时，便以整体队列的形式强行横穿马路。②从众效应。当一部分人开始率先强行闯红灯时，周边等待行人会产生从众心理，导致许多最初没有闯灯意识的人也参与到“闯红灯”的队列中。③“突变”现象。行人过街行为的产生并不是以一种连续、渐进的方式进行，而是到一定时刻点之后呈现群体“爆发式”特点，具有不稳定性和难预测性，给过往驾驶员造成极大的心理压力。

目前，虽然对“中国式过马路”现象已经有过很多的报导，但现有出行行为分析主要集中于通勤行为预测[2-3]、活动-出行选择[4-6]以及路径选择与拥挤收费[7-9]等方面的研究，对“中国式过马路”行为的理论研究并不多见。少量相关研究主要运用经济学、心理学及行为分析等方法对过街行为预测、法治与安全意识、出行心理以及过街交通流建模等内容进行探讨，主要包括：

（1）网络设计与交通流建模。Yu等[10]建立了过街行人离散分布条件下过街网络设计优化模型；Jin等[11]运用交通流模型分析了行人过街行为对道路通行能力和车辆行程延误所造成的影响；Yang等[12]通过仿真模拟再现了行人过街较高的闯灯概率；Chen等[13]运用元胞自动机模型（CA）模拟了需求随机和不同初始过街位置下的过街行为。

（2）过街行为建模及影响因素分析。Li等[14]拟合了行人过街等待时间概率分布，显示不同个体等待时间的显著差异；Sun等[15]研究过街行人在不同条件下对车辆速度和刹车距离的估算；Li等[16]刻画了过街风险对行人等待时间的影响；Koh等[17]拟合了行人过街可接受车辆间距随机分布；Sueur等[18]从风险承受角度探讨不同人群过街行为的异同点；Rosenbloom 等[19]验证了群体行为对个体决策的显著作用；Brosseau等[20]通过蒙特利尔市的实测数据分析主客观因素对过街行为的影响，研究结果表明，等待时间超过一定阈值时，大部分行人开始强行过街，表现出过街行为决策的“突变”现象。

（3）过街行人心理分析。Zhou等[21-22]运用计划行为理论验证过街行人的“从众”心理；Rosenbloom 等[23]研究儿童过街行为，得到与文献[21-22]中类似的结论；Harvard等[24]探讨人行横道的设置对行人过街安全心理的正面作用；Liu等[25]及Lipovac等[26]分析行人过街闯灯行为过程中的风险承受心理；Faria等[27]通过实际观测数据分析过街行为的群体性影响，并阐述了过街行人面对密集车流量时“进退两难”的心理状态。

现有研究从多方面对行人过街现象进行了一定的分析，但多数研究主要依赖定性分析与数据挖掘，缺少对“中国式过马路”行为决策内在机理的深层剖析；其次，现有研究主要从“连续变化”的视角分析行人过街决策的改变，缺少对实际过街行为中“突变”现象的理论探讨；另外，现有研究主要着眼于静态均衡视角下的过街行为，较少考虑“中国式过马路”行为的动态演化以及演化过程中随机扰动的作用规律。因此，存在进一步深入的空间。

近年来，演化博弈被越来越多地运用到各类行为决策研究中，涉及环境污染治理[28]、技术合作创新[29]和企业制度提升[30-34]等众多领域。演化博弈考虑不完全信息条件下博弈参与方有限理性的特点，以动态均衡视角解析博弈参与方相互作用关系，不仅能够得到博弈的最终结果，还能计算博弈过程的演化轨迹，全面反映博弈决策行为的实时变化特征。本文运用演化博弈思想解析“中国式过马路”行为决策过程；在其基础上加入高斯白噪声随机扰动过程，分析随机扰动作用下模型的突变类型和解析性质；进一步，运用随机尖点突变理论探讨过街行为中策略选择的突变现象；最后，通过算例探讨随机扰动对过街行为的影响作用，寻找突变临界面与相关因素的关系。研究结果为行人过街策略的预测和违章过街行为的治理提供了新的思路。

1 “中国式过马路”博弈决策行为分析

以“中国式过马路”现象中具有闯灯倾向的行人为研究对象，通常可以观察到两个阶段：首先有为数不多的一群先行者开始强行过街；随后一大部分人群开始跟随加入过街队伍，逐渐形成强大的闯红灯群体，拉开“中国式过马路”的序幕。根据上述现象归纳出本文所建博弈模型的3个假设条件：

（1）效用。过街行人效用与闯红灯而缩短的通行时间成正比，与交警惩治力度成反比。

（2）决策。行人具有两种选择策略：①选择先行带队闯红灯（简称“先行”）；②观察到他人的先行闯灯行为后跟随加入（简称“跟随”）。

（3）惩治。交警负责惩治，但是由于警力有限，交警以一定概率对先行闯红灯者进行惩治处罚。

综上所述，得到“中国式过马路”的单期博弈收益矩阵，如表1所示。

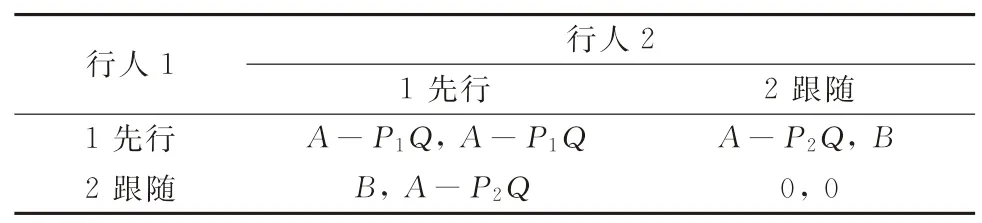
表1 单期博弈收益矩阵

其中：A为先行闯红灯者的收益；B为经过一段时间后跟随闯红灯者的收益；Q为交警处罚造成的行人效用损失；P1为博弈双方均选择先行闯红灯（策略①）而受到交警惩治的概率；P2为博弈双方选择不同策略闯红灯时先行者受到交警惩治的概率。

根据上文所给的3个假设条件不难得到上述参数的关系，即A＞B＞0，Q＞0，P2＞P1＞0。

设x（t）表示在时刻t选择先行闯红灯（策略①）的行人比例，则0≤x（t）≤1；根据演化博弈的思想[34]，每个行人在博弈中选择先行策略（策略①）以及跟随策略（策略②）的期望收益分别为：

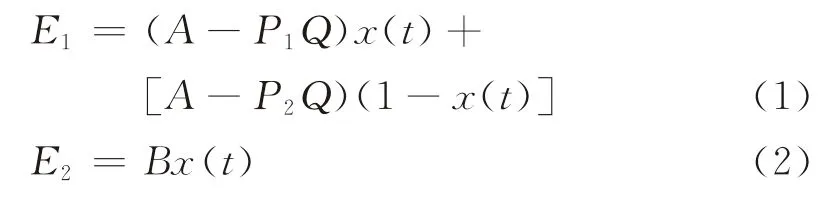
根据式（1）、（2），可得群体收益为

由此得到动态演化博弈方程：

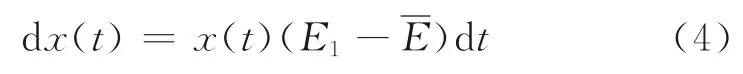
化简得如下关系：

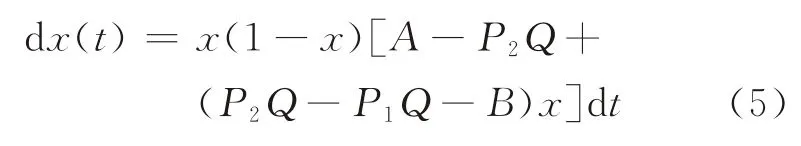
2 “中国式过马路”行为随机尖点突变模型

演化博弈方程式（1）～（5）体现了行人在不同环境下行为决策的动态演化过程，以“确定性系统”的视角来分析行人过街决策，但决策过程通常受到各类随机因素的干扰，包括行人本身的心理、性格、情绪，以及过往出行经验；还包括外部环境的不确定性，例如天气、交通事故、自然环境等。这些随机因素难以被捕捉和量化，但会改变最终的决策结果。因此，不能被轻易忽略。为了反映这种不确定性干扰，参照相关研究的做法[35-38]，本文在式（5）的基础上引入高斯白噪声扰动，得到如下关系：

式中：w（t）表示布朗运动；dw（t）表示通常意义上的高斯白噪声；δ（x）为扩散系数，反映t时刻的扰动强度。

这样，x（t）便从原来的固定变量转变为随机变量，通过多种可能的演化轨迹集合显示行人决策行为的随机性；记x（t）的概率密度函数为

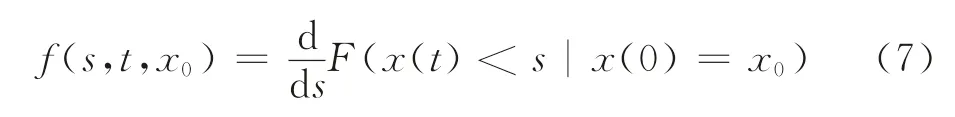
式中：t为时间变量；s为自变量；x0为演化起始点；F（s，t）为x（t）的累积概率函数。令

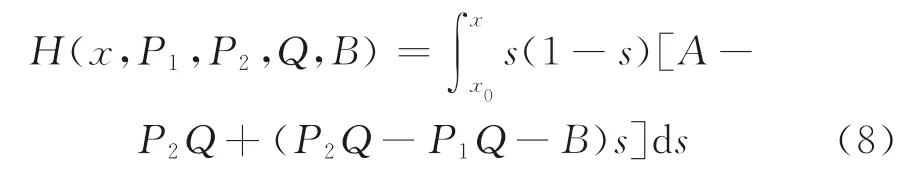
则式（6）可写为如下随机突变模型表达式：

式中，H（x，r）为系统势函数，反映x（t）与模型控制变量的映射关系。其中：x（t）为系统状态向量；r=（P1，P2，Q，B）为系统控制向量；dw（t）与δ（x）含义同式（5）。

进一步，根据Cobb等[37]关于随机过程意义上的“随机均衡”研究，当t→+∞时，式（6）所示f（s，t，x0）一致收敛，其极限函数满足如下关系：

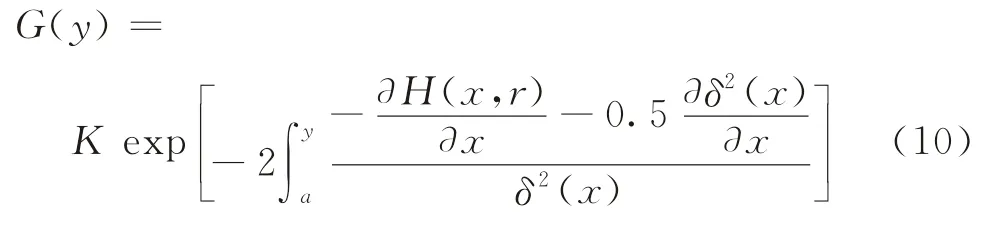
式中，K为标准化常数，保证G（y）在状态空间中的积分为1。简单起见，令δ（x）为常数，记为δ，则式（10）可进一步化简为

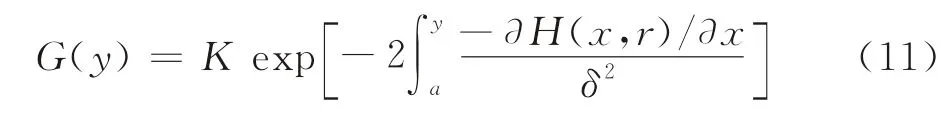
对于交通管理部门而言，对过街行为决策过程的了解是制定相关管理政策的前提和基础，本文运用随机尖点突变理论刻画行为决策中的“突变”现象，分析随机扰动对均衡结果的影响，对比不同状态下出行者对相关政策的敏感度。为随机条件下行人过街管理提供决策依据。首先，根据上文的理论分析，可以得到如下结论：

定理1当式（6）所示“中国式过马路”随机演化动力学方程满足条件P2Q-P1Q-B≠0时，其极限函数符合“尖点突变”特征。

证明根据式（11）可知，

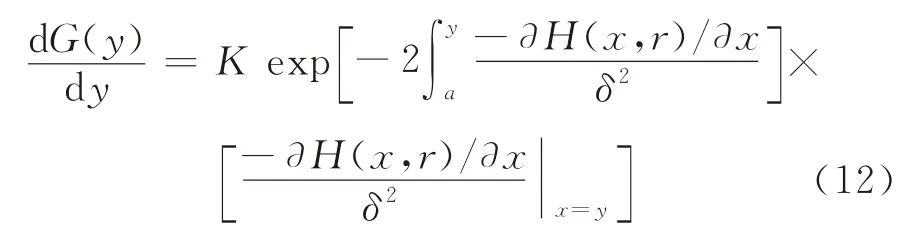
不难推知，

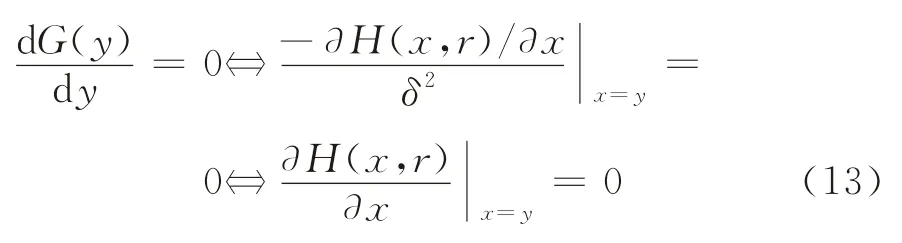
将式（8）代入式（13），可得

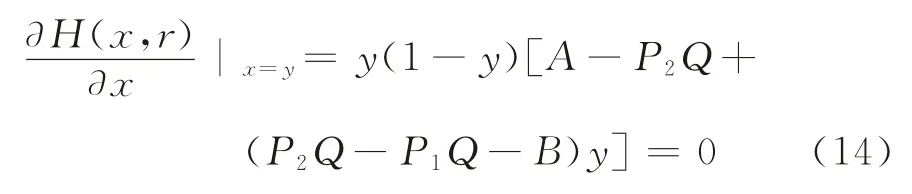
再对y作平移变换，因为P2Q-P1Q-B≠0，令

式中：u、v为系统控制变量；z为系统的状态变量；根据尖点突变的形式[35-38]可知，式（18）所示演化收敛函数符合标准的尖点突变模型。 证毕

根据定理1的论述可知，考虑了随机效用的影响后，当行人过街决策行为演化过程满足一定条件时，行人最终的博弈结果会发生“突变”，即先行闯灯比例从某个稳定状态突然变化至另一稳定状态的显著非连续变化。进一步，讨论突变发生时刻的控制参数临界集合，即突变发生时，控制参数所满足的条件，得到如下结论：

定理2“中国式过马路”演化博弈过程中，当满足如下两个条件时，过街决策行为将发生“突变”现象：①式（6）所示“中国式过马路”随机演化动力学方程满足P2Q-P1Q-B≠0；②控制参数满足A-P2Q=0或A-P1Q-B=0

证明根据条件①可知，式（15）成立，根据突变理论可知，突变状态发生的临界面即式（18）所示曲面在（u，v）方向的投影，根据空间解析几何原理可知，式（18）所示突变发生时的临界面满足如下两个条件：

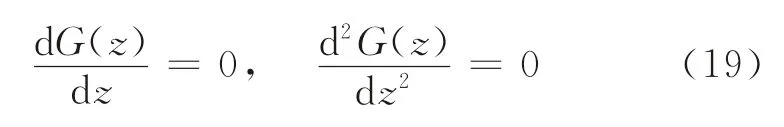
将式（11）代入式（19），得：

式中，u、v含义同式（17）。将式（20）化简得

将式（17）代入式（21），化简得

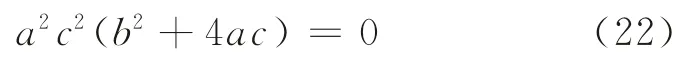
因为a≠0且b=a-c，所以式（21）等价于c=0或a+c=0。根据式（16）中a、b、c含义可知，“突变”发生的临界面的表达式为：

因此，当演化过程中参数连续变化并在该曲面某点临域内穿过曲面时，过街行人行为决策发生巨大变化，行人开始群体性强行过街，引发“突变”现象的产生。

3 “中国式过马路”行为决策随机均衡与突变现象分析

根据定理1可知，式（6）所示行人过街随机演化系统满足尖点突变的形式，为了更直观地体现考虑随机效用影响下，“中国式过马路”过街行人的动态突变行为并探讨合理的管治措施，本文针对所建随机演化博弈模型进行数值仿真，考虑如下几方面的影响作用。

3.1 红灯时间对系统随机演化的扰动作用分析

令B=15，Q=90，P1=0.375，P2=0.75，δ（x）=0.3；设红灯时间A从40逐渐增加到90，得到随机演化过程如图1所示。图1（a）、（b）分别为确定条件与随机扰动的演化过程（图1（a）介于0和1）。从演化路径来看，确定条件下的演化路径趋势明显，呈单调变化趋势；而随机扰动条件下演化路径呈明显上下波动趋势；特别注意A=60时，确定条件下的演化曲线迅速趋向于0（图1（b）），而受到随机扰动后迅速趋近1，并一直以1为期望值作小区域平稳波动（图1（a））。可见，随机扰动能够改变过街行为演化的最终结果。

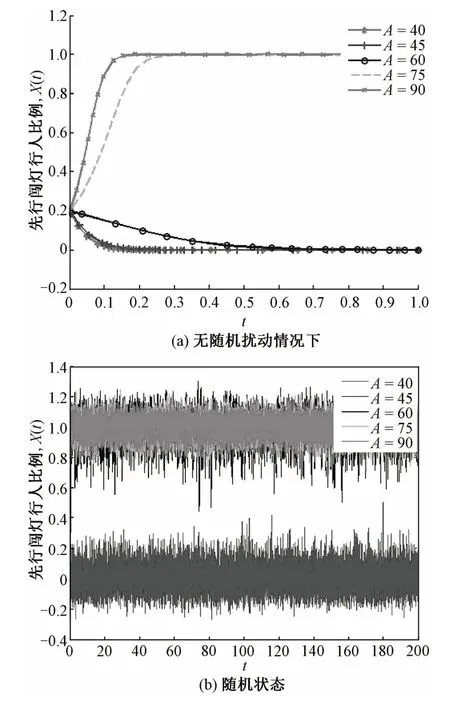
图1 红灯时间变化下的行人过街状态演化示意图

其次，观察红灯时间变化影响下行人过街行为的“突变”现象，如图1（a）随机演化曲线所示。当红灯时间A从40变化至60时，先行闯灯行人比例一直在0附近波动；而A取值大于60时，演化轨迹从原来0 的邻域突然跃迁到1，中间没有任何过渡。把这种过街行为表现出的“跳跃性”变化称为“结构性突变”，而这种突变是由于博弈过程的内在机理受到随机扰动而引起的，是随机演化的最终结果。说明在实际交通环境下，行人博弈存在“临界边界”，一旦越过这个边界，行为选择就会发生显著变化，表现出“突变”现象。

进一步，从理论上分析“突变”现象的内在机理。根据定理1计算得图2（a）所示系统三维演化图，图2（b）表示突变曲面在控制变量u-v平面的投影边界，点1～5依次对应红灯时间A在不同取值下的控制变量二维值；根据定理2计算得到点1、2位于突变边界线上，点3～5位于突变平面内部。可见，当参数A发生变化时，控制变量v从突变边界转移到平面内部，状态变量z从三维曲面的上叶沿着边界突变到下叶，行人过街行为突变现象随之发生。

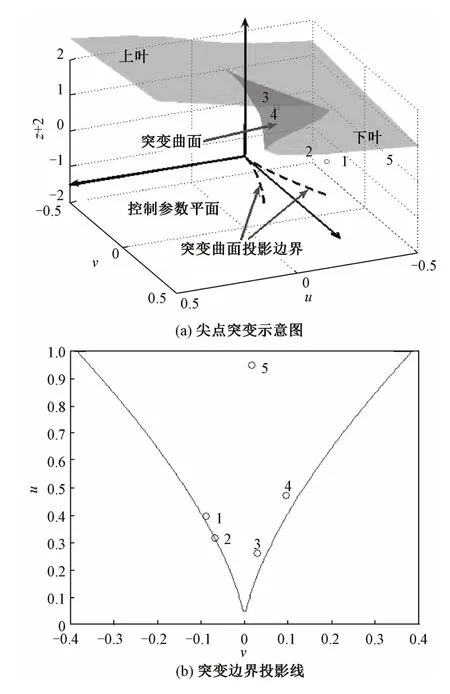
图2 红灯时间动态变化下的过街行为突变示意图

最后，根据式（11）计算得到图3所示红灯时间动态变化下行人先行闯灯比例极限概率密度函数。可见，在红灯时间逐渐增大的过程中，极限概率密度函数也发生了明显的“突变”现象。当A=40时，极限概率密度函数呈明显的“左尾”，表明行人以较高概率选择遵守交通规则；而当A=90时，极限概率密度函数出现了明显的“右尾”，表明行人以较高概率选择先行闯灯。因此，图2～3所示系统演化过程均与图1（b）所示系统状态动态演化图所表现出的突变现象吻合，验证了突变现象的正确性。

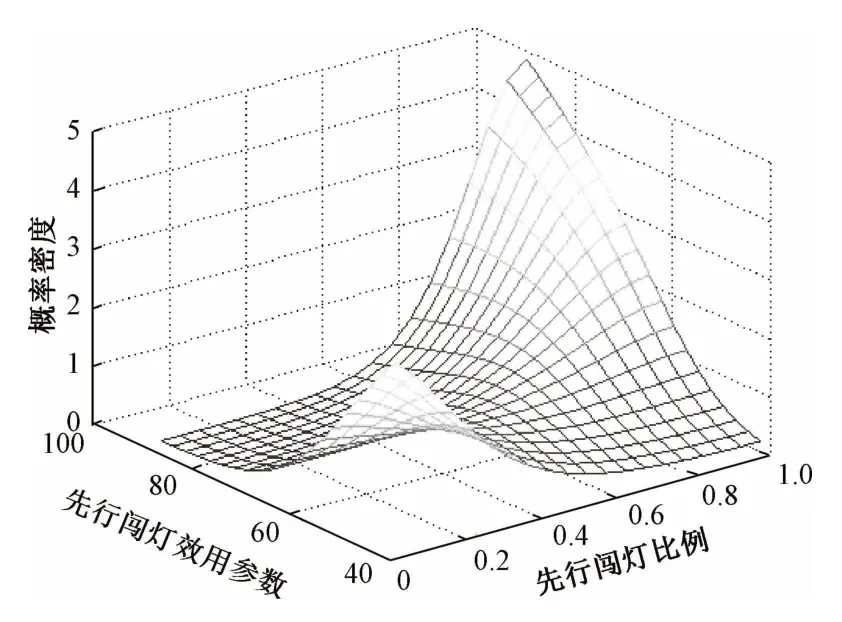
图3 红灯时间动态变化下的极限概率密度函数图

根据上述分析可得如下结论：随机效用的影响能够对行人过街行为产生显著扰动作用；行人更倾向于选择先行闯灯；另外，红灯时间超过一定阶段时，行为发生突变，所有行人以较高比例选择先行闯灯，说明行人等待时间存在“上限”。当超过该上限时，过街行人行为发生明显“突变”，开始选择先行闯灯，这也与实际道路系统中观察到的情形一致[20]。

3.2 跟随闯灯收益变化对系统随机演化的扰动作用分析

令A=60，δ（x）=0.2，B从30变化至55；过街行为随机演化过程如图4所示。图4所示为考虑随机扰动前后行人过街演化状态对比图，虽然演化的路径存在较大差异，但演化的最终稳定点并无显著变化；并未表现出明显的“突变”现象，说明过街行人对跟随闯灯收益参数变化并不敏感。

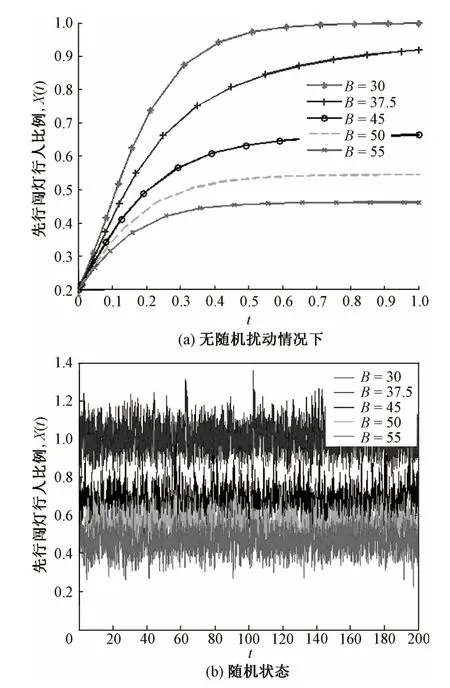
图4 跟随者收益变化下的行人过街状态演化示意图

根据定理2可知，B=37.5时达到突变的临界状态（如点2所示），但并未表现出明显的突变现象。图5（b）所示的极限概率密度函数变化平稳，可以推断，当B发生变化时，点1、2并不处于三维演化曲面的上下叶，而是位于之间的突变曲面上。因此，变化平稳，未出现明显的“突变”现象，也说明本例中过街行人对跟随闯灯收益的敏感性不高。

3.3 惩治措施对系统随机演化的扰动作用分析

惩治措施是当前交管部门采取应对“中国式过马路”现象的常见手段，令B=15，A=60；令惩治措施负效用Q从85逐渐增加到150，得到随机演化过程如图6所示。首先考虑效用随机扰动对演化过程和结果的影响，图6表示未考虑/考虑随机因素影响下的行人过街状态演化示意图。当Q=85，90时，图6（a）显示，在所有情况下过街行人先行闯灯比例最终收敛至0；而图6（b）显示，布朗差随机效用影响下，行人选择先行闯灯。可见，随机效用能够在一定条件下对行人过街选择行为产生显著影响；也表示在惩治措施参数变化过程中行人选择行为发生了“突变现象”。进一步对上述突变行为进行理论分析，图7展示了惩治措施变化下的先行闯灯行为突变内在机理。与上文的分析类似，将式（18）中突变曲面投影到u-v控制平面上，计算突变边界投影线，如图7（a）所示。根据定理2可知，Q=85～90时，系统靠近突变边界线（如点1、2所示），此时，行人过街行为发生突变。最后，考察极限概率密度轨迹，与图3类似，图8所示极限概率密度函数图对不同参数取值的变化过程也表现出了从“右尾”到“左尾”的变化，也验证了突变现象与模型机理的正确性。

图5 跟随者收益变化下的极限概率密度函数图

根据上述分析可得如下结论：在考虑随机效用影响下，出行者对惩治措施的敏感性变弱，应增加惩治力度才能对“中国式过马路”行为产生约束；另外，惩治措施只要跨越过街行为博弈突变的“临界面”，便可收到良好的效果。

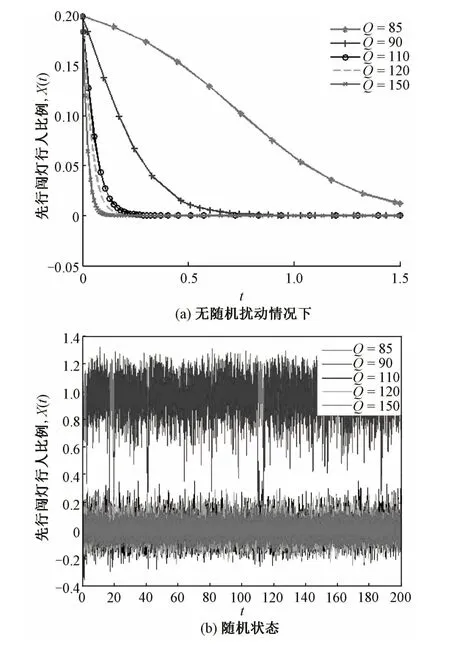
图6 惩治措施变化下的行人过街状态演化示意图

图7 惩治措施变化下过街行为突变示意图

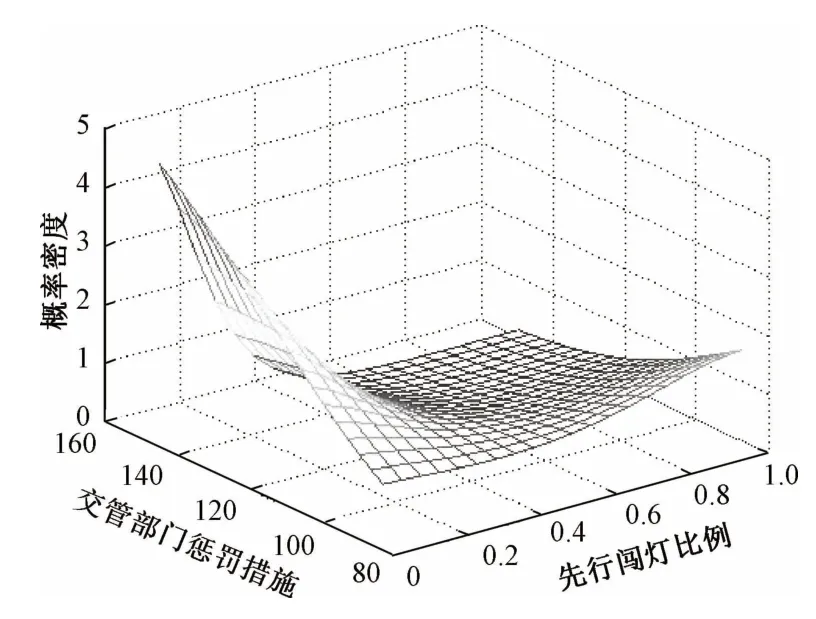
图8 惩治措施动态变化下的极限概率密度函数图

4 结语

本文将“中国式过马路”现象中过街行为分为先行闯红灯和跟随闯红灯两类策略；运用博弈思想建立了行人过街动态演化模型，在此基础上引入布朗运动差刻画随机扰动对过街博弈行为的影响；借助随机尖点突变理论探讨动态过街行为中策略选择的突变性问题，进一步从理论层面论述了过街行为突变现象产生的原因、临界条件和突变过程。最后，通过数值仿真探讨随机扰动对过街行为的影响作用，刻画随机扰动下系统动态演化轨迹曲线特性，给出了相应交通管理策略。研究结果表明：①博弈过程中随机扰动在一定条件下对过街行为的演化模式、过程和最终结果均存在显著影响。②过街行人红灯等待时间存在一定“上限”，在随机扰动影响下，出行者对该“上限”的敏感性提高，行为易发生“突变”。因此，在设置行人过街时间时应考虑尽量不超过该“上限”值。③在随机扰动影响下，出行者对惩治措施的敏感性变弱。因此，应增加惩治力度才能对“中国式过马路”行为产生约束。另外，惩治措施不需要制定的过高，只要跨越过街行为的“突变边界”，便可有效制止“中国式过马路”不良行为。