基于时变时滞模糊双曲神经网络的配电网故障定位方法的研究

邱力伟,关焕新，刘明威

(1.沈阳工程学院，辽宁 沈阳 110136；2.国网沈阳供电公司，辽宁 沈阳 110003)

不断深入的电网建设加速了电网大规模区域性互联的发展趋势，但也促使电网连锁性故障[1]发生的概率增大，对电力系统造成严重威胁。连锁性故障大多由较小的故障引发，如某一继电保护装置的拒动或误动、某段线路短路等，而电网的大规模互联使微小的故障不断传播并加剧，最终导致电网的连锁性故障，发生大规模停电事故。据统计，超过85%的连锁性故障是由于未能及时确定配电网故障区域造成的[2]，因此，提高配电网的故障定位技术显得尤为重要。配电网故障从发生到传播扩大的时间极为短暂，小型故障几秒内就可能发展为连锁性故障，并且故障具有时变性特征，使配电网快速故障定位的难度剧增。

人工神经网络(Artificial Neural Networks,ANN)因其自组织、自适应和自学习的特点被广泛应用于各个领域，在配电网故障诊断的应用中也发挥着越来越大的作用，大量专家学者对此进行了相关研究。2005年毕天姝[3]等提出将正交最小二乘算法扩展用于优化径向基函数神经网络参数，并将得到的新型径向基函数神经网络成功应用于配电网故障诊断问题。但是，该方法的诊断速度一般，并未考虑故障特征的时变性；2008年刘超[4]等人提出运用量子神经网络进行配电网故障定位的算法，借鉴量子力学的相关概念，不断更新各层神经元的连接权以及隐含层各神经元的量子间隔，达到提高故障定位容错性的目的。但是训练速度过慢，也未考虑故障特征的时变性；2017年邱路[4]等人将小波奇异熵与自组织特征映射神经网络相结合，提出一种能够适应微电网系统拓扑结构变化情况的故障诊断方法。该方法虽然不受故障位置、故障时刻等因素的影响，但是仍然没有考虑故障特征的时变性。

上述文献采用的配电网故障诊断方法均能有效诊断配电网故障，但均未考虑配电网的故障的时变特性。本文建立时变时滞模糊双曲神经网络[6](Time-varying Delay Fuzzy Hyperbolic Neural Network,TDFHNN)的模型，并首次将其应用于配电网故障诊断，与上述方法相比，能够快速有效地诊断配电网故障，并且考虑到了配电网故障特征的时变性以及时滞特性。

1 时变时滞模糊双曲神经网络

1.1 TDFHNN的拓扑结构

图1 TDFHNN拓扑结构

在图1所示的时变时滞模糊双曲神经网络拓扑结构中，定义f1(x)=tanh(x),f2(x)=x；定义Kx=diag(k1,k2,…,kn)为模糊隶属函数[7]Pxj与Nxj的中心；aij与bij(i,j=1,2,…,n)表示从输出层的第i个节点到隐层的第j个节点的常量连接权和常量时滞连接权；d1,d2,…,dn>0为常量；τjlj(t)>0(i,j=1,2,…,n,lj=0,1,…,ωj)组成的τ(t)表示时变传输时滞；I1,I1,…，In表示阈值。

1.2 TDFHNN的实现

TDFHNN是一种前馈的三层网络，因此可以通过前馈学习方法对其连接权进行训练，本文选择BP算法[4]，但是其实现过程与传统的BP算法有所区别，具体训练步骤如下。

a. 初始化权值。类似于文献[8]一类的经典BP神经网络可以随机赋予权值初值，但是TDF-HNN本质上是模糊模型，其初值不可以随机选取，必须由专家系统选择初值。

b. 确定结构参数以及定义变量。确定训练样本个数，本文拟定训练样本个数为n；输入变量xi(t)(i=1,2,…,n)，神经网络第n次迭代后输出变量为yi(t)(i=1,2,…，n)；设定期望输出为ξi(t)(i=1,2,…，n)；设定误差精度e。

c. 输入训练样本，样本构建见1.3。

d. 正向传播。将构建的训练样本输入xi(t)(i=1,2,…,n)带入模型，计算出网络的输出yi(t)(i=1,2,…,n)，并求得与期望值ξi(t)(i=1,2,…,n)的误差E(n)。

(1)

式(1)为误差计算公式，训练过程中期望值与输出值的误差E(n)处理方法如下：

如果E(n)>e，则转至环节e;

如果E(n)≤e，则转至环节f。

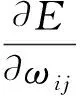
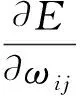
(2)

ωij(n+1)=ωij(n)+Δωij(n)

(3)

式中：ωij(n)表示网络的连接权符号，ωij(n)是多个权值的集合而不是单一的权值；ηi(n)表示网络的学习效率，其选取方法如下：

ηi(n+1)=ληi(n)

(4)

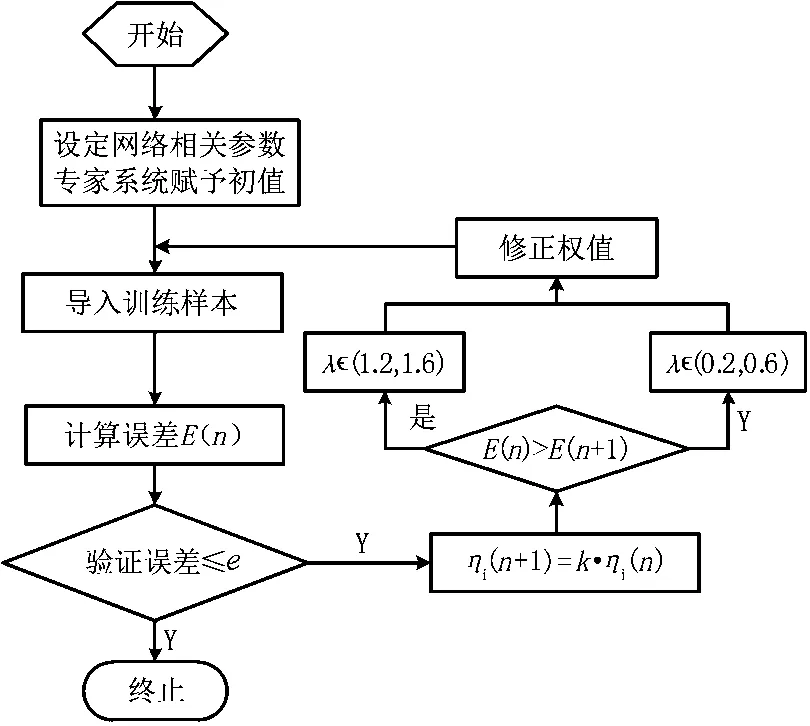
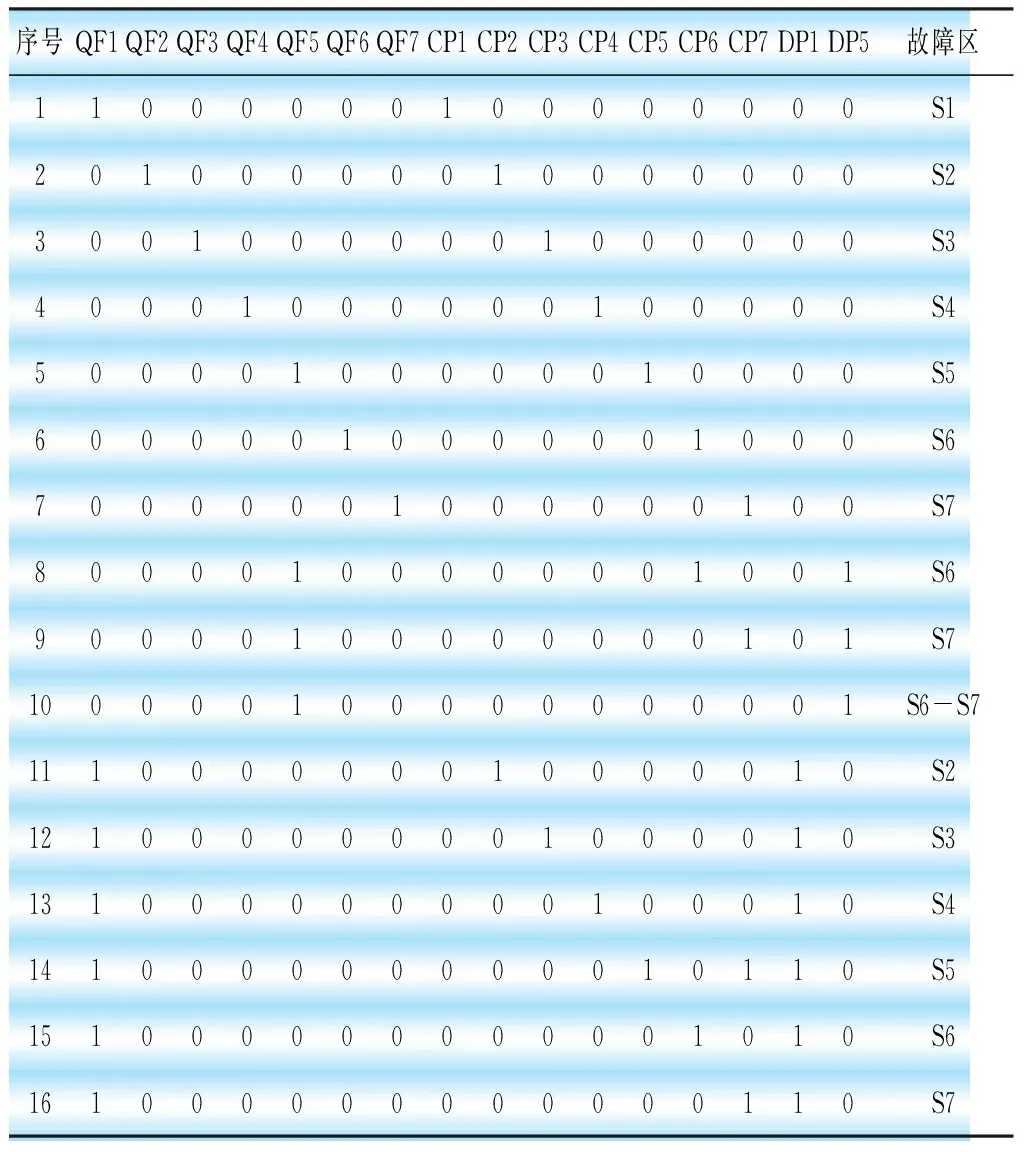
式中：λ的取值遵循以下规则：E(n)>E(n+1)时，λ∈(1.2，1.6)；E(n)

新的参数计算完成后带入环节c继续循环，直至达到指定误差精度e。

f. 算法终止。为了更加形象地说明该算法的具体步骤，本文建立了算法流程图如图2所示。

2 仿真分析

2.1 配电网故障模型

首先构造一简单的配电网络如图3所示，该网络分为7个区域(S1-S7)。均配有过电流保护(CP1-CP7)，S1和S5配有距离保护(DP1、DP5)。

图2 算法流程

图3 配电网拓扑模型

根据图3构造故障决策表(即训练样本)见表1，表1中数字“1”代表断路器动作或保护动作，“0”表示断路器未跳开或保护未动作。

2.2 训练结果

电网模型对应的故障决策表见表1，共16组训练样本。表中有 QF1-CP5 共16个条件属性，因此定义输入变量为16个，神经网络层数为3；输出神经元个数为8，对应8个故障诊断结果；隐含层神经元个数取32。对TDFHNN进行训练，训练结果见表2。

表1 配电网故障决策表

表2 训练结果

2.3 性能分析

为了验证TDFHNN性能的确优于传统的BP神经网络，本文构造了含有保护装置误动信息的9个故障样本如表3所示，对照表3可知，样本1和9是断路器误动，样本2是过流保护装置误动，样本3-8是断路器拒动。然后，分别使用本文构造的TDFHNN以及文献[9]构造的BP神经网络对表3所示的故障样本进行故障定位。表4为2种神经网络对样本的诊断结果，图4为误差的变化曲线。

表3 故障样本信息表

表4 TDFHNN与BP神经网络的诊断结果

由表4诊断结果可以看出，对存在一定错误信息样本的诊断结果，TDFHNN明显优于BP神经网络。主要表现在TDFHNN对各个样本都可以较好地识别，而传统BP神经网络仅能识别出样本2的故障。

图4 误差的变化曲线

由图 4 可知，60个学习步长时，TDFHNN误差已经趋于0，而传统BP神经网络的误差值仍然很大，且比之BP神经网络，TDFHNN误差的收敛速度也很快。

3 结束语

本文构造时变时滞模糊双曲神经网络的拓扑结构，并论述了其实现方法。首次将其应用于配电网故障定位，用仿真分析证明了该方法的容错性与优越性。仿真结果证明了本方法可以适用于配电网容错性故障定位，为今后配电网故障定位的研究提供了一定的借鉴。