温度-车辆耦合荷载对沥青路面设计参数的影响分析*

方明雨 谢逸超 付 军 雷 力

(1.湖北长江三江港区域投资开发有限公司 武汉 436035; 2.宜昌市夷陵区公路管理局 宜昌 443100; 3.武汉理工大学交通学院 武汉 430063)

经验法和力学-经验法是国外的2大类沥青路面设计方法，而目前国外沥青路面设计方法趋向于采用力学-经验法，针对沥青路面的永久变形和开裂2种损坏类型，大都选用沥青层底面拉应变、基层底面拉应变(半刚性基层时)、低温收缩应力、路基顶面竖向压应变、沥青面层永久变形等作为设计指标，很少或者几乎没有采用路表弯沉作为主要的设计指标[1]。而我国由于路表弯沉值便于测量，故沥青路面设计规范以路表弯沉值作为主要设计指标，以沥青面层和半刚性基层底面的弯拉应力作为设计的验算指标，并制定了相应的设计标准。沥青路面基层结构的刚度较大，故难以用反映整体刚度要求的路表面弯沉指标来控制路基的变形或承载力。沥青路面基层和面层的应力状况和大小，主要随上下层的刚度比和层间接触条件而变，他们受路表弯沉大小的影响很小，因而，将路表弯沉作为主要设计指标无法控制沥青路面的基层和面层的应力状况和大小。

关于沥青路面温度场的分析，国内外进行了大量的研究工作，主要分为统计分析法和理论分析法2大种，并且都取得了显著的研究成果[2]。但总体来说，这些研究内容集中在路面温度的分布状况和分布规律上，并未同沥青路面的温度应力联系起来，对于如何将其应用于实践，也涉及较少，原因在于实测沥青路面的温度应力非常困难。目前对温度应力的研究大多通过室内试验的方法进行[3-5],因此，建立合适的数字模型，进而将理论计算与试验分析相结合以研究沥青路面温度应力具有重要意义。对沥青路面结构的设计指标，国内外虽然有一些研究和探索，但存在未考虑温度荷载等问题。本文建立沥青路面的三维有限元模型，分析了温度-车辆耦合作用下沥青路面的力学响应，并探讨沥青路面的设计指标。

1 沥青路面设计参数指标

沥青路面的性能居于柔性路面与半刚性路面之间，由于柔性路面整体刚度较小，导致路面变形较大，故沥青路面应控制路表弯沉值作为衡量路面的刚度指标以保证不出现过大的变形。在路面强度方面，国际通行的设计指标[6]主要为沥青层拉应变和路基压应变。

路面设计弯沉值ld按式(1)确定[7]。

(1)

式中：ld为设计弯沉值，0.01 mm；Ne为设计年限内一个车道累计当量轴次；Ac为公路等级系数，高速公路、一级公路为1.0，二级公路为1.1，三、四级公路为1.2；As为面层类型系数，沥青混凝土面层为1.0；热拌和冷拌沥青碎石、上拌下贯或贯入式路面、沥青表面处治为1.1；中、低级路面为1.2；Ab为基层类型系数，对半刚性基层Ab=1.0，柔性基层Ab=1.6。

沥青混凝土层、半刚性基层和底基层以拉应力为设计或验算指标时，材料的容许拉应力σR按式(2)计算。

(2)

式中：σR为路面结构层材料的容许拉应力，MPa;σS为沥青混凝土或半刚性材料的极限抗拉强度，MPa；KS为抗拉强度结构系数。

本文中沥青路面累计当量轴次(BZZ-100)为2.08×107，计算得到沥青路面设计值见表1。

表1 沥青路面的设计指标容许值

2 温度-车辆荷载作用下沥青路面力学响应

2.1 沥青路面三维有限元模型

沥青路面结构组合见图1，基本假设如下：①各层为均质的各向同性的线弹性体；②各层之间的接触面为完全连续，且不发生相对滑动；③不计路面结构自重影响；④不考虑温度沿道路纵向分布，认为在同一时刻、同一水平面上温度处处相等，忽略接触热阻，假定层间温度和热流连续，材料热参数为常数。

根据上述假设及有限元分析原理，利用AN-SYS有限元软件建立沥青路面三维有限元模型，模型几何与材料参数见表2、表3，为简化分析，假定路面材料力学及热学参数不随温度变化。模型边界条件假设为：土基底面全部约束，左、右两面X方向约束，前、后两面Z方向约束，面层表面为自由面。其中X为行车方向，Z为路面横向方向，Y为垂直于路面向上方向。车辆荷载分析采用SOLID45单元，热分析采用SOLID70单元，模型采用映射网格划分，沥青路面的三维有限元模型见图2。

图1 沥青路面结构组合(单位：cm)

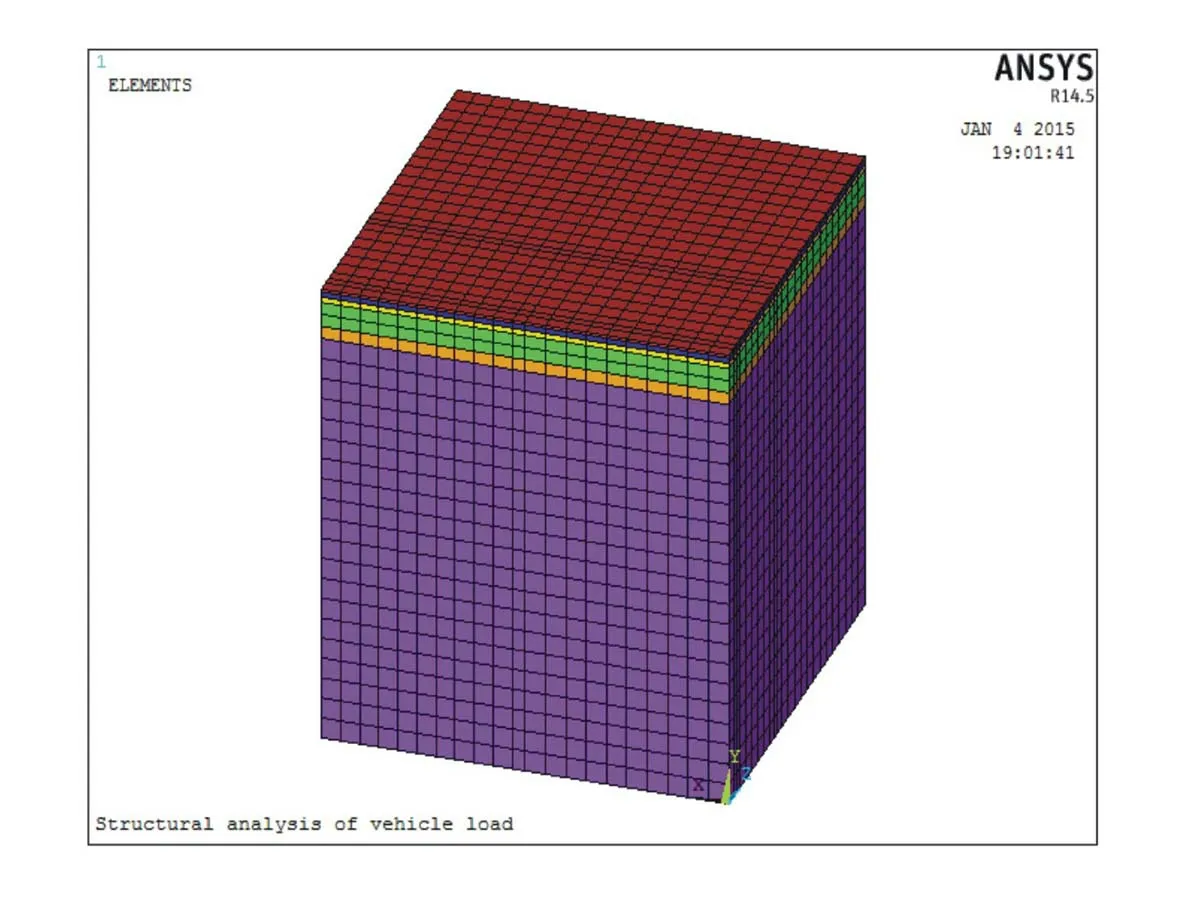
图2 沥青路面有限元模型

结构层长度/cm宽度/cm厚度/cm弹性模量/MPa泊松比线膨胀系/(×10-6·℃-1)上面层SMA-1360060041 3850.2820水泥乳化沥青混凝土联结层60060082 8000.2710半开级配过渡基层AM-256006008 7200.3025水泥稳定碎石基层600600361 5500.159水泥稳定碎石底基层600600181 4800.159土基600600600500.3550

表3 沥青路面材料热学参数

2.2 车辆-温度耦合荷载下沥青路面力学响应

车辆荷载采用标准轴载BZZ-100，轮胎标准内压0.7 MPa，2轮间距为32 cm，轴距为182 cm，单轮荷载简化为矩形18.9 cm×18.9 cm，接触面积为357.21 cm2，双轮边缘间隙13.1 cm，两侧边缘间隙131.1 cm，见图3。车轮加载最不利位置[8]见图4。

图3 轮胎与路面接触等效示意图(单位：cm)

图4 车轮加载最不利位置图(单位：cm)

沥青路面结构表面上存在的热交换主要有3种传递方式，即热传导、热对流和热辐射，路面结构内的热交换遵守热传导平衡方程。以路表温度和热对流系数为边界条件，使热量在路面各结构层之间相互传递。其边界条件简化为包括太阳总辐射的日过程、外界气温的日过程、路表面及道路基底的温度估算。太阳总辐射的日过程和外界气温的日过程根据国同济大学严作人[9]提出的函数形式近似模拟。天气条件参数取自文献[10]，当土基达到一定深度时，其温度变化可以看成常数，地基底面低温约束为20 ℃。本文路面模型的初始温度设定为20℃，与上午06：00的近地温度相同，采用瞬态热分析方法，计算出沥青路面温度随时间变化曲线，见图5。

图5 沥青路面温度-时间变化曲线

计算结果表明，路面结构深度对温度变化的影响十分明显，随着路面结构深度的增加，外界温度对路面结构的影响越来越小，这也是结构存在温差的主要原因。

为了将问题简化，假设各层材料均匀、完全弹性且各向同性，层间接触良好，温度函数满足连续条件；忽略路面结构自重影响；温度变化范围内，路面各结构层材料热学参数保持恒定。温度应力分析计算模型的边界条件为：模型的底面完全约束，左、右2个面垂向约束，即行车方向的两面约束。本文研究升温过程中产生的温度应变，因此根据计算的温度场结果，将路面各结构层的0应力参考温度设为20 ℃。 沥青路面24 h内升温过程下，沥青路面各层层底拉应变变化曲线见图6。

图6 升温过程中沥青路面各层层底拉应变变化曲线

由图6可见，升温过程中沥青路面上面层、过渡基层层底拉应变随温度变化较明显。上面层层底在14：00达到最大拉应变；过渡基层在20：00达到最大拉应变。

综上，温度荷载对沥青路面有很大影响，不容忽视，特别是上面层，其最不利最大温度应变可能会超过其极限值。

根据前文计算的温度场结果，模拟升温过程温度-车辆耦合荷载作用下沥青路面力学响应。沥青路面升温过程中温度-车辆耦合作用下各指标变化曲线见图7。

图7 温度-车辆耦合荷载作用升温过程各指标变化曲线

2.3 分析与讨论

对于常见的沥青路面结构，文献[11-12]提出沥青层底拉应变不大于120×10-6、土基顶面压应变不大于280×10-6的结论，该结论是在基于普通沥青类材料且没有考虑温度影响的情况下提出的。本文分析表明，温度对沥青路面的上面层影响较为明显，温度效应下,上面层层底的最大拉应变约为车辆荷载作用下的2.5倍，而且可能大于材料容许的拉应变。

由于温度效应下，沥青路面上面层层底拉应变、过渡基层层底拉应变变化较为明显。故作上面层、过渡基层最大层底拉应变，土基顶面最大压应变,路表弯沉值在3种荷载效应下与其容许值的柱状对比见图8。

图8 沥青路面3种荷载效应作用下各控制指标对比

由图8可见，温度效应单独作用下上面层最大拉应变为270×10-6，占温度车辆耦合作用下的77%，故升温对沥青路面上面层层底拉应变影响很大；土基顶面最大压应变在温度-车辆耦合荷载作用下，相对于车辆荷载单独作用减少了17×10-6(由于升温土基顶面产生的是拉应变)，即7.4%，故升温对沥青路面土基顶面压应变影响较低。

另外，在三维有限元模型中，车辆荷载单独作用下路表弯沉值已远大于规范的容许值，所以按照二维层状体系理论求得的路表容许弯沉值不适用于作三维模型的容许值。升温过程中路表弯沉值为负值，是因为升温使路面膨胀，温度-车辆耦合作用下路表弯沉值相对于车辆荷载单独作用下减小了20.5×10-6，即48.2%，故升温对沥青路面弯沉值影响较大。

3 结语

1) 最不利温度荷载对沥青路面结构影响很大，其升温过程中上面层层底最大拉应变为270×10-6，约是车辆荷载作用下的2.5倍。最不利温度荷载对沥青路面的弯沉值影响较大,对土基顶面压应变影响较小。

2) 温度-车辆耦合荷载对沥青路面路面影响不容忽视，其中温度荷载对上面层层底拉应变会产生很大影响,其最不利温度应变和耦合应变会超出其容许应变，建议在沥青路面设计指标中考虑温度效应的影响。

3) 通过分析温度荷载对沥青路面结构的影响可以看出，温度荷载对沥青路面上面层层底拉应变影响很大，夏季高温环境下应注重对沥青路面的洒水养护。

4) 本文只模拟了沥青路面在最不利温度荷载作用下升温过程的力学响应，对于降温过程的力学影响规律还有待探讨。