引黄灌区水资源配置的多目标耦合优化分析

杨喜春

(内蒙古绰勒水利水电有限责任公司，内蒙古 呼和浩特 010010)

近年来，引黄灌区在水资源供需、泥沙淤积和土壤盐碱化等方面的问题日益突出，能否综合考虑水资源、经济和环境之间的关系，实现灌区持续健康发展成为研究的热点。合理配置水资源，使有限的水量发挥其最大的效益，对于灌区的可持续发展具有重要意义。

如何科学地进行水资源配置，提高水资源的利用率，一直是水文水资源研究的难点。对于灌区水资源的优化配置，Divakar L等人[1]优化了湄南河流域的水资源配置，并设计了程序；李彦刚等人[2]以效益为目标对宝鸡峡灌区的水资源利用率进行研究；许晓华等人[3]通过对位山灌区泥沙淤积的研究，提出其对生态环境的影响以及解决措施；胡春宏等人[4]提出将泥沙与水资源联合的配置方式；杨思存等人[5]对甘肃引黄灌区土壤的盐渍化特性进行了典范对应分析。然而，这些方法对于水资源、泥沙和盐碱化问题的研究属于单方面或2方面的居多，而对于多目标的联合研究较为少见。本文采用分层序列的方法对3个模型进行耦合，对小开河灌区水资源进行优化配置，在保证经济效益和用水可靠性的前提下，提高水资源的利用率和环境效益，为灌区的水资源配置提供科学依据。

1 研究区域概况

小开河灌区位于山东省北部，覆盖2区4县，实际灌溉面积7.67万hm2，灌区上游处于鲁北淡咸区，下游处于鲁北滨海区，地下水资源匮乏，年开采量0.0536亿m3，地表水利用量0.11亿m3。发展引黄灌溉以来，每年的引水量接近2亿m3，灌区干渠全长91.5km，其中输沙渠51.3km，沉沙池位于灌区中游，采用大比降远距离输沙，对于改善灌区环境意义重大。但随着黄河水资源的紧缺以及自身需求量的增加，长期引黄带来的土地次生盐碱化[6]、渠道泥沙淤积等成为制约灌区可持续发展的重要因素。

2 模型建立

根据小开河引黄灌区实际存在的问题，参考国内外灌区水资源配置的可靠方案，在考虑未来发展趋势的前提下，从水资源供需效益、泥沙长距离输运和地下水埋深3个方面建立模型。在保证模型准确性的同时对问题进行适当简化，降低复杂模型的求解难度和对数据精准性的要求，提高其实用性和普遍性。

2.1 水量模型

水资源的供需矛盾作为引黄灌区的常见问题，需通过确定各子区在各时段的各类引水量以及各行业的分配比例与方式，对水资源进行合理分配和利用，在满足约束条件的情况下建立水量模型。

2.1.1 目标函数

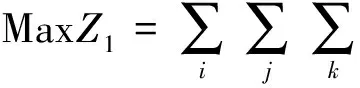
(1)

式中，Wdi，j，k，Wri，j，k，Wgi，j，k—k时段i子区内j行业的地表水，地下水和引黄水的使用量；αi，j，βi，j，γi，j—i子区内j行业的引黄水，地表水和地下水的利用净效益；引水时段以月计，并以经济效益作为最大考量指标。其中，小开河灌区的水资源包括地表水、地下水和引黄水，其中引黄水为主；用水区域为开发区、滨城区、阳信县、沾化县、惠民县和无棣县；用水行业主要为农业、工业和生活。

2.1.2 约束条件

水量平衡约束，即各子区各行业所使用的引黄水量之和应等于各子区的有效引黄总量：

(2)

供水量约束，即各时段的引水总量应不大于3个水源的可供水量：

(3)

需水量约束，即分配到各行业的水量应介于该行业最低与最高需水量之间：

Di，j，k≤Wri，j，k+Wdi，j，k+Wgi，j，k≤Gi，j，k

(4)

非负约束：

Wdi，j.k≥0，Wri，j.k≥0，Wgi，j.k≥0

(5)

式中，Wtk—k时段的引黄总量;ηi—i子区的渠道利用系数;LWdk—k时段引黄水的上限值;TWy—全年有效引黄水总量;LWri，k，LWgi，k—k时段i子区地表和地下水的上限值;Di，j，k，Gi，j，k—k时段i子区j行业最低和最高需水量。

2.2 泥沙模型

引黄河的同时也会造成泥沙的淤积，根据毛伟兵等人[7]的研究，小开河地区由于条件限制，长距离输沙的方式较为合适。利用2个目标函数和约束条件来建立泥沙模型，从而达到减少淤积的目的。

2.2.1 目标函数

当黄河水含沙量较低时，引水量的比例应加大；同时引水量较小时，应优先满足上游的用水单位。根据黄河多年来各月的流量和小开河引黄闸每月的含沙量统计，将2个目标结合起来考虑，即弱化中上游区域低含沙期的作用，强化高含沙期的影响，从而达到降低高含沙期引水量，又能尽量分布在中上游的目的。

(6)

式中，π—调节系数，取0.05～0.5；Ω和Π—少含沙月份集和上游区域集。

2.2.2 约束条件

最低流量与引水能力约束：

(7)

式中，htk—k时段的引水时间;Ld—最大设计流量;Resi—i子区的最大引黄能力。

2.3 地下水模型

小开河引黄灌区地下水环境在各个子区的情况不同，但基本不存在超采漏斗和咸水入侵的问题，需注意长期引黄而不抽取地下水造成的土壤次生盐碱问题。合理控制地下水位的深度在3～6m对农作物的生长最为有利。

2.3.1 目标函数

(8)

式中，msi，k—k时刻i子区的地下水深度。

2.3.2 约束条件

地下水的水位随着进去和损失的水量而变化，不考虑灌区各子区内地下水水平方向上的交换，根据水量平衡得出地下水水位深度：

msi，k+1=msi，k-[ωi·Pi，k·F+(Wdi，1，k+Wri，1，k)

(ξi+σiρi)+Wgi，1，k(θi-1)]/μiFi+ETi，k

(9)

式中，ωi—降雨补给系数;pi，k—降雨量;F—区域面积；j—农业用水，j=1;ξi和ρi—渠系和灌溉入渗补给系数;σi—渠系水利用系数；θi—井灌回归补给系数；μi—给水度；ETi，k—地下水蒸发强度。

地下水深度下限：msi，k≤6。

3 计算结果与分析

由于各模型间的量纲不同，无法公度而进行直接求解，因此采用分层序列法进行多目标的耦合求解。先对水量模型进行求解，将其结果按80%的控制指标转化为约束条件，合并入泥沙模型进行二次求解，将得到的结果同样合并入地下水模型求解，最终得到3个模型耦合而成的最优解。

多目标耦合的模型综合考虑了水资源配置所带来的经济、泥沙以及地下水环境效益，各层次求解的配置结果见表1、2。可以看出，随着逐层求解，配置效果逐步均衡，其中经济效益虽略有下降，但保持在最优值的95%左右；水沙目标有一定提高；地下水目标则不断改善，最终达到42%的优化效果。

表1 50%水平年的水资源配置结果

表2 75%水平年的水资源配置结果

不同水平年水资源最终的具体分配方案见表3、4，其中各类用水中水资源依次为地表水、地下水和引黄水。可以看出，在不同的水平年份，所分配的总水量均低于可供水量，其中引黄水占主要部分，引黄水资源的利用率达到80%，同时50%和75%水平年分别有868.68万和705.94万m3剩余水量，对于水资源的节约和灌溉面积的扩大具有明显效果。

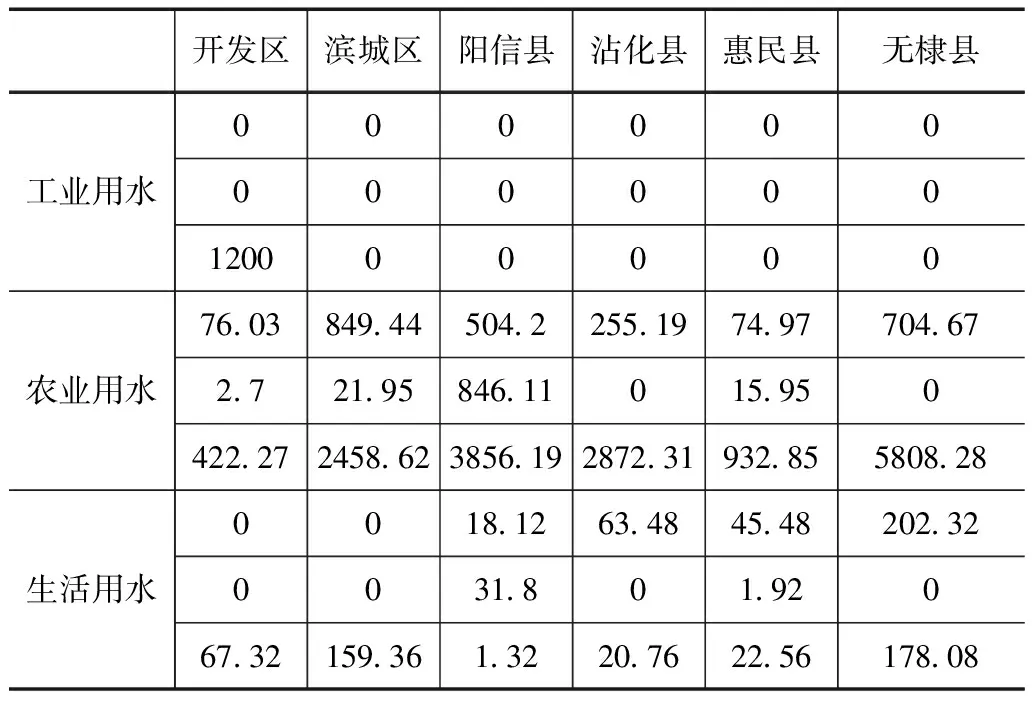
表3 50%水平年水资源最终的分配方案 万m3

表4 75%水平年水资源最终的分配方案 万m3

4 结语

基于水量、泥沙和地下水模型的多目标耦合模型，对小开河引黄灌区的水资源配置进行优化分析，配置方案更加均衡，经济效益可保持在95%的范围内，水沙和地下水指标均有明显提升。同时，50%和75%水平年的水量均有剩余，提高了水资源的利用率和用水的保证率，扩大了灌溉面积。表明该模型的合理性与可靠性，为小开河引黄灌区的水资源配置提供科学依据。