负载参数对微型摆式内燃机的影响机制分析
余 海,史 波
(南京航空航天大学 能源与动力学院, 南京 210016)
2005年,美国巴特勒研究所在一项研究报告中列出了预计到2020年的10个最具战略意义的技术趋势[1],其中位居第二位的是大功率能源装置,包括先进电池、廉价燃料电池和微型发电机等的开发。微型发电机在微型电脑、便携式检测仪器和微型机器人等微型机电设备有着广阔的应用前景。目前机电设备的微型化发展迅速,对能量需求也越来越高。在过去的20年里,微型机电设备的能量需求增加了约20倍,但常规的便携式电源(化学电池)的能量密度只增加了3倍,化学电池的有限能量密度限制了微型机电设备的进一步发展。
基于碳氢燃料的内燃机是化学电池的替代产品之一,理由如下:碳氢燃料具有很高的能量密度(50 MJ/kg),是化学电池的50倍左右[2];碳氢燃料与电池相比具有容易运输、易存储和环境污染小的优点;内燃机具有较高的能量转化效率。因此,内燃机微小型化成为微型能源发电系统的一个重要研究方向。自20世纪90年代,微型涡轮机[3-4]、微型转子发动机[5]、微自由活塞发动机[6]、微型摆式内燃机[7]相继被提出。研究发现,这些微型内燃机的能量密度普遍较高,以微型燃气轮机为例,其能量密度可达1 100 MW/m3[2]。
微型摆式内燃机[7]由密歇根大学在2000年率先提出,该内燃机具有结构简单、易于加工与组装的优点。之后,国内外高校如佐治亚理工学院[8]、清华大学[9]、上海交通大学[10]、浙江大学[11]、南京航空航天大学[12]、中科院工程热物理研究所[13]与广州能源研究所[14]等科研单位均围绕微型摆式内燃机/发电系统开展了大量理论与实验研究。笔者通过研究发现,质量负载和电磁负载可以显著影响微型摆式内燃机的性能。基于此,本文针对质量负载和电磁负载对摆式内燃机的影响展开研究,并通过优化算法,考虑泄漏、传热和摩擦损失以模拟实际工况,计算出指示功率和热效率的最大值。
1 物理模型
参考密歇根大学团队研究的微型摆式内燃机结构尺寸与运行工况参数[7],本文所研究的微型摆式内燃机模型如图1所示。气缸腔内整体直径为45.7 mm,气缸厚度为15 mm,腔体角度为120°。该系统为四冲程热力循环,任意时刻各个腔都处于互不相同的行程。当摆臂完成1次摆动时,分别有2个腔体积膨胀,2个腔体积缩小,对应于1次燃烧(膨胀)、压缩(缩小)、进气(膨胀)和排气(缩小)。
本文采用异丁烷作为燃料,空气作为氧化剂,采用Matlab编程进行仿真。内燃机的几何尺寸及运行工况参数如表1所示。
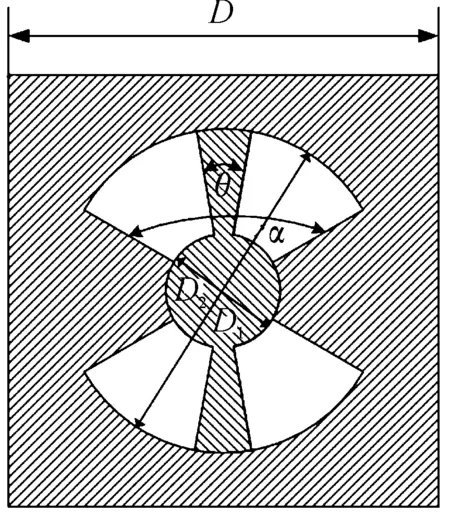
图1 微型摆式内燃机模型

参数/单位数值备注D/mm61整机外径D1/mm45.7内燃机直径D2/mm16轮彀直径D3/mm15气缸厚度α/(°)120大气缸夹角β/(°)20摆臂夹角ϕ0.8当量比Tw/K800气缸内壁温Cd0.7流量系数d/mm3进排气阀门直径τ/ms2.5燃烧时间H/μm10泄漏间隙Tf/(N·m)0.1摩擦力矩
2 数学模型
2.1 腔内工作过程基本方程
工质模型有气体状态方程、质量守恒方程、能量守恒方程和组分质量守恒方程,其通用形式为
▽(ρμφ)=▽(ζφ▽φ)+S
(1)
式中:φ为通用变量;ζφ为广义扩散系数;S为广义源项;ρ为密度;μ为速度。
四冲程摆式内燃机的动力学平衡方程[7]为
式中:I0为中心摆的转动惯量;J为质量负载;θ为摆臂的摆动角度位置;Δp为相邻腔室压力差;AS为工质压力作用于摆臂的有效压力面积;LR为工质在摆臂上的平均作用点到中心轴的距离;K为发电机作用于内燃机的电磁负载;Tf为作用于摆臂的摩擦阻力矩,作用方向保持与摆臂运动方向相反。
控制体积内温度和压力导数表达式[7]为:
由于微型内燃机实际燃烧过程复杂,故目前还不能对燃烧规律进行准确描述,就研究现状而言采用韦伯方程模拟实际燃烧过程是可以接受的。周雄等[15]基于韦伯方程研究燃烧时间对微型摆式内燃机性能和热力学过程的影响,研究结果表明燃烧时间作为燃烧变量是可以接受的。因此,本文燃烧模型采用韦伯燃烧模型,并将燃烧时间设置为2.5 ms。
本文气体与腔体间的传热为实时换热过程,其中瞬时对流换热系数采用Annand Correlation[16]进行计算。
Zhou等[13]基于实验得出了微型摆式内燃机的精确泄漏模型。因此,本文采用Zhou等[13]得出的泄漏模型来描述气体在腔体之间的泄漏过程,并将泄漏间隙设置为10 μm。
目前,准确的摩擦经验公式难以建立,且摩擦损失相对传热损失和泄漏损失来讲对微型摆式内燃机的影响很小。因此,徐建华等[12]在微型旋转摆式发动机的分析中只考虑了传热和泄漏的影响,忽略了摩擦对性能的影响。本文将实验样机装配完成后,用扭矩扳手测得此时中心摆的摩擦阻力矩(约为0.1 N·m),故本文摩擦阻力矩设置为0.1 N·m。
2.2 进化算法模型
进化算法采用粒子群算法[17]。该算法以容易实现、精度高、收敛快等优点引起了学术界的重视,并在解决实际问题中展示了其优越性。
粒子群算法的公式为
xi=xi+vi
(6)
3 结果与讨论
采用Matlab编程进行仿真计算,同时求解2.1节所有的微分方程,直至收敛,此时所得参数均为稳态工况的参数。燃烧过程用韦伯燃烧放热规律描述,并考虑传热损失、泄漏损失和摩擦损失对微型摆式内燃机的影响。
3.1 负载对系统的影响
质量负载J和电磁负载K的取值范围在表2给出,其他参数均见表1。
在图2、3中的压缩止点处存在的“打结”现象是间隙泄漏所致。泄漏效应越强,表明打结程度越深。就理想OTTO循环而言,压缩比越大,热效率越大。
如图2所示,质量负载J越大,压缩过程中压力曲线越高,打结程度越来越深,表明泄漏损失增强;燃烧过程越来越接近理想OTTO循环,表明燃烧损失降低。由图4可知:质量负载越大,压缩比越大,循环的热效率提高。因此,必然存在适中的质量负载使压缩比ε较高,而泄漏损失和燃烧损失较小,从而使热效率最大。
如图3所示,电磁负载K越大,压缩过程中压力曲线越低,打结程度越来越轻,表明泄漏损失降低;燃烧过程越来越接近理想OTTO循环,表明燃烧损失降低。由图4可知:电磁负载越大,压缩比越小,循环的热效率降低。因此,必然存在适中的电磁负载使压缩比ε较高,而泄漏损失和燃烧损失较小,从而使热效率最大。
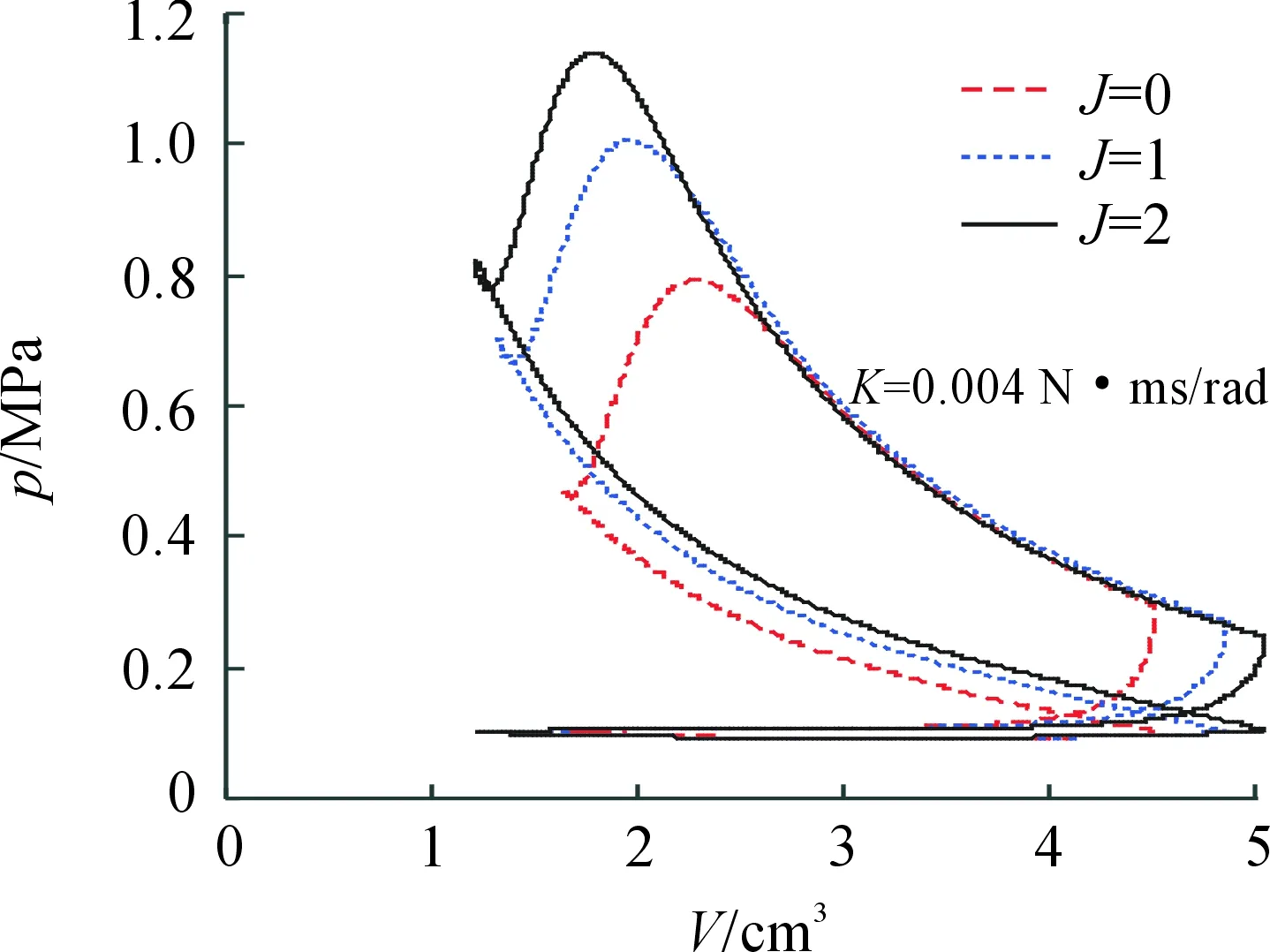
图2 固定电磁负载时,不同质量负载J对单个腔室循环p-V的影响 (电磁负载K=0.004 N·ms/rad)

图3 固定质量负载时,不同电磁负载K对单个腔室循环p-V的影响曲线(质量负载J=1)

图4 不同质量负载J下,电磁负载K对压缩比ε的影响
质量负载和电磁负载对摆式内燃机的定量结果见图5、 6。如图所示,固定质量负载,当电磁负载从0.001 N·ms/rad增加到0.005 N·ms/rad时,系统的指示功率P和热效率η均先增加至最大值,随后下降。当电磁负载小于0.002 N·ms/rad时,J越小则热效率和指示功率越高;电磁负载大于0.005 N·ms/rad时,J越大则热效率和指示功率越高。这表明存在适中的质量负载J和电磁负载系数K,使得指示功率P和热效率η各自取得最大值。
如图5、6所示,质量负载J=0时,电磁负载在0.003 N·ms/rad处时热效率取得最大值;质量负载J=1时,电磁负载在0.004 N·ms/rad处时热效率取得最大值;质量负载J=2时,电磁负载在0.005 N·ms/rad处时热效率取得最大值。这表明质量负载的增加会提高内燃机的电磁负载的带载能力。

图5 不同质量负载J下,电磁负载K对指示功率P的影响
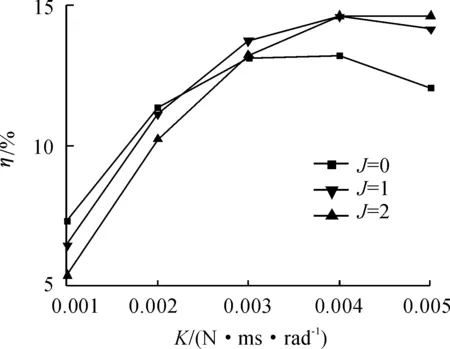
图6 不同质量负载J下,电磁负载K对热效率η的影响
3.2 优化算法计算结果
由前文知,负载显著影响系统的指示功率和热效率,因此可以通过改变负载的数值来提高压缩比,抑制泄漏损失和燃烧损失,从而得到最优的功率和热效率。本文引入粒子群算法(模型在2.2节给出),并考虑传热损失、泄漏损失和摩擦损失对系统性能的影响,以质量负载和电磁负载作为变量,其他参数保持不变(见表1),计算热效率和指示功率的最大值。
图7中,每代种群有25个粒子,经过50代得出热效率最优值进化曲线。经过50代后,热效率已经收敛。此时热效率的值η=16.7%,对应的质量负载J=1.49,电磁负载K=0.004 57 N·ms/rad。图8中,每代种群有25个粒子,经过50代得出指示功率最优值进化曲线。经过50代后,指示功率已经收敛。此时指示功率的值P=243.3 W,对应的质量负载J=0.44,电磁负载K=0.002 81 N·ms/rad。

图7 最佳热效率η进化曲线

图8 最佳指示功率P进化曲线
4 结束语
本文建立了微型摆式内燃机的零维模型,研究了质量负载和电磁负载对系统性能的影响机制。通过研究发现,质量负载越大,则泄漏损失加剧,燃烧损失减小,压缩比增加;电磁负载越大,则燃烧损失降低,泄漏损失降低,压缩比减小。因此,存在适中的质量负载和电磁负载系数,使得指示功率和热效率各自取得最大值。同时,质量负载的增加会提高内燃机的电磁负载带载能力。本文利用优化算法,考虑泄漏、传热和摩擦损失以模拟实际工况,得出的热效率和指示功率的最大值分别为16.7%和243.3 W。
——内燃机4.0 Highest Efficiency and Ultra Low Emission–Internal Combustion Engine 4.0

