移动平均期数对农产品供应链成本及牛鞭效应的影响

杨宏斌

（河南财政金融学院 经济与法律学院，郑州 450046）

0 引言

在供应链管理实践中，交货提前期内产品的销售情况存在不确定性，供应链成员企业为了能够制订科学的订货策略，需要针对提前期和提前期内产品的需求情况进行预测，基于根据预测的提前期和产品需求情况确定适当的期望库存。移动平均法是供应链成员常用来进行产品需求预测的一种方法，通过选取企业产品过去不同时段销售数据进行预测，确定订货提前期内产品需求的期望值，所以，有必要对移动平均方法期数的选择问题进行探究。

在农产品供应链管理中，农产品的需求预测影响着农产品经销商的订货批量、价格策略和订货周期等行为，上述决策的失误往往会导致农产品销售出现积压甚至变质，大大影响农产品经销商乃至整个农产品供应链的利润。对农产品供应链管理中移动平均预测方法的期数选择的研究，一方面丰富了现有农产品供应链管理的文献成果，另一方面为农产品供应链成员企业提供决策依据，提升农产品供应链绩效，具有重要的理论价值和实际意义。

本文基于系统动力学理论和借助Porwersim2005软件，构建了一个三级农产品的供应链模型，针对模型中移动平均预测方法平均期数的不同取值对农产品供应链牛鞭效应现象和成本的影响及两者之间的关系进行了分析，探究移动平均期数、供应链成本、牛鞭效应之间的因应规律，旨在对农产品供应链绩效的优化问题提出对策，为农产品供应链成员企业提供决策参考。

1 模型构建

本模型供应链成员采用简单移动平均法进行预测。

一次简单移动平均值的计算公式为：

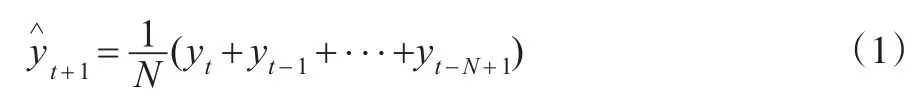
为了研究移动平均方法期数不同取值分别对供应链牛鞭效应现象、供应链成本的影响以及两种之间的关系，构建出三级农产品供应链成本模型，见图1所示。

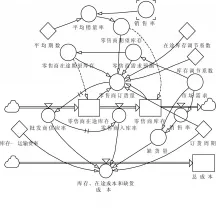
图1 研究模型

本文的移动平均预测系数的取值在1～7之间。图2为批发商的期数为7（N=7）的一次简单移动平均法的系统动力学模型。

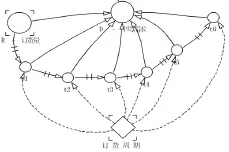
图2 批发商移动平均预测方法的系统动力学模型

图2模型中相关变量设置为：批发商D的平均需求量=AVERAGE('R-订货量'，t1，t2，t3，t4，t5，t6)/TIMESTEP；其中t1，t2，t3，t4，t5，t6分别表示移动平均期数为2天，3天，4天，5天，6天，7天。

零售商R的订货量=PULSE(零售商订货量,START-TIME+0＜＜da＞＞，订货周期)；订货周期=3＜＜da＞＞；t1=DELAYPPL('R-订货量'，订货周期)；t3=DELAYPPL(t2，订货周期)；t6=DELAYPPL(t5，订货周期)。

2 仿真数据分析

2.1 移动平均期数对农产品供应链成本的影响分析

基于上述模型，分别对移动平均期数取1～7天对上面移动平均法的系统动力学模型进行仿真，以对移动平均方法期数的变化对供应链需求波动幅度的影响进行分析。仿真汇总后的数据见表1所示。

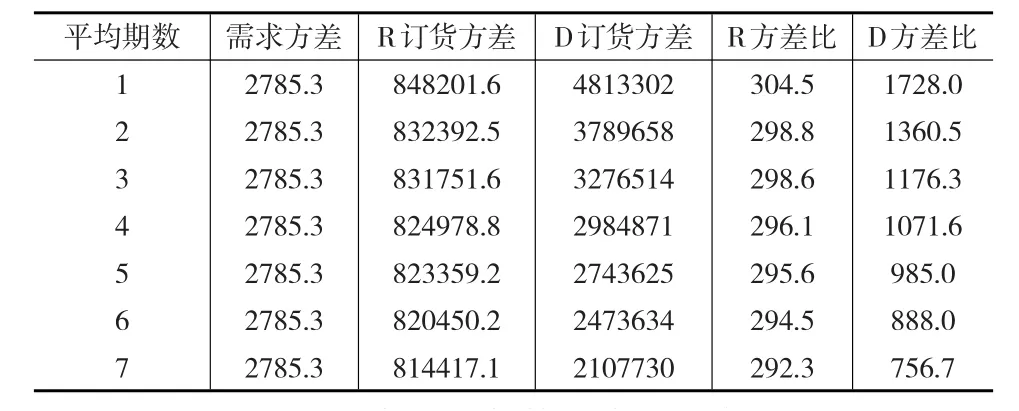
表1 移动平均期数变化对牛鞭效应的影响

由表1可知，移动平均期数的变化对供应链需求波动存在影响，当移动平均期数增大时，即由1至7时，供应链成员零售商R、批发商D乃至整个供应链需求波动程度（牛鞭效应）呈现出减弱的趋势。

图3 不同移动平均期数下供应链需求波动图

图3直观的描述了不同移动平均期数值下供应链需求波动的变化趋势。零售商采用移动平均方法，选取近期历史商品销售数据进行下一期的需求预测，其订货量的方差则呈现较平稳且略有减弱，同样，批发商则根据零售商过去几次的订货数据进行下一期需求预测，批发商的订货量方差则呈现较强烈。基于上述现象的合理解释是，以批发商情况为例，由移动平均预测技术相关理论知道，移动平均期数在预测中起着对历史观测值的“拉平”作用，当移动平均期数选择比较大时，假如移动平均期数为7，此时批发商根据下游零售商近期7次的订货数值作为预测依据进行平均，与移动平均期数为6的平均值相比，预测结果则更平均，这样，就多次预测结果的需求波动程度则表现更小，在确定订货量时，如果其他条件不变，批发商选取的移动平均期数越多，需求预测结果和下游零售商订单需求的整体变化趋势越一致，批发商由大移动期数产生的“平稳”预测值则形成“平稳”的期望库存目标，最终形成“平稳”的订单，这又形成上游制造商较为“平稳”的产品供给量，此时，与小的移动平均期数下的预测结果形成的订货量相比，供应链成员需求波动则表现较弱，也就是说，当满足自己需求的条件时，供应链下游成员越是采用“拉平”式的订货策略（采用较大的移动平均期数），则牛鞭效应现象表现得（越）弱。

对不同平均期数下，表2是对批发商D根据下游零售商R的最近的历史订单数据产生的移动平均预测信息进行的汇总，结果与上述的成因分析一致。

表2 不同期数下批发商D基于零售商R订单的移动平均值

2.2 不同移动平均期数下农产品供应链成本与牛鞭效应间的关系分析

移动平均期数下供应链牛鞭效应现象与供应链库存总成本之间的关系，见表3所示。随着移动平均预测期数的增大，供应链成员的订单越表现平稳，供应链下游企业采用多期的历史产品销售数据来制订期望库存目标有助于减弱供应链成员需求波动程度，供应链总库存成本呈现减少的趋势；移动平均期数较小，供应链需求波动则表现出比较强烈，同时，供应链总库存成本也比较高。

表3 移动平均期数下的供应链库存的总成本

进一步研究预测准确性、供应链库存总成本和需求波动性三者的关系。由模型仿真和移动平均公式可以得到零售商不同预测期数下的预测值及预测值的标准误（令T=14）。仿真收集或统计计算后的数据汇总见表4。

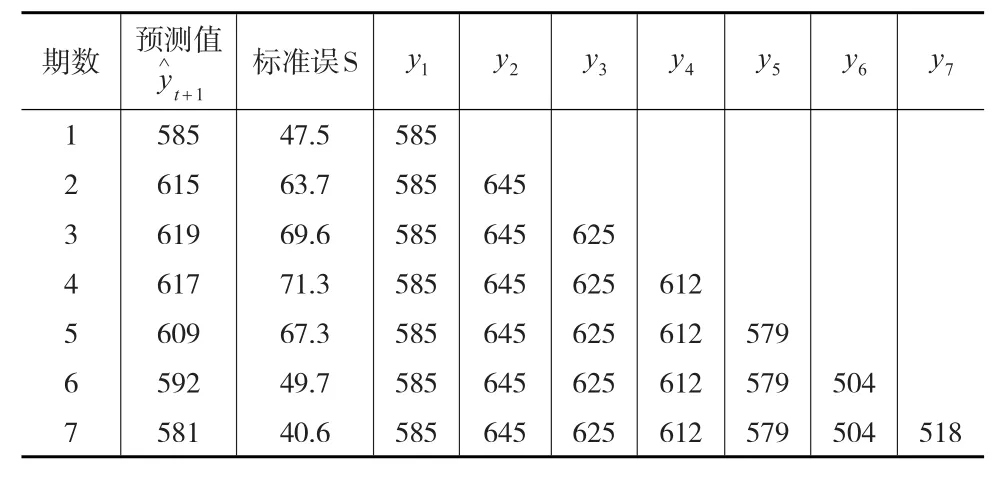
表4 零售商不同预测期数下的预测值及预测值的标准误

由表4可以知道，当平均期数N=7时，标准误差S=40.6，为诸多标准误差值中的最小值，结合上述移动平均法知识可知，此时，移动平均预测方法准确性最高；由表1可以看到，随着移动平均期数N的增大，供应链需求波动性呈现减弱趋势；又由表3可知，供应链库存总成本随着移动平均期数N的增大而减少。综合上述数据分析可知，供应链需求的精准预测有助于减弱需求波动程度（牛鞭效应）、减少供应链库存总成本。

3 结论

本文借助软件Porwersim2005构建了三级农产品供应链模型，基于移动平均需求预测方法的平均期数不同取值分别对供应链牛鞭效应现象、供应链成本的影响以及两种之间的关系进行了分析。主要结论如下：

平均期数对历史需求数据起到“拉平”的作用，当移动平均期数增大时，供应链成员零售商R、批发商D乃至整个供应链需求波动程度（牛鞭效应）呈现出明显的减弱趋势。当满足自己需求的条件时，供应链下游成员越是采用“拉平”式的订货策略（采用较大的移动平均期数），则牛鞭效应现象表现得（越）弱，供应链需求的精准预测有助于减弱需求波动程度（牛鞭效应）、减少供应链库存总成本。

在供应链管理实践中，管理者需要对未来需求努力做出科学精准的预测；选择合适的移动平均期数，制订合理的期望库存目标和订货策略，有助于帮助供应链成员企业降低库存成本，有助于减弱供应链需求波动、提升供应链绩效管理水平。