不同土质下耕刀工作的离散元受力仿真分析

刘超颖，张 旭，李晨阳，吴文江，王振兴

(1.河北中医学院，石家庄 050020；2.石家庄铁道大学 a.机械工程学院；b.工程训练中心，石家庄 050043；3.北京铁路局 天津机务段，天津 300011)

0 引言

耕刀是旋耕机的主要工作部件，由于其转速快、瞬时撞击力大及与土壤接触时接触机理复杂等原因，直接影响了旋耕机的旋耕效果、能量消耗及功率分配等，因此研究耕刀在不同土质下的动力学问题具有重要意义。通常情况下，机械-土壤使用接触模型方法多为分析法[1]、经验法[2]、连续体数值法[3]，但对于分析沙土等介质均有着明显的不足[4]。本文以小型旋耕机的一组耕刀为研究对象，应用Hertz模型建立耕刀切割土壤的离散元模型[5-7]，针对不同能量粘结键的土壤进行旋耕实验，以旋耕效果为依据获取较为理想的粘结键能量值和耕刀的受力情况。针对单一DEM法中机械部件被视为面单元，无密度、质量、转动惯量等物理参数，会造成接触失真，采用EDEM和ADAMS的动力学耦合来解决，以得到精细的动力学状况。本文研究成果不仅适用于旋耕刀具，对工程土方机械、掘进机械、矿山机械等机械结构的优化改进也具有指导性意义[8-10]，具有广阔的应用前景。

1 机械模型

研究对象为小型农用旋耕机，主要结构包括控制把、动力与传动装置、护板、旋耕刀、旋耕深度控制盘和可调试支撑悬挂，如图1所示。以一组旋耕刀为例，其刀具的尺寸示意图如图2 所示。单组耕刀具有4把耕刀，耕刀长度为230mm，耕刀的最大旋耕深度为68mm，单组耕刀耕副为100mm；4把耕刀由螺栓固定在刀架上，耕刀的材质为耐磨、高强度的65锰钢。

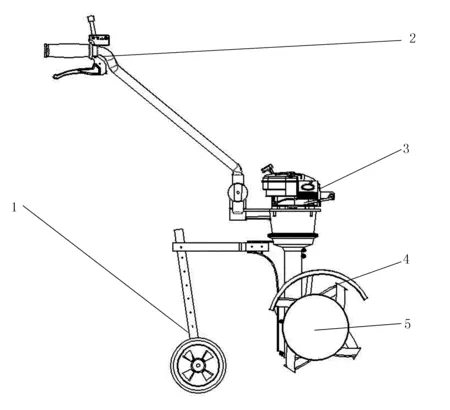
1.支撑悬架 2.控制把 3.动力装置 4.耕刀 5.深度控制盘

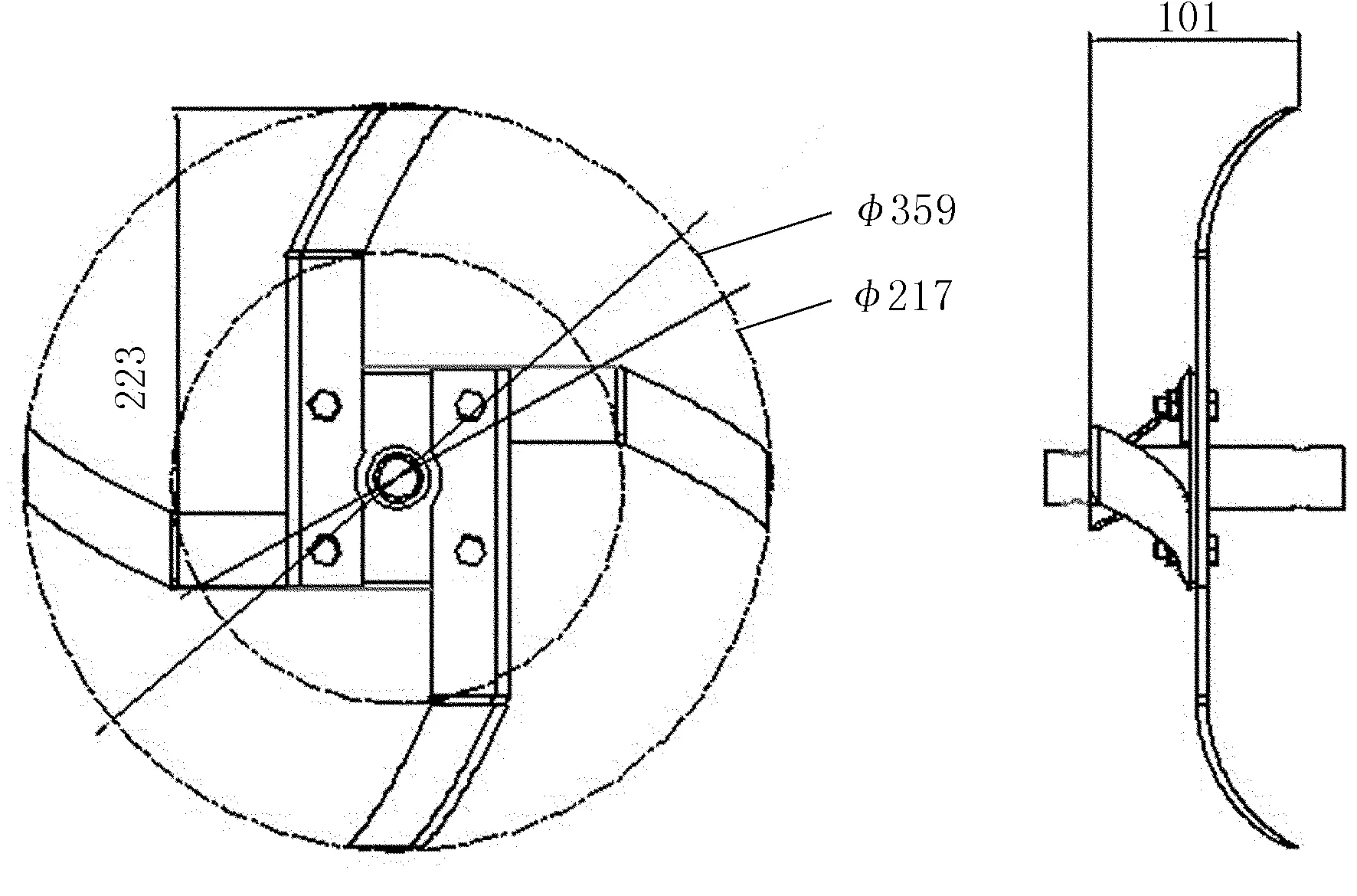
图2 耕刀模型Fig.2 The tillage blade model

2 土壤离散元模型的理论基础

Hertz-Mindin with JKR(Johnson-Kendall-Roberts)Cohesion是一个凝聚力接触模型，可以考虑在接触区域中范德华力的影响和允许用户模拟强粘性的系统[11]，如干燥分粉末、粘结力强的粉体和颗粒。这个模型里，法向弹性接触力实现基于JKR理论。

2.1 土壤之间的接触力学模型

在运动过程中每个颗粒都是相互独立的，只有当发生接触时才会在接触点处产生相互作用，土壤在相互作用时产生的是弹性接触模型，应用Hertz接触模型，示意图如图3所示。其中，R1和R2分别为土壤粒子半径；Z1和Z2为接触半径；A为接触圆半径；δ为接触变形量。其可以拆分成法向振动模型、切向振动运动模型和滑动模型，如图4所示。[12]。

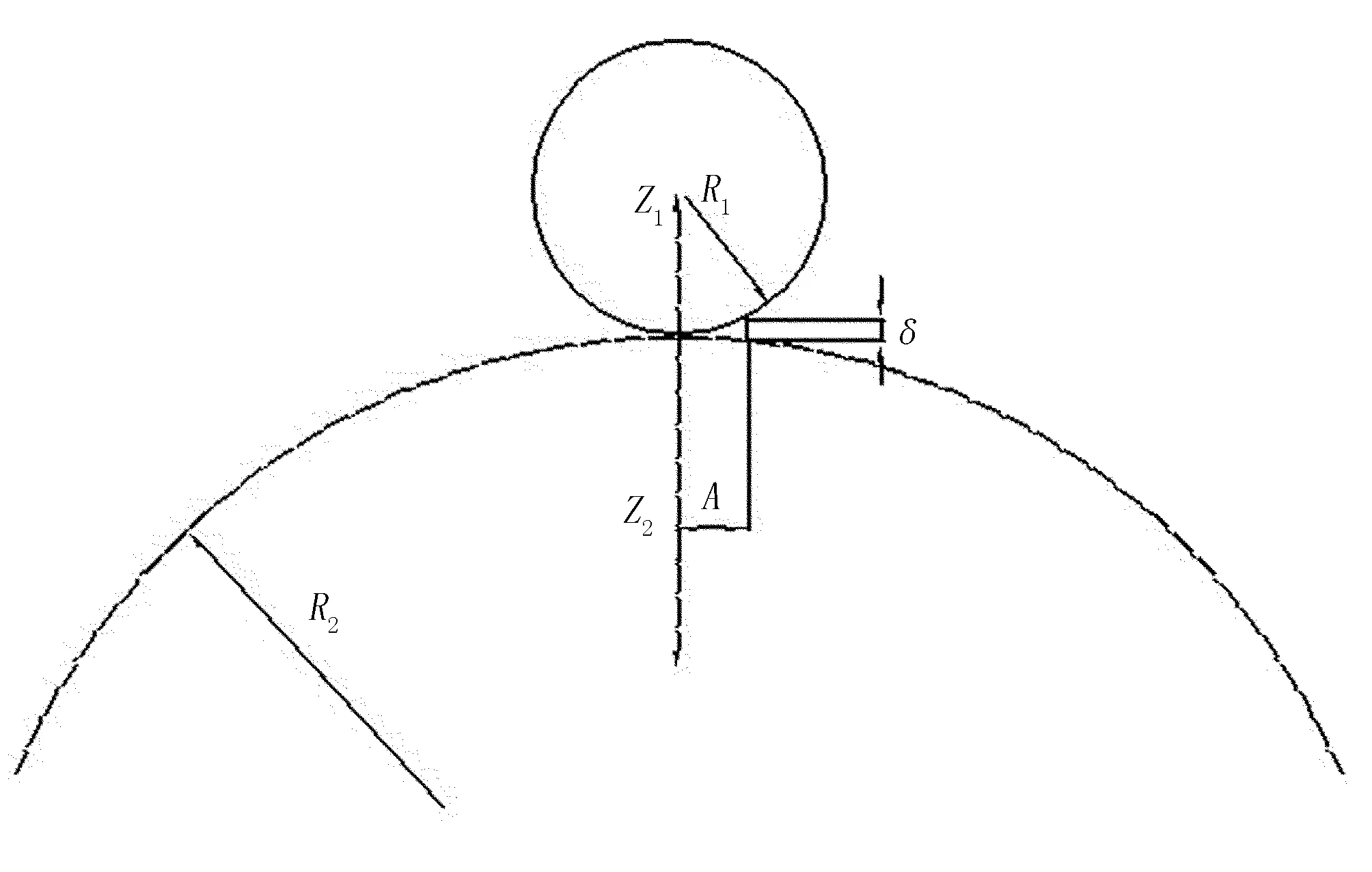
图3 Hertz接触模型Fig.3 Hertz contact model

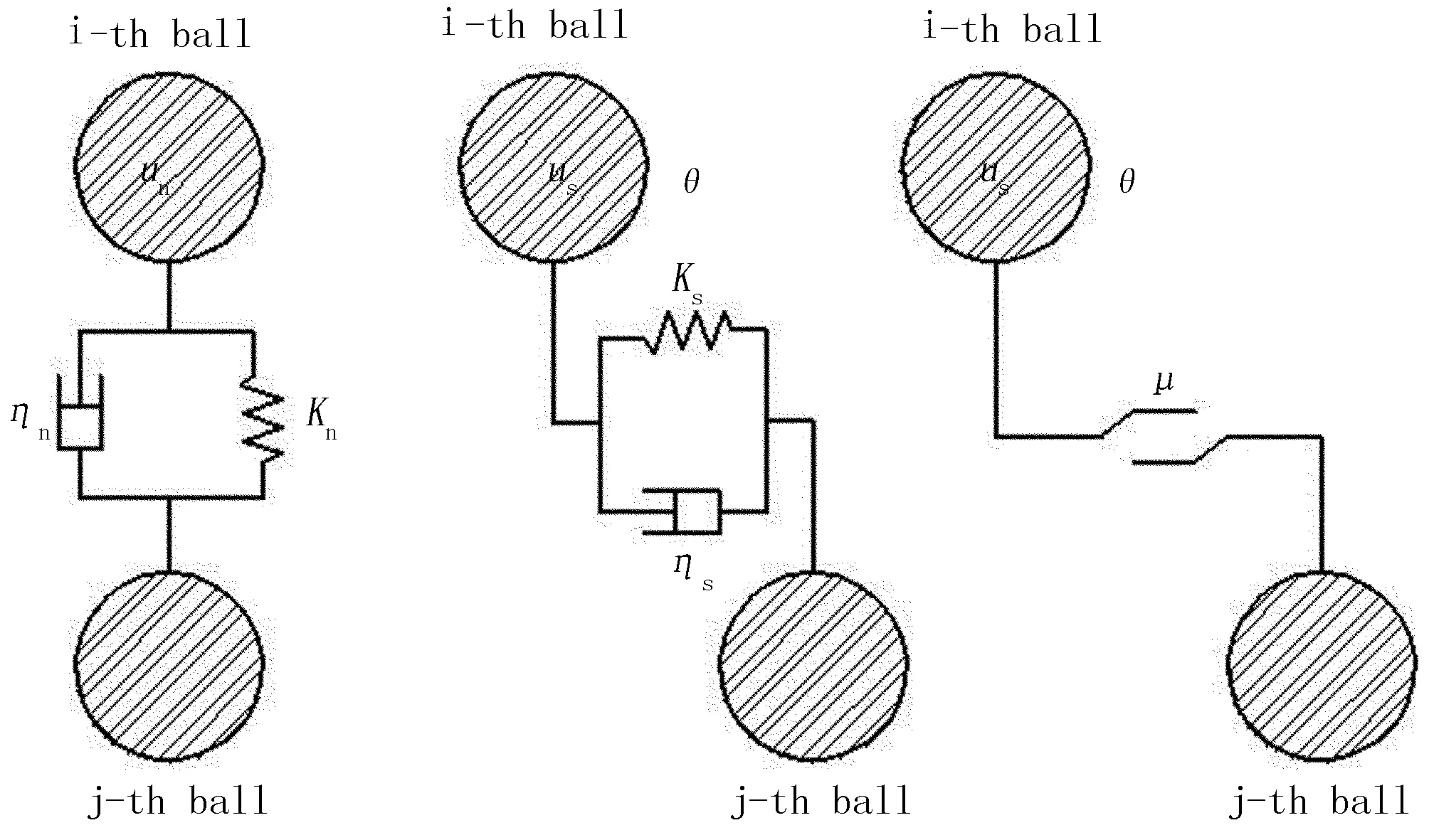
图4 法向振动模型、切向振动运动模型和滑动模型Fig.4 Normal vibration model、Tangential vibration model and slide-model

2.2 土壤模型的参数计算方法

将颗粒接触过程的振动运动进行法向和切向分解，其法向接触力为

式中kn—法向刚度；

E*—当量杨氏模量。

接触时的切向力为

式中δτ—切向重叠量；

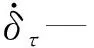
μ—滑动摩擦因数；

Sτ—切向刚度。

3 不同土质下土壤切割状况分析

3.1 建立离散元模型

通过EDEM软件建立单组耕刀与土壤的离散元模型，并对耕作效果进行分析。将耕刀的三维模型另存为X-T格式文件，导入到EDEM中，土壤颗粒之间的算法设置为Hertz-Mindin with JKR ；设置重力方向、土壤参数和材料参数并输入到程序中；创建颗粒工厂几何模型，最大安置颗粒次数为20。耕刀刚刚切入土壤时刻的耕作情况如图5所示。

农机管理部门在做好农业机械设备推广、农机技术推广培训的同时，还要协调和督促相关农机生产企业做好产品三包和售后服务工作。农机手在开展农业作业之前，一定要进行岗前培训，并严密监测培训过程中农民群众农机驾驶问题，做好用户后期回访，不断增强农机手的操作水平和操作质量[3]。

图5 耕刀耕作情况Fig.5 The cultivation of the tillage blade

在使用Hertz-Mindin with JKR模型时，土壤粘结键最大受力由粘结键能量所决定，而旋耕刀具的最适耕作土壤的湿度为20%～30%，为探究何种能量下的离散元JKR模型最适宜模拟农耕土壤，分别为模型赋予10、20、30J的粘结键能量，其切割土壤时的土壤颗粒速度矢量图依次如图6、图7、图8所示。

图6～图8分别展示了两个切割瞬间刀具在切割土壤时土壤颗粒的运动情况和粘结键情况。图中，土壤颗粒不再是以小颗粒形式存在，而是以矢量箭头形式表示，矢量方向表示颗粒的运动方向，速度大小用颜色来表示。速度越大颜色越接近于红色，速度越小颜色越接近于蓝色。图中大部分土壤堆积在刀具一侧，矢量箭头呈蓝色，表明其处于静止堆积状态。与蓝色相连紫色表示相邻颗粒的粘结键，当紫色存在时表明土壤呈接触状态。通过观察粘结键的颜色，可以判断土壤颗粒的破碎情况。

图6 粘结能量10J土壤切割情况Fig.6 The soil cutting condition of 10J bonding energy

图7 粘结能量20J土壤切割情况Fig.7 The soil cutting condition of 20J bonding energy

图8 粘结能量30J土壤切割情况Fig.8 The soil cutting condition of 30J bonding energy

分析可知：图6中运动的土壤颗粒较多，粘结键断裂较多，运动的土壤颗粒运动速度维持在0.62m/s附近。由于土壤颗粒随刀具运动情况较好，运动颗粒多，颗粒先随刀具翻入然后随刀具翻出，翻土效果好。图7中颗粒的运动情况较差，刀具只使刀刃和紧邻刀刃前方的部分颗粒运动，刀具附近其他颗粒受到刀具切割力但粘结键并未发生断裂，运动的土壤颗粒速度维持在0.57m/s附近。由于土壤颗粒随刀具运动情况一般，运动颗粒数较少，翻土效果一般。图8中颗粒的运动情况差，刀具只使刀刃前方的颗粒运动，刀具附近其他颗粒受到刀具切割力但粘结键并未发生断裂，运动的土壤颗粒的速度维持在0.49m/s附近。由于土壤颗粒随刀具运动情况差，运动颗粒较少，颗粒先随刀具翻入然后随刀具翻出，翻土效果差。对比耕刀对土壤的破碎情况可知，土壤翻土效果由好到差依次为10、20、30J。

3.2 耕刀受力分析对比

根据在3种能量粘结键下所做的耕刀工作仿真结果，可以得到不同粘结键能量下耕刀的受力曲线与扭矩曲线相似，其值从小到大依次为10、30、20J，如图9、图10所示。

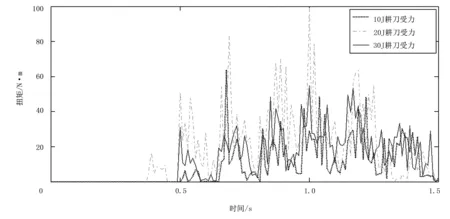
图9 3种能量状态下刀具扭矩输出对比Fig.9 The tool torque output contrast of three kinds energy state

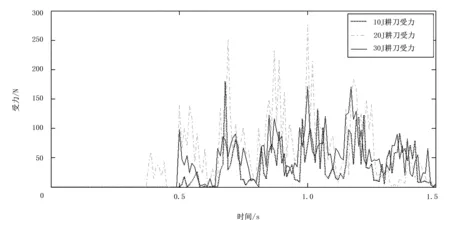
图10 3种能量状态下刀具受力对比Fig.10 The tool force contrast of three kinds energy state

每次耕刀切割土壤会引起耕刀的扭矩或受力增大，当耕刀完成一次切割，耕刀扭矩或受力减小趋近于零，呈现出扭矩或受力曲线的一次起伏。曲线起伏位置相同，说明耕刀在3种能量下前进速度和转速相同。不同粘结键能量下耕刀的受力与耕刀所受的扭矩曲线相似，其从小到大依次为10、30、20J。

根据耕刀对土壤破碎情况时可知：10J和20J时，耕刀对土壤破碎较好，致使土壤的粘结键断裂较多。因此，当粘结键能量越大(20J)时，扭矩和受力值越大；而当土壤粘结键能量过大(30J)时，土壤呈现泥状特征，耕刀在切割土壤时只切割耕刀所走路径上的土壤，对土壤的破碎力最小，此时虽然粘结键能量最大，但因其破碎土壤差，破坏粘结键少，所以对耕刀的受力和扭矩并不是最大。耕刀所需的扭矩和受力呈现非线性，即不随土壤的能量增大而增大。

4 不同土壤能量下耕刀的动力学状况

单一DEM法中机械部件被视为面单元，无密度、无质量、转动惯量等物理参数，造成接触失真。为了得到耕刀的精细运动情况，采用EDEM和ADAMS的动力学耦合算法进行研究。在ADAMS中结合使用IF函数和STEP函数，为设备提供控制扭矩的动力源。IF函数做转速限制，STEP函数应用3次多项式的海德塞维阶跃函数对设定转速做逐步数值逼近。当耕刀的转速低于额定转速时，耕刀的扭矩以极大值400N·m为耕刀提速；当耕刀接近额定转速时，耕刀以旋耕机设计额定转矩50N·m，对耕刀进行提速，达到额定转速573(°)/s时，动力输出消失，从而取得模拟耕刀的动力源。

对土壤粘结键分别为10、20、30J时的耕刀耕作情况进行仿真，分别得到耕刀的角速度、角加速度和扭矩输出曲线，如图11所示。

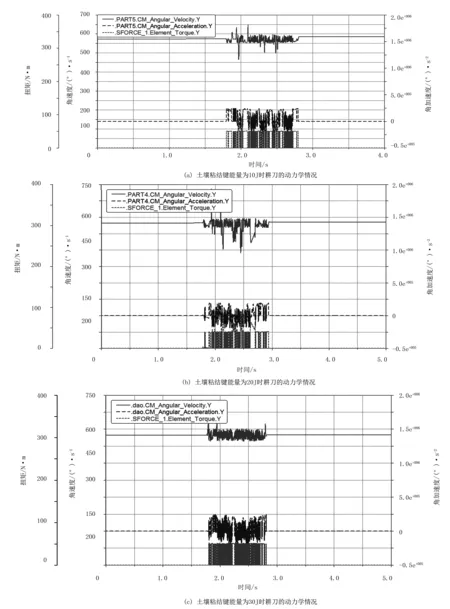
图11 不同土壤粘结键下耕刀的动力学情况Fig.11 The dynamics of the tillage blade under different soil bond energy

由图11可知：运动初始阶段，耕刀速度保持在573(°)/s，转速、角速度、扭矩输出都为零。约1.8s左右，耕刀与土壤接触，对耕刀造成反向阻力，由于外界的应激反力使耕刀减速，动力源函数在发现耕刀转速低于额定转速时为耕刀提供正向扭矩，进而角加速度也发生变化。同时，外界应激反力越大，刀具的减速越快，动力源提供的扭矩越大，角加速度波动越大，以迫使耕刀角速度保持在573(°)/s附近。约2.9s时，激振力消失后角速度恢复573(°)/s，耕作结束。

将3种土壤情况下的3种曲线分别提出，并整合在一起进行对比，如图12所示。

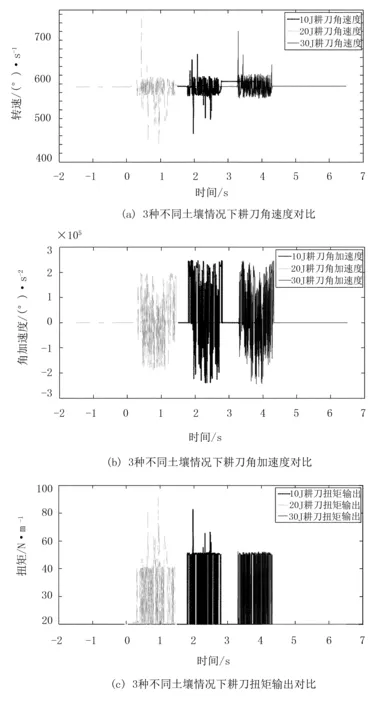
图12 3种不同土壤情况下耕刀动力学曲线对比Fig.12 The dynamics comparison of the tillage in three different soils

由图12可知：在3种不同土壤粘结键能量下，耕刀角速度由小到大依次为20、10、30J，角速度稳定性则恰恰相反。依据3种不同土壤情况下耕刀角加速度和耕刀扭矩输出对比曲线图，土壤粘结键能量为20J时土壤的角加速度值波动最小，当土壤粘结键能量为30J时有所增大，土壤粘结键能量为10J时再次增大，三者呈依次增大规律。角加速度的宏观意义为在动力源和外界应激反力的共同作用下耕刀的角速度变化率的问题。虽然20J时耕刀角速度值波动剧烈，但由于其扭矩输出值为43N·m，扭矩输出变化明显，当遇到激振反力时，保证了角速度变化率较小，但其角速度值变化则剧烈；而10J和30J时，耕刀的扭矩输出为52N·m，扭矩输出平稳。因此，当遇到激振力时，其角加速度变化较为激烈，而速度变化平稳。

分析造成以上现象的主要原因：粘结键能量越大，模拟耕刀破坏土壤时所受的力越大；随着受力变大，耕刀所受冲击变大，表现为耕刀角速度稳定性变差，此时土壤表现为颗粒和块状颗粒群混合状态；当土当能量过大时，土壤颗粒黏成为一个整体，土壤处于泥状，此时虽然刀具克服土壤所需的力变大，但稳定性增强，不产生角速度的突变。

5 结论

1)建立了单组刀具的机械模型，并应用Hertz模型创建了耕刀切割土壤的离散元模型。

2)根据不同粘结键能量，设置3种不同性质的土壤颗粒，并进行了三维耕刀的耕作的仿真。通过观察切割土壤效果和对粘结键破坏情况等因素，确定了当JKR模型的粘结键为10J左右，并得出了不同土质下的耕刀的扭矩与受力动力学曲线，对比分析了动力学特性。

3)不同土壤材质下，刀具的动力学因素与土壤的粘结键能量有关。总体来说，粘结键能量越大，刀具扭矩输出越大，刀具的角速度振动稳定性并不存在正比关系。