遥感卫星载荷海洋耀斑观测几何模型研究

代海山 汪少林 姜通 杨勇 何军 赵其昌



遥感卫星载荷海洋耀斑观测几何模型研究

代海山 汪少林 姜通 杨勇 何军 赵其昌

（上海卫星工程研究所，上海 200240）

为研究遥感卫星观测海洋耀斑时耀斑观测角度及耀斑长度的变化规律，为遥感载荷视场设计提供基础参考数据，文章在假设海洋表面完全反射的基础上，建立了卫星载荷海洋耀斑观测的完全几何模型，确定了卫星观测海洋耀斑的镜面反射极限位置，并建立方程组求取耀斑观测边缘视场指向角，以此获取耀斑观测角和耀斑长度。结合轨道仿真软件（Satellite Tools Kit，STK），以夏至日和冬至日的太阳同步轨道为算例，完成边缘视场耀斑观测指向角、耀斑观测角、耀斑长度的计算。结果表明，耀斑观测参数呈现明显的轨道周期特性，两个耀斑观测边缘指向角在冬至日和夏至日变化趋势相似，但变化范围不同；耀斑观测角呈类正弦变化，最大约为0.43°；耀斑长度夏至日时在0~29.2km范围内变化，冬至日时在0~29.7km范围内变化。通过STK软件生成的耀斑观测指向角与文章模型生成的耀斑观测边缘视场指向角进行对比验证，表明耀斑观测几何模型正确、合理，可为卫星遥感载荷的海洋耀斑观测或规避提供理论依据和边界条件。

遥感载荷视场设计 海洋耀斑 观测几何模型 仿真分析 “高分五号”卫星

0 引言

海洋耀斑（Sun glint）是指太阳光入射到海洋或内陆水体上所形成的一种镜面反射现象。通过分析和处理MODIS、MERIS及卫星SAR在海洋耀斑区域的卫星数据，可实现对海洋溢油的遥感监测[1-3]，而实现对海洋水色及海藻天基观测，需去除耀斑对海藻反演的影响[4-5]。通过建立海洋耀斑反射模型[6]，也可实现对海面波高和海洋水色的探测[7]，进而可反演获取海面风场[8]。遥感卫星通过耀斑对海洋区域进行观测已发展成为海洋遥感的一种重要手段[9]。因此，遥感卫星在观测海洋区域时，遥感载荷的海洋耀斑观测几何参数确定就显得尤为重要。卫星观测海洋耀斑区域时，载荷观测到的耀斑区域的反射率和辐亮度急剧增加[10]，通常会对卫星正常观测任务产生影响，尤其针对高光谱载荷，需充分分析海洋耀斑观测视场，对耀斑成像区域的数据进行耀斑观测几何和辐射传输建模[6,11]，并对耀斑成像区域数据进行特殊处理[12]；对于主动激光雷达载荷，需要通过确定耀斑成像的视场及几何信息，对仪器视场进行优化以规避海洋耀斑区域；针对特殊的观测任务，如“高分五号”卫星的大气环境探测任务，针对海洋区域的温室气体（CO2、CH4等）探测[13]，需设计特殊的耀斑跟踪观测模式[14]，获取海洋上空高信噪比的观测数据[15-17]。由于诸多轨道仿真方法或仿真软件（Satellite Tools Kit，STK）仅能实现对耀斑中心观测指向角的仿真[18-19]，无法获取耀斑观测角以及可观测的耀斑大小信息，因此需发展一种简单有效的仿真计算耀斑观测角度及大小（本文中为可观测到的耀斑长度）的方法，为载荷视场设计提供理论依据。

本文基于海洋镜面反射原理，建立卫星载荷耀斑观测几何模型，确定了卫星可观测到海洋耀斑的极限视场位置，依据两个极限位置确定了耀斑的观测视场角，分析了耀斑观测视场角与可观测到的耀斑长度随卫星轨道位置的变化规律，为卫星载荷的耀斑观测或规避提供边界约束条件。在卫星载荷视场设计过程中，可依据该模型提供的耀斑观测指向角和耀斑观测角，确定观测耀斑指向的角度范围及耀斑指向跟踪的精度；若为规避海洋耀斑，也可根据计算可观测的耀斑角度范围及指向范围进行载荷视场规避设计，为载荷视场设计提供边界条件；在卫星入轨后也可依据计算耀斑观测的角度范围确定卫星观测数据中耀斑观测数据，为后续相应的耀斑观测数据预处理提供基本的几何观测信息[20]。

1 耀斑观测几何模型

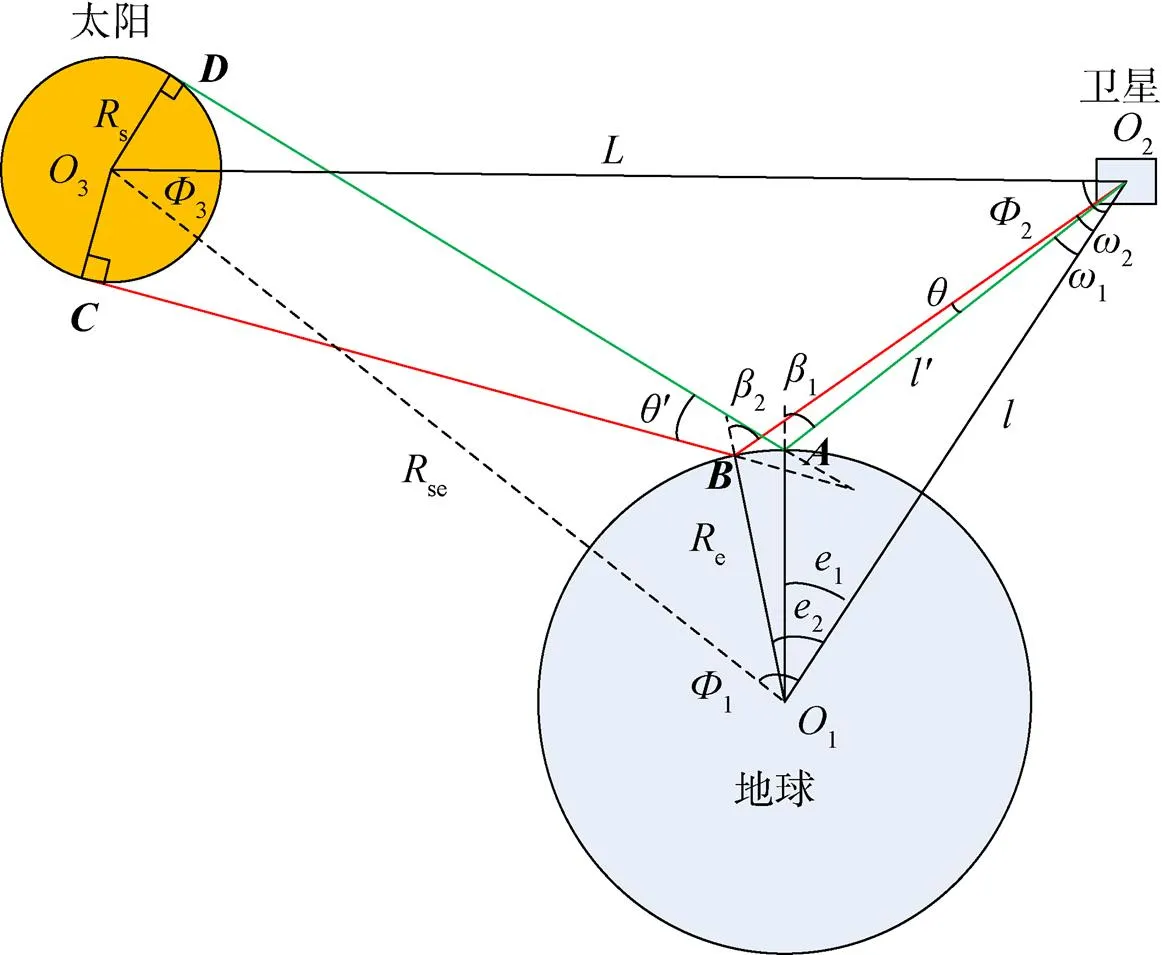
图1 海洋耀斑观测几何模型

根据几何关系，可形成以下方程：

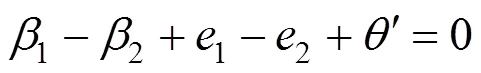
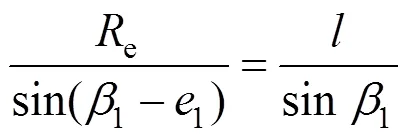
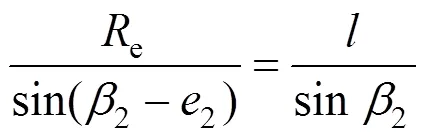
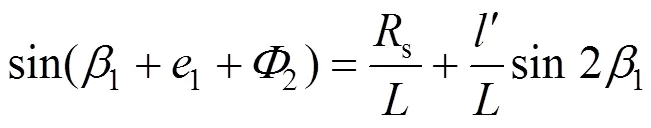
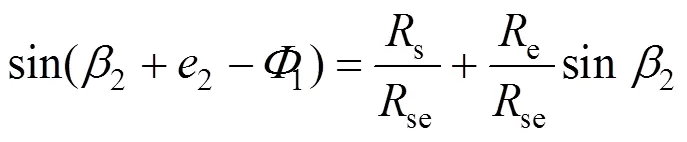
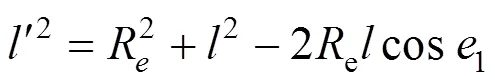
由式（2）、（3）可得到如下关系式

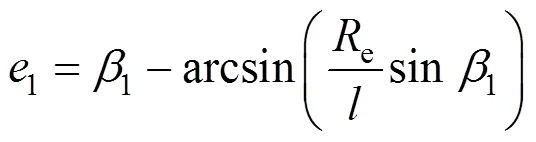
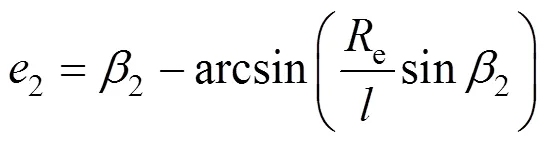
将式（6）、（7）、（8）带入式（4）、（5）可得如下关系式

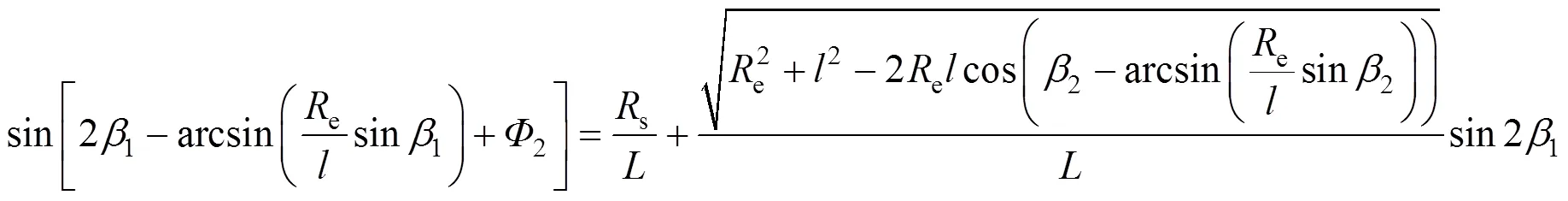
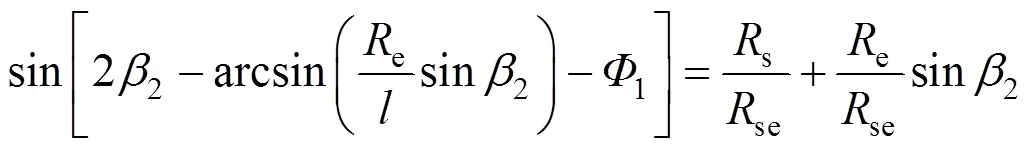
可对式（9）、(10)求1、2的数值解，其中，1与2需满足以下关系式

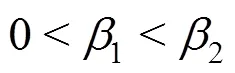
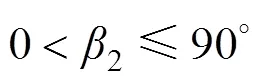
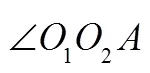
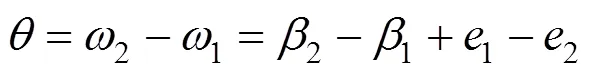
此时，可观测到的耀斑长度可表达为

= πe(2–1)/180 （14）

2 耀斑计算流程

海洋耀斑观测参数的计算流程如图2所示。

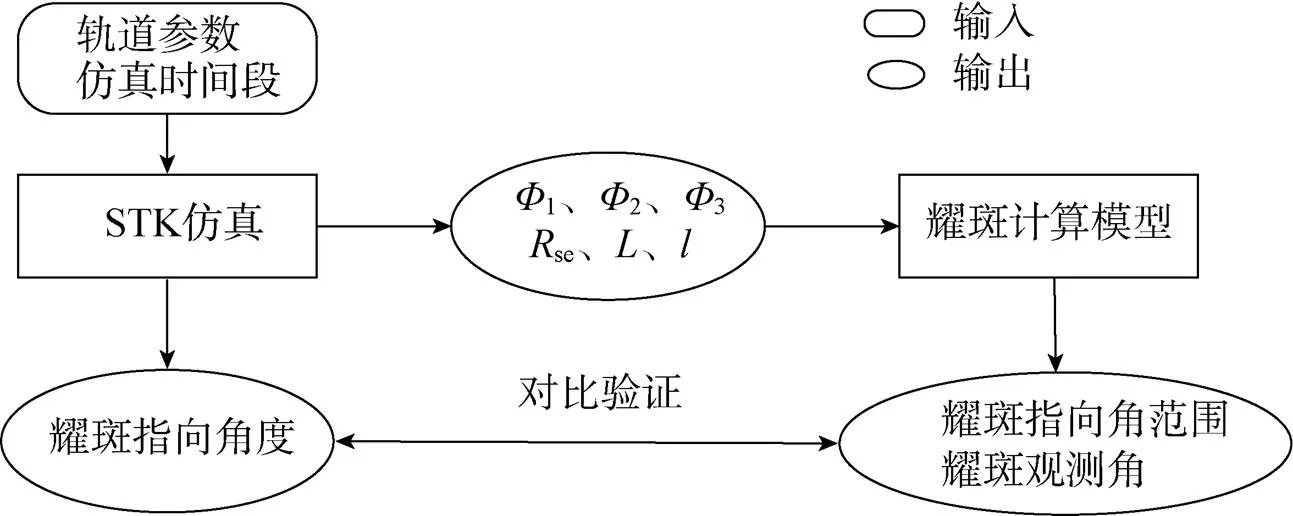
图2 耀斑计算流程图

1）输入轨道参数及仿真计算时间段到STK软件中，输出在耀斑计算中的太阳、地球、卫星三体之间的关键参数：1，2，3，se，，；利用STK中仿真的功能，输出卫星与海洋耀斑的中心点的矢量与卫星轴之间的夹角，也即耀斑指向角。

2）将计算获得的1、2、3、se、、输入到耀斑计算模型中，计算可观测到耀斑的耀斑指向角范围与耀斑观测角。

3）将STK仿真获得的耀斑指向角与耀斑计算模型获得耀斑指向角进行对比验证，验证计算的准确性。

为了验证耀斑计算模型的准确性，使用STK软件首先建立卫星中心位置点与耀斑位置点(Sunglint Point)的矢量，计算该矢量与星下点矢量之间的夹角，记录该角度为stk。按照理论模型，若2–stk>0，1–stk<0，则表明计算结果正确。

3 计算分析结果

选取高度705km，升交点地方时为13：30，轨道倾角98.2°的太阳同步轨道进行计算。分别对夏至日（2015年6月21日0时0分~2015年6月22日0时0分）和冬至日（2015年10月22日0时0分~2015年10月23日0时0分）的耀斑观测进行计算。计算时每分钟一个点，一天共计1 441个点。

图3为载荷可观测到的耀斑视场角在夏至日和冬至日的变化范围与趋势，其中在耀斑观测角的最大值约为0.43°，变化趋势呈类正弦变化。依据方程（13），为2与1角的差值；1与2角变化趋势如图4所示，夏至日和冬至日时，1和2的变化趋势相似，但变化范围不同，如表1所示。图5为耀斑的镜面反射角1与2的在夏至日和冬至日的变化曲线，当1与2都为90°时，载荷观测不到耀斑，对应角为0的时刻。图6计算了载荷可观测的耀斑的大小，在夏至日时可观测到的耀斑长度在0~29.2km之间变化，在冬至日时在0~29.7km之间变化。

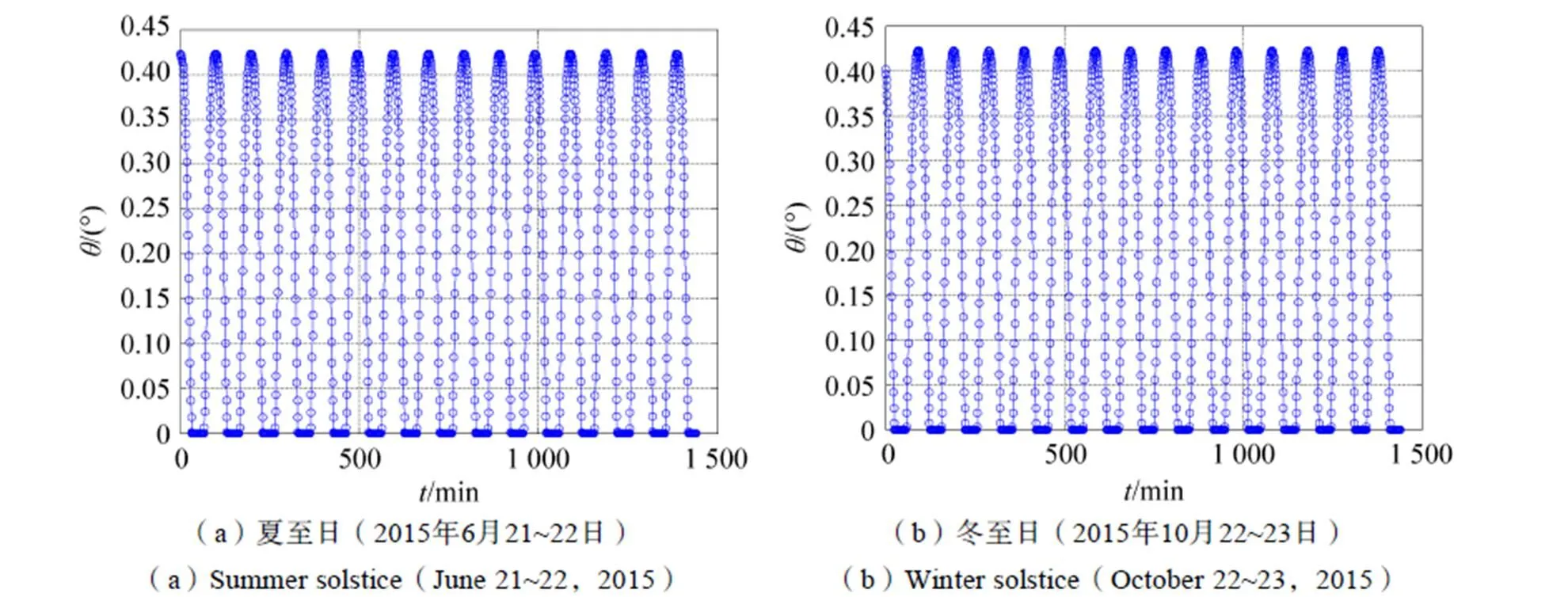
图3 海洋耀斑观测角θ的变化

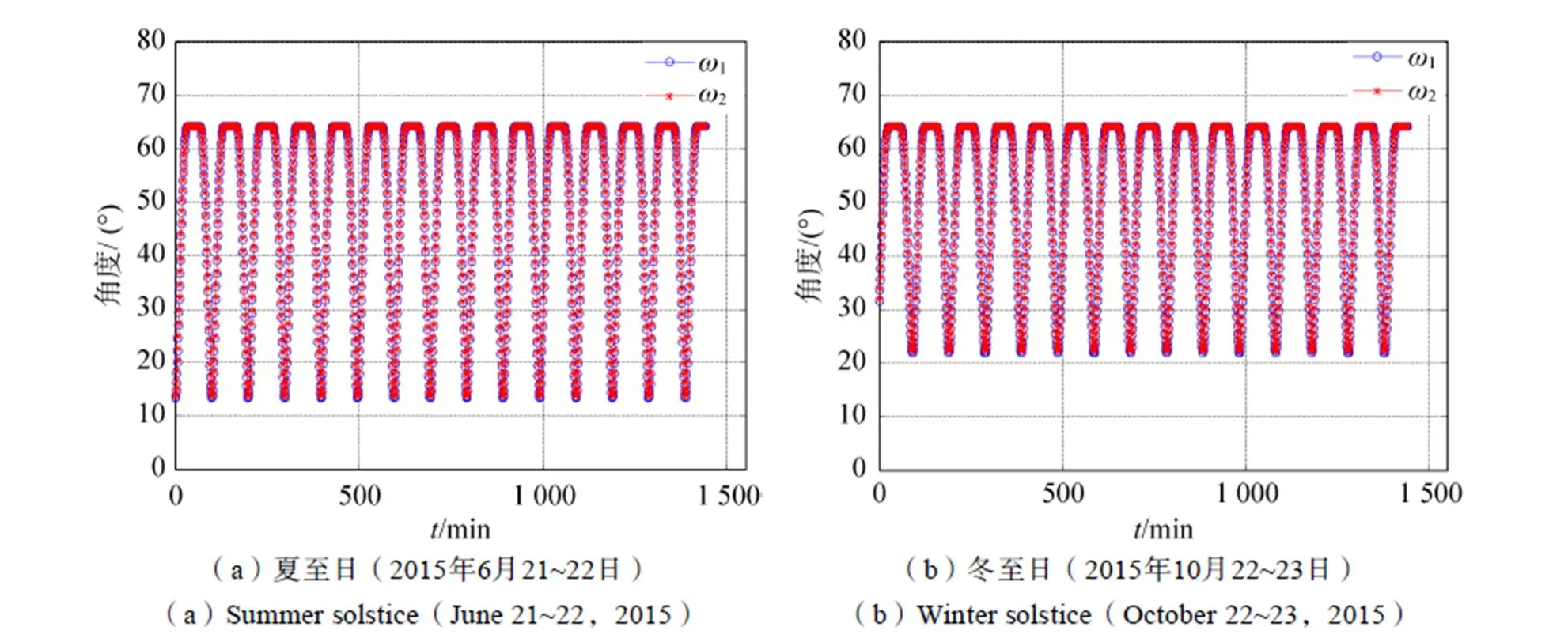
图4 耀斑观测的极限位置视线与星下点视线夹角ω1，ω2的变化

表11和2在不同时间的变化范围

Tab.1 The variation ranges of ω1 and ω2 at summer solstice and winter solstice

为了验证耀斑观测角度计算的正确性，使用STK软件生成耀斑指向角stk与耀斑镜面反射角stk，分别定义为STK中耀斑观测矢量与星下点位置的夹角和在镜面的反射角。利用STK的模拟结果与耀斑模型的计算结果变化趋势基本一致，如图7所示。由于stk与1和2的差值很小，因此进行作差比较。从图8中可以看到，作差分析发现在镜面反射角接近90°的临界区域存在数据的突变问题，分析这一现象的发生主要原因是当2和stk达到90°时，模型计算的2和stk为0，而同一时间点的1还未达到90°，此时stk为临界处的值（约62°）。当两组数据进行作差时就会发生这种现象。此外在作差分析发现在镜面反射角接近90°的临界区域存在1–stk>0的情况。由于STK软件计算的stk考虑了更加精细的模型，如地球的非球形模型，而在耀斑计算模型中认为地球是球形的，这一原因造成了耀斑在镜面反射角接近90°的临界区域发生数据不符的情况。但可以看到，这一偏差非常小，且在其他大部分时间内，数据验证的结果都符合要求，故在本文耀斑计算的几何模型中可忽略这一偏差。

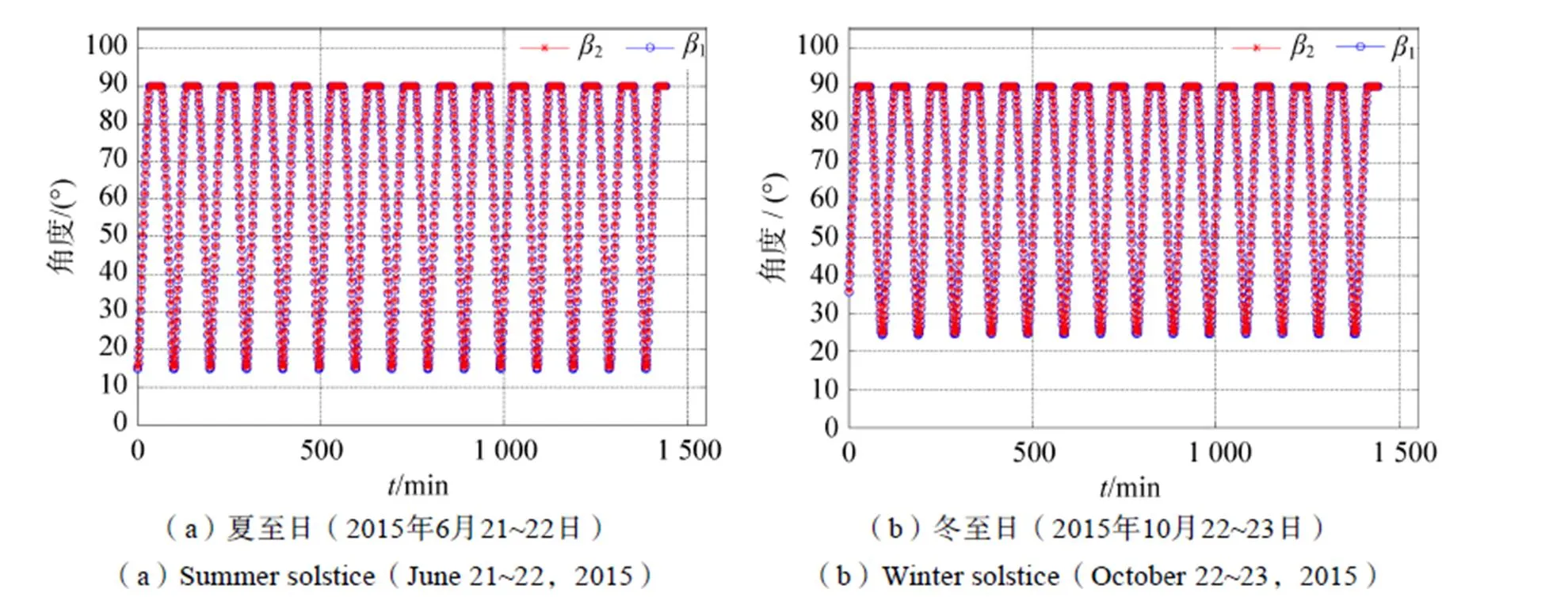
图5 耀斑镜面反射角β1，β2的变化

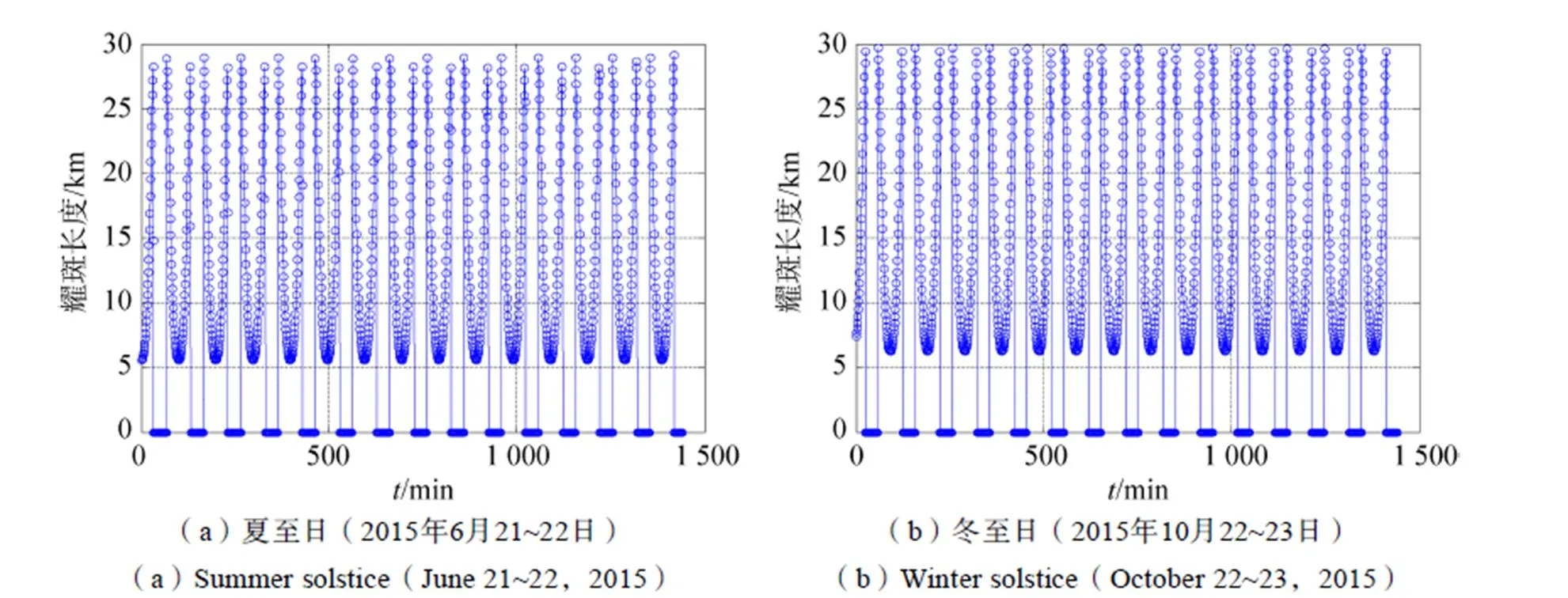
图6 可观测到的耀斑长度的变化

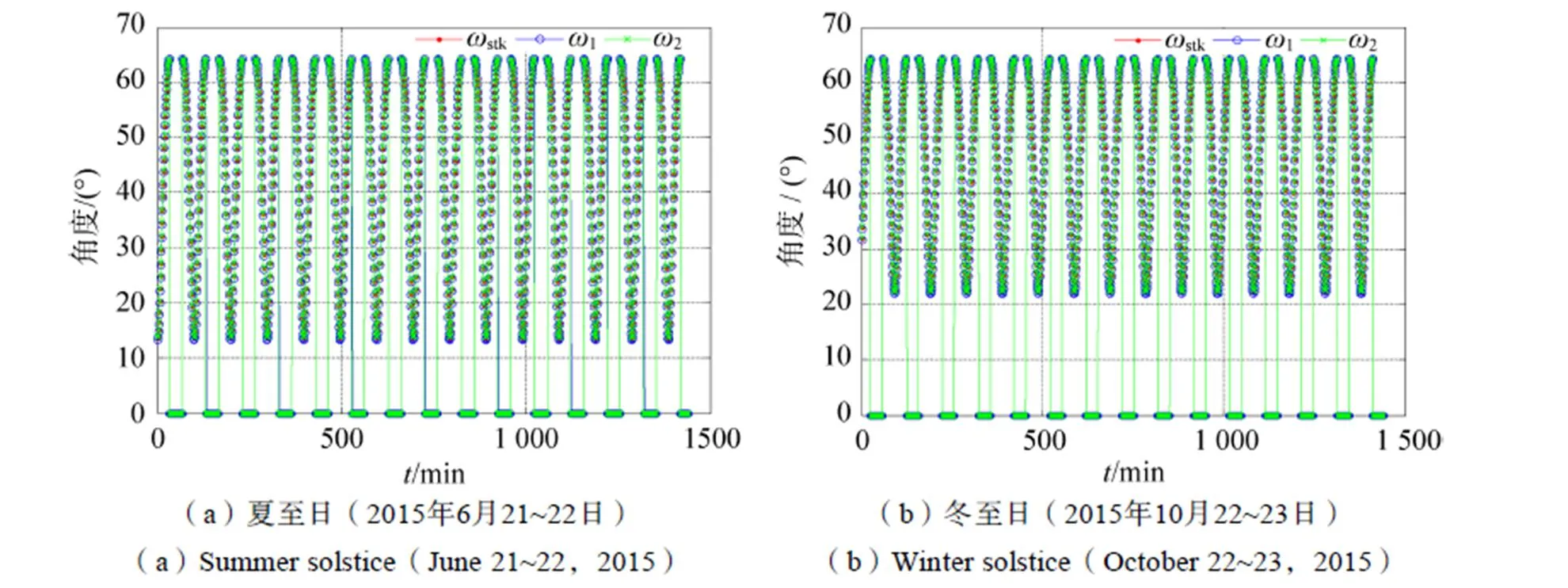
图7 ωstk，ω1，ω2的变化

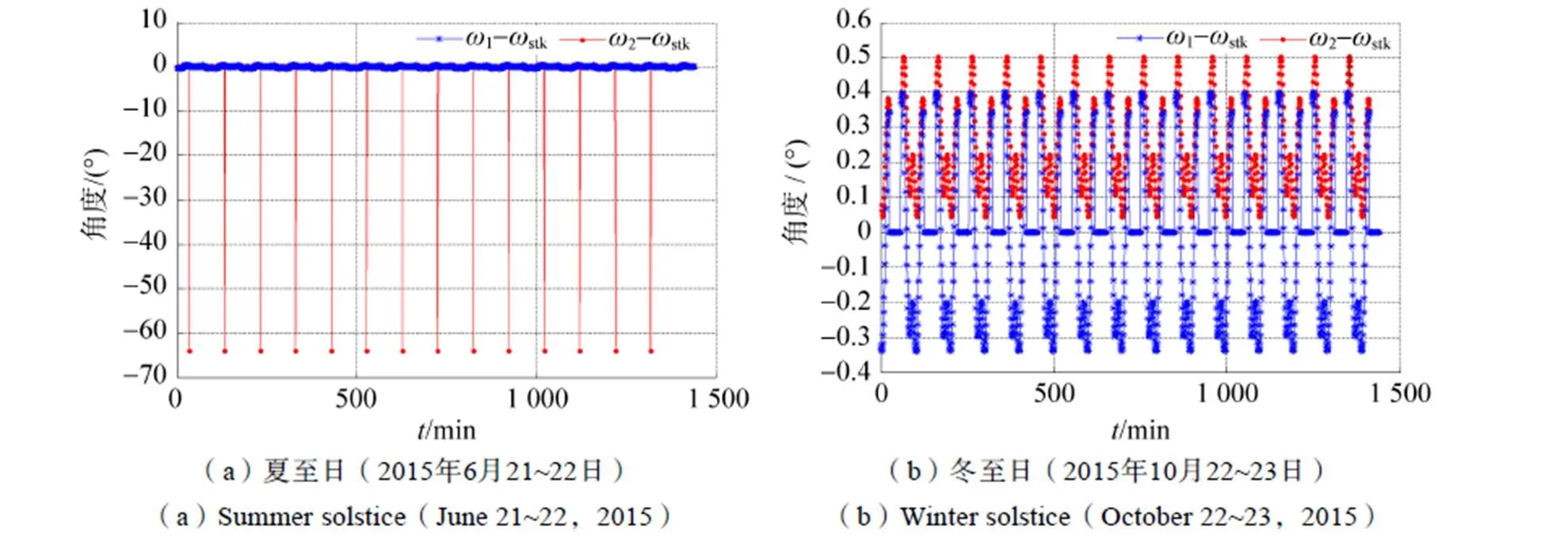
图8 ω2–ωstk，ω1–ωstk变化

为了分析载荷在一轨内耀斑计算模型的计算结果与变化趋势，对2015年6月21日0点0分至1点40分和10月22日0点0分至1点40分两段时间，各100min的耀斑观测进行精细计算，每2s计算一组数据，结果如图9和图10所示，各参量的变化趋势与长时间的计算结果一致；由于计算的时间间隔缩短，故各曲线变化更加平滑和连续。

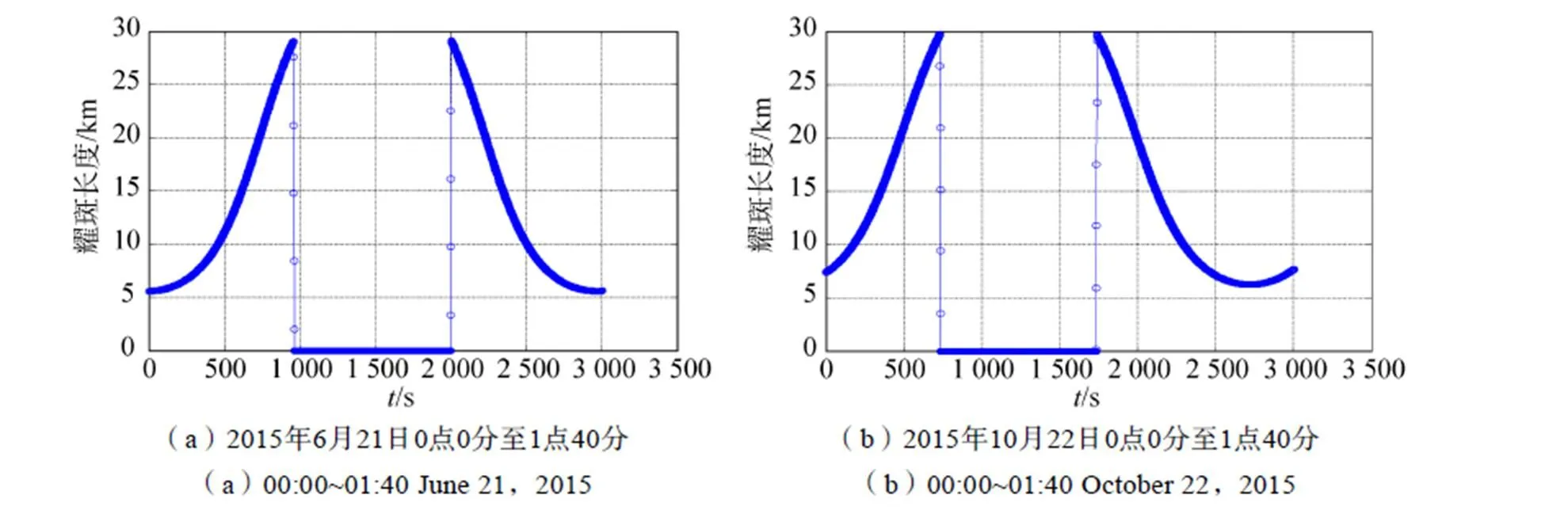
图10 耀斑长度在一轨内的变化

4 结论

本文建立了卫星遥感海洋耀斑观测通用几何模型，计算了太阳同步轨道卫星遥感载荷在轨观测时耀斑的观测角及大小，通过分析夏至日和冬至日的耀斑观测数据，可得到以下结论：

1）计算结果显示，海洋耀斑观测角、耀斑的镜面反射角、耀斑长度随轨道的变化表现出一致的周期性。对夏至日和冬至日两天的计算结果由于轨道参数及太阳位置的变化，略有不同，但数据表现出一致的规律性。

2）在高度为705km的太阳同步轨道上，使用本文的耀斑观测几何模型，耀斑观测角度最大为0.43°，耀斑长度最大为29.7km，并随轨道呈现出类正弦变化规律。

3）使用STK生成模拟耀斑观测角对计算结果进行验证。结果表明使用本文的耀斑观测几何模型计算的耀斑观测角合理有效。

本文的研究结果可为耀斑观测和规避提供理论依据，为遥感卫星的载荷总体设计提供参考数据。

[1] CAROLIS G D, ADAMO M, PASQUARIELLO G. On the Estimation of Thickness of Marine Oil Slicks From Sun-Glittered, Near-Infrared MERIS and MODIS Imagery: The Lebanon Oil Spill Case Study[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 559-573.

[2] ADAMO M, CAROLIS G D, PASQUALE V D, et al. Combined Use of SAR and Modis Imagery to Detect Marine Oil Spills[J]. Proc. of SPIE, SAR Image Analysis, Modeling, and Techniques VII, 2005, 5980: 59800I-1-12.

[3] ADAMO M, CAROLIS G D, PASQUALE V D, et al. On the Combined Use of Sun Glint Modis and Meris Signatures and SAR Data to Detect Oil Slicks[J]. Proc. of SPIE, Remote Sensing of the Ocean, Sea Ice, and Large Water Regions, 2006, 6360: 63600G-1-9.

[4] KIM A M, OLSEN R C, LEE K, et al. Using Panchromatic Imagery In Place of Multispectral Imagery for Kelp Detection in Water[J]. Proc. of SPIE, Ocean Sensing and Monitoring II, 2010, 7678: 767807-1-11.

[5] HU Chuanmin. Observing MODIS Ocean Color Patterns Under Severe Sun Glint[J]. Proc. of SPIE, Ocean Sensing and Monitoring III, 2011, 8030: 80300M-1-6.

[6] 李旭光. 海洋内波可见光光学反射特性研究[J]. 舰船电子工程, 2012, 32(11): 131-146. LI Xuguang. Research of Ocean Internal Waves of Visible Light Optical Reflectance Characteristics[J]. Ship Electronic Engineering, 2012, 32(11): 131-146. (in Chinese)

[7] CURETON G P. Retrieval of Higher Order Ocean Wave Spectra from Sunglint[J]. Geoscience & Remote Sensing Symposium, 2010, 53(1): 272-275.

[8] CURETON G P, ANDERSON S J, LYNCH M J, et al. Retrieval of Wind Wave Elevation Spectra From Sunglint Data[J]. IEEE Transactions on Geoscience & Remote Sensing Symposium, 2007, 45(9): 2829-2836.

[9] MYASOEDOV A, JOHANNESSEN J A, KUDRYAVTSEV V et al. Sun Glitter as a Tool for Monitoring the Ocean from Space[C]//International Conference on Remote Sensing, Nanjing, 2012: 1-4.

[10] SHIOMI K, YOSHIDA M, SEKIO N. Study for Sun Glint Observation of GOSAT FTS Using MODIS and AMSR-E Data[C]//IEEE International Conference on Geoscience & Remote Sensing Symposium. Denver, 2006: 2060-2063.

[11] 石广玉. 大气辐射学[M]. 北京: 科学出版社, 2007. SHI Guangyu. Atmospheric Radiology[M]. Beijing: Science Press, 2007. (in Chinese)

[12] MILLER C I. Evalution of Sun Glint Correction Algorithms for High-spatial Resoluton Hyperspectral Imagery[D]. California USA: Naval Postgraduate School, 2012.

[13] 孙允珠, 蒋光伟, 李云端, 等. 高光谱观测卫星及应用前景[J]. 上海航天, 2017, 34(3): 1-13. SUN Yunzhu, JIANG Guangwei, LI Yunduan, et al. Hyper-spectral Observation Satellite and It’s Appliacation Prospects[J]. Aerospace Shanghai, 2017, 34(3): 1-13. (in Chinese)

[14] 石广玉, 戴铁, 徐娜. 卫星遥感探测大气CO2浓度研究最新进展[J]. 地球科学进展, 2010, 25(1): 7-13. SHI Guangyu, DAI Tie, XU Na. Latest Progress of the Study of Atmospheric CO2Concentration Retrievals from Satellite[J]. Advances in Earth Sciences, 2010, 25(1): 7-13. (in Chinese)

[15] O′BRIEN D M, POLONSKY I, O'Dell C, et al. Testing the Polarization Model for TANSO-FTS on GOSAT Against Clear-sky Observations of Sun Glint Over the Ocean[J]. IEEE Transactions On Geoscience And Remote Sensing, 2013, 51(12): 5109-5209.

[16] 代海山. 高光谱卫星遥感温室气体二氧化碳反演技术研究[D]. 西安: 西安交通大学, 2012 DAI Haishan. The Inversion Technique of Atmospheric CO2from Satellite-based Hyperspectral Observations[D]. Xi′an: Xi′an Jiaotong University, 2012. (in Chinese)

[17] 吴军, 王先华, 方勇华, 等. 空间外差光谱技术应用于大气二氧化碳探测的能力分析[J]. 光学学报, 2011, 31(1): 1-7. WU Jun, WANG Xianhua, FANG Yonghua, et al. Abilitiy Analysis of Spatial Heterodyne Spectrometer in Atmospheric CO2Detection[J]. Acta Optica Sinica, 2011, 31(1): 1-7. (in Chinese)

[18] 陈希军, 李仁. 基于STK的卫星飞行轨迹仿真技术[J]. 哈尔滨商业大学学报(自然科学版), 2008, 24(3): 339-343 CHEN Xijun, LI Ren. Simulation Technology of Satellite Flight Orbit Based on STK[J]. Journal of Harbin University of Commerce (Natural sciences edition), 2008, 24(3): 339-343. (in Chinese)

[19] RYU D, KIM S W, KIM D W, et al. Integrated Ray Tracing Simulation of Annual Variation of Spectral Bio-signatures from Cloud Free 3D Optical Earth Model[J]. Proc. of SPIE, Instruments, Methods, and Missions for Astrobiology XIII, 2010, 7819 78190E-1-14.

[20] 李恺, 张晗. 康晓军. 关于太阳耀斑观测的地图匹配算法实现[J]. 航天返回与遥感, 2014, 35(6): 58-65. LI Kai, ZHANG Han, KANG Xiaojun. Realization of Map Matching Method for Observation of Solar Flare[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(6): 58-65. (in Chinese)

The Research of Sun Glint Observation Geometry Model for Remote Sensing Satellite

DAI Haishan WANG Shaolin JIANG Tong YANG Yong HE Jun ZHAO Qichang

（Shanghai Institute of Satellite Engineering, Shanghai 200240, China）

In order to research the remote sensing satellite variation law of viewing angles and length for sun glint and supply the basic data for instrument viewing geometry, sun glint observation geometry model for remote sensing satellite was built up and the boundary position of sun glint viewing angles was found based on the assumption of the total mirror reflection on the ocean. Then the equations for the boundary angles of sun glint direction were given and the viewing angles and length of sun glint were obtained. With the aid of satellite orbit simulation software（Satellite Tools Kits, STK）, the boundary angles of sun glint direction, the viewing angles and the length of sun glint were calculated in the condition of sun-synchronous orbit at summer solstice and winter solstice. The results show that these sun glint observation parameters present obvious characteristics of orbital period. The boundary angles of sun glint direction have similar variation trend in the sinusoidal wave with different ranges. The maximum viewing angles of sun glint is 0.43 approximately. The length of viewing sun glint for summer solstice and winter solstice are varying between 0~29.2km and 0~29.7km respectively. By comparison and validation with the STK sun glint calculation results, the sun glint observation geometry model presented in this paper is rational and correct，which can provide the theoretical basis and boundary condition of the sun glint observation or avoidance for remote sensing satellite.

field of view design for remote sensing instrument; sun glint; viewing geometry model; simulation analysis; GF-5 satellite

V474.2

A

1009-8518(2018)03-0085-09

10.3969/j.issn.1009-8518.2018.03.010

代海山，男，1987年生，2012年获西安交通大学光学专业硕士学位，主管设计师。研究方向是遥感载荷总体设计及数据应用。E-mail：dhs1314@126.com。

2018-05-05

国家重大科技专项工程

（编辑：王丽霞）