基于蚁群算法的VRPTW问题优化研究
黄秋彬 贺超

【摘要】针对目前物流配送过程中客户对于送货准时性要求日益提升的问题,对每个客户采用时间窗管理约束,作为NP-Hard问题,启发式算法常被用于解决VRPTW问题。本文选取重庆市某物流企业的配送情况进行实例研究,选取其中具有代表性的16个客户点,并对客户进行时间窗管理约束,同时运用蚁群算法进行路径规划研究,研究表明蚁群算法作为启发式算法中的一种能够有效用于解决VPIPTW问题。
【关键词】物流配送;VRPTW问题;蚁群算法
一、引言
车辆路径问题(VRPTW)是物流配送研究中的核心问题,其中对客户加以时间窗约束的车辆路径问题则被称作带时间窗的车辆路径问题(VRPTW),在竞争愈加激烈的现代物流行业,客户的满意度是每个物流企业都需重视的问题,同时考虑到每个客户适宜收货时间的差异性,对客户进行不同的时间窗约束显然更为符合现实情况,因此VRPTW一直受到广大学者的广泛关注和不断研究。对于VRPTW问题的研究方法总体可分为两类:一类是精确算法、另一类是启发式算法。其中精确算法具有较高的求解精度,但由于其求解难度会随着问题的复杂度的增加而呈现指数型增长,难以保证其求解速度。与精确算法相比较而言,启发式算法能够有效运用于大规模问题的求解,更具有实用性。目前较为常用的启发式算法包括蚁群算法、模拟退火算法、粒子群算法、模拟退火算法等[1],本文选取蚁群算法进行VRPTW问题的优化研究。
二、蚁群算法流程
传统的VRPTW问题指的是在满足客户需求量和时间窗限制的前提下,研究配送成本和惩罚成本总和最小的车辆路径问题。蚁群算法最早的提出是为了应用于旅行商问题(TSP),随着蚁群算法的不断改善及优化,如今蚁群算法已能够较好运用于VRPTW问题的求解。
以下是蚁群算法的基本步骤:
(1)nc←0(其中nc代表迭代次数;各τij以及△τi,j进行初始化;m只蚂蚁被放置于n个顶点上。
(2)将各蚂蚁的初始出发点放置于当前解集之中;每一只蚂蚁k(k=1,2,3,…,m)按照概率pi,jk移至下一个顶点j;将顶点j置于当前解集。 (3)计算各蚂蚁爬行的路径长度Lk(k=1,2,3,…,m);记录当前的最优解。
(4)按照相应的方程对轨道强度进行修改。
(5)对各边弧(i,j),置△τi,j←0,nc←nc+1。
(6)若nc小于原先设定的迭代次数并且没有退化行为(即找到的都是相同的解),则转至步骤(2).
(7)结束算法并输出最优解。
三、实例研究
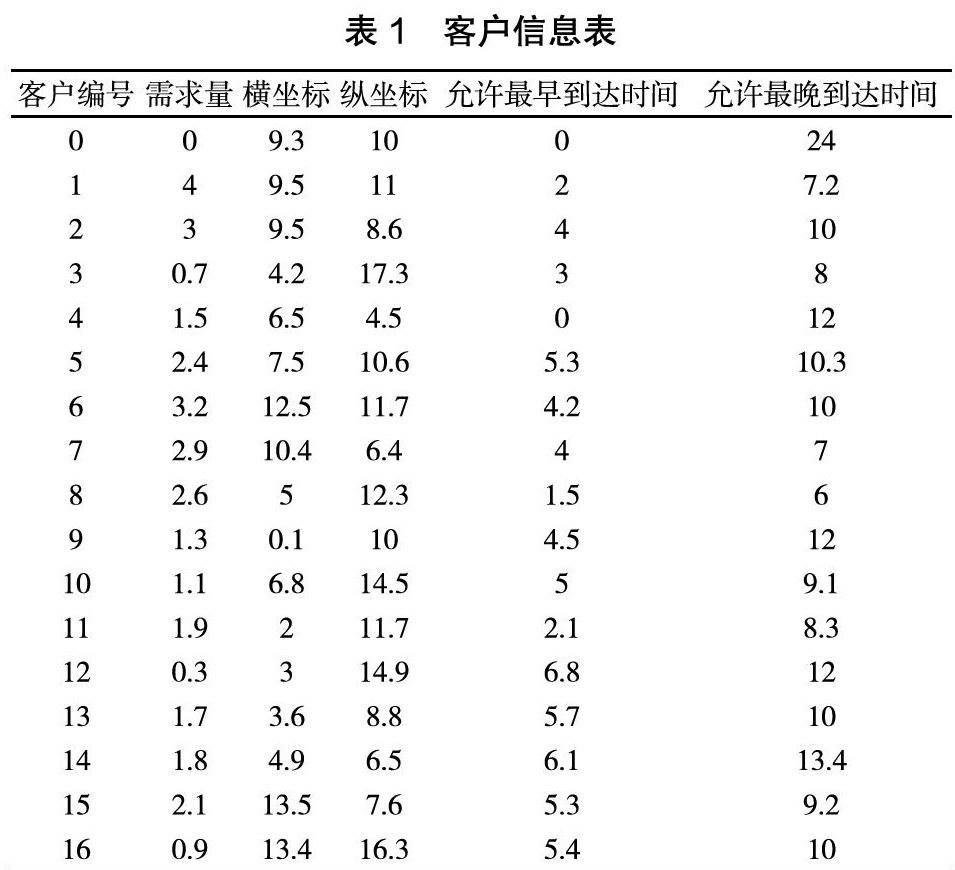
为了验证所提蚁群算法在VRPTW问题中的有效运用性,选取重庆市某物流企业的配送情况进行实例研究,选取其中具有代表性的16个客户点,并对客户进行时间窗管理约束,同時运用蚁群算法进行路径规划研究,相应的客户信息如表1所示:
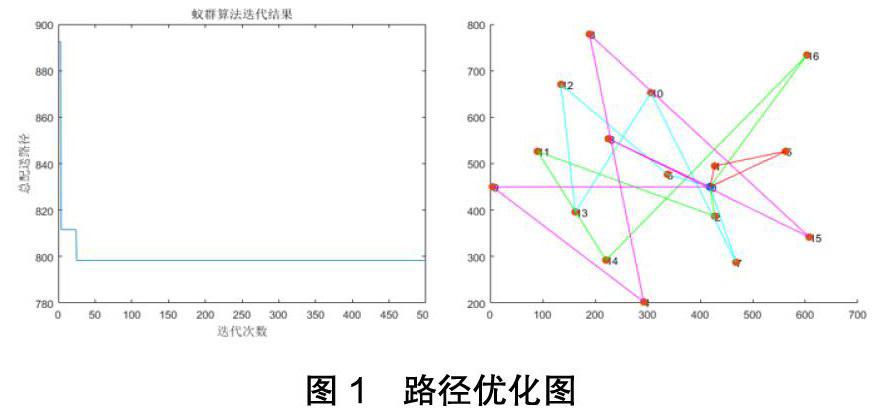
基于表1中的客户信息,采用蚁群算法进行路径优化研究,具体的路径优化结果如图1及表2所示:
四、结论
本文在研究了蚁群算法的基础上,选取重庆市某物流企业作为研究对象,对16个客户进行带时间窗约束下的路径规划研究。MATLAB运行结果显示蚁群算法能够较快收敛,在较短时间内得到最优解,有效证明了蚁群算法在VRPTW问题上的实用性,为相应的研究提供了借鉴思路。
参考文献:
[1]何小锋,马良.带时间窗车辆路径问题的量子蚁群算法[J].系统工程理论与实践,2013,33(5):1255-1261.
[2]唐静.基于蚁群算法车辆路径问题的研究与应用[D].中国科学院大学,2014.
[3]刘志硕,申金升,柴跃廷.基于自适应蚁群算法的车辆路径问题研究[J].控制与决策,2005,20(5):562-566.

