一种基于鲁棒回归的相控阵天线校准技术

四川九洲电器集团有限责任公司 张 抒

1.研究背景

有源相控阵天线具有波束指向捷变，定向增益高等优点，被广泛应用于各领域。但是相控阵天线的副瓣电平、波束指向、波束宽度和零值深度等重要指标会受到诸如移相器误差、制造公差、阻抗不匹配、天线热变形等因素的影响，这些因素最终都反映为各天线通道的馈电幅度和相位的不一致性。因此研究天线校准技术，对提高天线的实际性能至关重要。

常用的校准方法有逆矩阵法、FFT方法、矢量平均法、旋转矢量法等[1][2]。上述方法都是通过改变各通道的移相值来构建方程，并反解出每个通道的幅相值，其共同的缺点是移相器精度对最终的校准精度有较大影响[3]。为了解决该问题，本文提供了一种基于鲁棒回归的天线校准方法，采用稳健线性回归方法拟合样本点，能有效去除样本中的离群点，减弱了移相器误差对校准精度的影响。

2.方法原理

本文方法可应用于有源相控阵天线接收和发射通道远场校准。以接收通道远场校准为例，在接收天线法线方向放置一个信号源，调整各接收通道的移相值，接收合成信号将发生变化，根据信号变化与各通道的相位关系可以反演每个接收通道的校准值。本文方法主要包括样本采集、超平面样本点拟合、超平面参数推导校准值三个步骤。

2.1 样本采集

图1给出了有源相控阵天线接收通道校准框图，包括天线单元、TR组件、和差网络、接收机及信号源，本文方法在该框架下采集数据样本。具体来说，信源产生信号x，由于信源在天线法线方向，则达到天线端口的信号x幅度相位相同。信号经每个天线单元、接收通道和移相器产生不同程度的幅度衰减和相移，设a(i)为第i个通道的幅相偏移，c (i)为第i个通道的移相器值，则第i个通道的输出信号为：

上式均为复信号，●为复数的乘法，s(i)为第i个通道输出信号。校准工作需要估计i通道幅相偏移值a(i)。由于只关心幅相偏移相对值，也可直接估计，因此为了表述方便可用b(i)替代a(i)●

x。信号S(i)送至和差网络，和通道输出为各路信号合成，接收机检测得到和通道信号y。

N为通道数，c (i)为移相器值，y为检测值。通过反复调整移相值c (i)，并记录信号y，获得多组测试数据。记cj(i)为第 j 次调整i路通道的移相值，yj为j次检测值，定义N+1维向量为第j个样本。假设采集了M个样本点，记为。

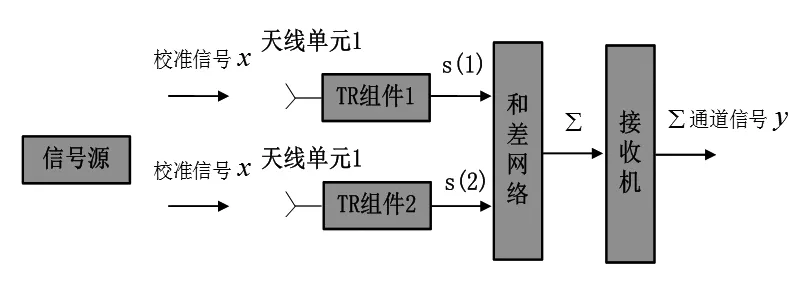
图1 有源相控阵天线接收通道校准框图

2.2 超平面样本点拟合

把c (i)看作自变量，y看作因变量，则式（2）为一个超平面方程，b (i)固定不变为超平面的参数。因此可采用线性回归对样本进行拟合，估计超平面的参数b (i ), i= 1, 2, ..., N。

综合考虑计算效率和拟合精度，本文采用最小二乘法估计超平面参数，其闭式解。当样本数量远大于通道数量时，满足矩阵CTC可逆，可求得的解。

2.3 超平面参数推导校准值

由于每个接收通道的移相器均具有一定移相误差，各通道的误差累计将导致合成信号Y 产生误差，实际的合成信号表示如下：

其中ε为所有通道累计的误差值。直接采用最小均方误差方法拟合样本易受到噪声干扰，鲁棒性较差。本文进一步对拟合得到的参数处理，具体步骤如下：

1）采集L个样本，并满足L＞M，初始化变量k = 0；

2）从L个样本中随机选取M个样本，并满足M＞N，k = k +1；

3）利用最小均方误差方法拟合选取的M个样本，估计第k个粗略超平面参数Bk；

4）判断k ＜ K条件是否满足，如果满足则返回第2步执行，否则执行第5步；

3.仿真结果

仿真实验采用均方根误差衡量幅相校准精度，并比较了几种方法的校准效果。实验设计天线通道数为8，移相器的移相误差服从[—6°—6°]区间的均匀分布，表1给出了1000次蒙特卡洛实验结果。实验表明存在移相误差情况下，本文提出的方法具有更高的校准精度。

表1 几种方法校准精度的比较