地震作用下综合管廊动力特性数值模拟研究

孙先春

(上海市政工程设计研究总院（集团），上海 200092)

关键字：综合管廊；地震作用；动力特性；数值模拟

0 引言

城市地下综合管廊也称为“共同沟”，是在地下建造一个人工空间，将电力、燃气、通讯、市政、给排水等集于一体，实现统一规划、设计、建设和管理[1]。

目前对综合管廊在静力状态下受力和变形机理已作了一些研究。胡翔和薛伟辰[2]通过接头和整体结构足尺模型单调静力试验，对采用预应力筋连接的预制预应力综合管廊受力性能进行了研究，得出综合管廊整体结构的受力过程分为开裂、屈服和极限破坏三个阶段。王灵仙等[3]采用有限元软件对所设计的综合管廊主体结构整体及相关构件进行了受力性能分析，提出增大顶板和框架柱节点处腋板的尺寸以保证管廊的安全性。

全球范围内多次地震震害现象表明，现有地下结构在地震作用下并不安全；日本阪神地震中，地下铁路、停车场、隧道、商业街等地下工程均破坏严重，对未考虑地震因素的地铁站中柱，即使其设计安全系数达到3，地震中仍几乎完全坍塌[4-5]。施有志等[6]对地震作用下综合管廊土-结构接触面参数进行了研究，成果可供地震作用下综合管廊动力响应数值模拟提供参考。杜盼辉[7]利用数值模型分析了综合管廊在横向地震作用下的响应规律，研究了土体加速度的反应规律、土和管廊的相互作用，管廊的位移变化规律。赵丹阳[8]对地震作用下综合管廊交叉节点的动力响应规律进行了研究，分析了交叉节点在地震作用下最危险的部位和环节。然而，目前对地震作用下城市地下综合管廊受力特性的研究还很有限，对地震作用下管廊受力相对于静力状态下的放大系数研究尚未见报道。

本文对某一地下综合管廊建立数值模型，分析其在地震作用下的动力响应和力学特性，并与静力状态下管廊受力特性进行比较，计算结果可供地震作用下综合管廊设计参考。

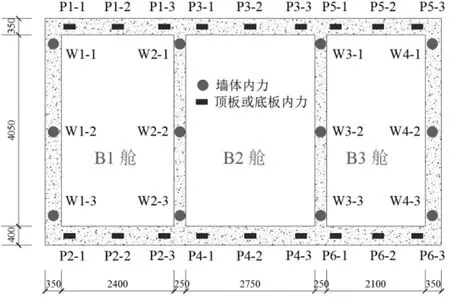
图1 综合管廊三舱标准断面图 （单位：mm）

1 工程概况

图1为某综合管廊三舱标准断面图，净高为4.05 m，左边舱（B1舱）、中舱（B2舱）、右边舱（B3舱）净宽分别为 2.40 m、2.75 m、2.10 m；管廊底板厚度400 mm，顶板和边墙厚度350 mm，中墙250 mm。图中还给出了数值计算过程中管廊墙体、底板以及顶板的内力记录点。

2 数值模型

由于管廊纵向长度要比宽度大很多，地震对宽度方向的影响是主要的，所以采用有限元软件Z_Soil建立平面应变模型研究地震作用下管廊动力特性，如图2所示。

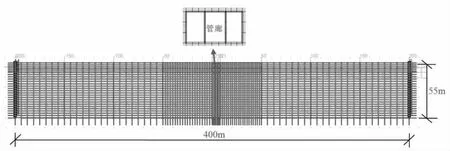
图2 数值模型

数值模型地基土厚度55.0 m，管廊上覆土层厚度5.0 m，水平尺寸为400 m，以降低地震反射波对管廊结构的干扰。管廊墙板采用程序内置的B E AM单元进行模拟，地震波采用K o b e波。地震波往返作用周期约为0.2～1.0 s，即地震作用频率约为1～5 H z[9]，故本文计算过滤了地震波中频率大于5 H z的成分，如图3所示。K o b e波持续时间为25 s，在4.7 s时加速度达到最大，为0.8 g。

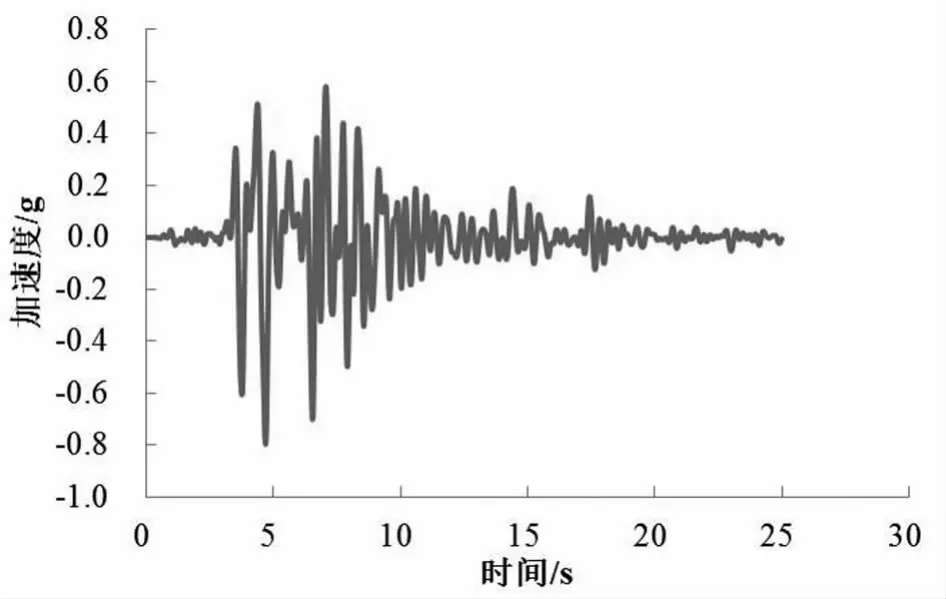
图3 Kobe地震波

地震作用是高速的，会引起地基和结构的小应变变形，其动态刚度要比静态刚度大很多，故管廊墙体采用弹性模型，地基土采用硬土模型（Hardening Soil Model）进行模拟[10-12]。管廊墙体弹性模量E=34.5 MPa，泊松νur=0.2。硬土模型（Hardening Soil Model）能较好地模拟软土和硬土的弹性非线性、硬化/软化特性，并能较好地模拟土体在地震作用下的动力特性，模型参数割线模量、切线压缩模量、以及卸载-再压缩模量可根据经验公式取值；模型应力相关幂指数m取为0.5，卸载-再压缩泊松比νur=0.2[12-13]。

表1 地基土材料特性

数值计算中约束模型底部边界节点的水平和垂直位移，约束模型竖向边界面节点的水平位移。并在模型两个竖向边界设置吸收边界以进一步降低杂波反射。

计算过程中分为两阶段进行：第一阶段在生成地基应力后，开挖管廊内部土体并同时激活BEAM单元模拟管廊施工，计算至数值模型达到力学平衡和变形稳定；第二阶段在模型底部通过对模型施加Kobe地震波相应的加速度模拟地震过程，计算至管廊和地基内力平衡和变形稳定。

3 计算结果分析

3.1 加速度及位移时程分析

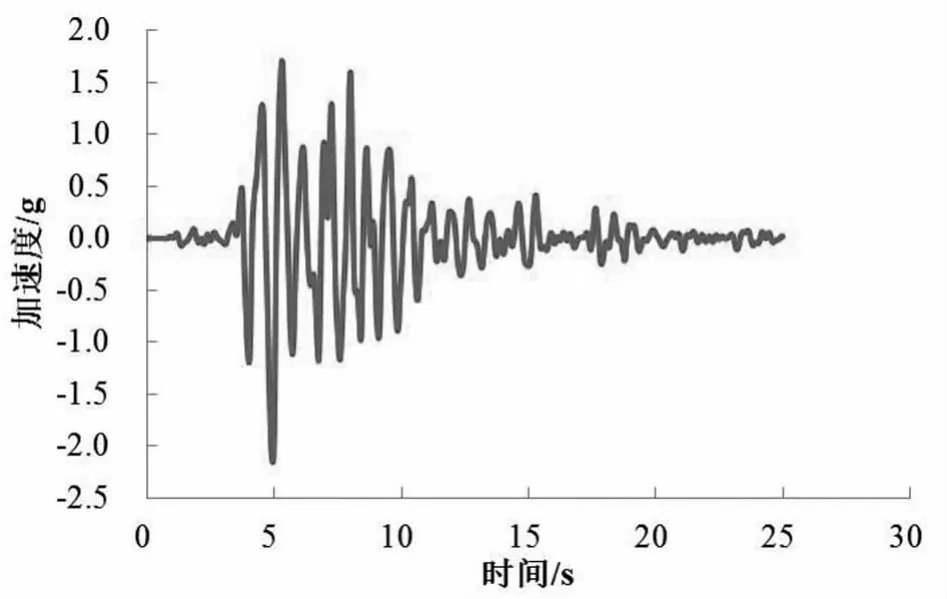
图4 管廊顶板节点加速度时程曲线

图4 为数值计算的管廊加速度时程曲线。由图可见，管廊最大加速度为2.15g，为Kobe地震波最大加速度的2.7倍，即地基对地震加速度有明显的放大作用。管廊最大加速度出现在4.94 s，发生在Kobe地震波最大加速度4.70 s之后，存在一定滞后效应。

图5为管廊位移时程曲线，由图可见，管廊在4.9 s时产生了约6.2 cm的水平位移；地震结束后管廊偏离平衡位置约4.0 cm。

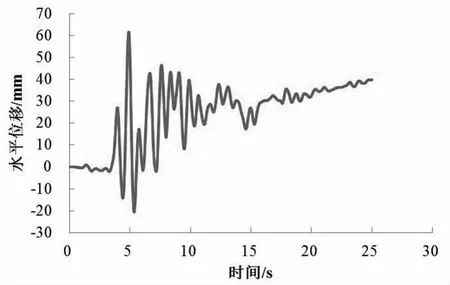
图5 管廊顶板节点位移时程曲线

3.2 墙板弯矩

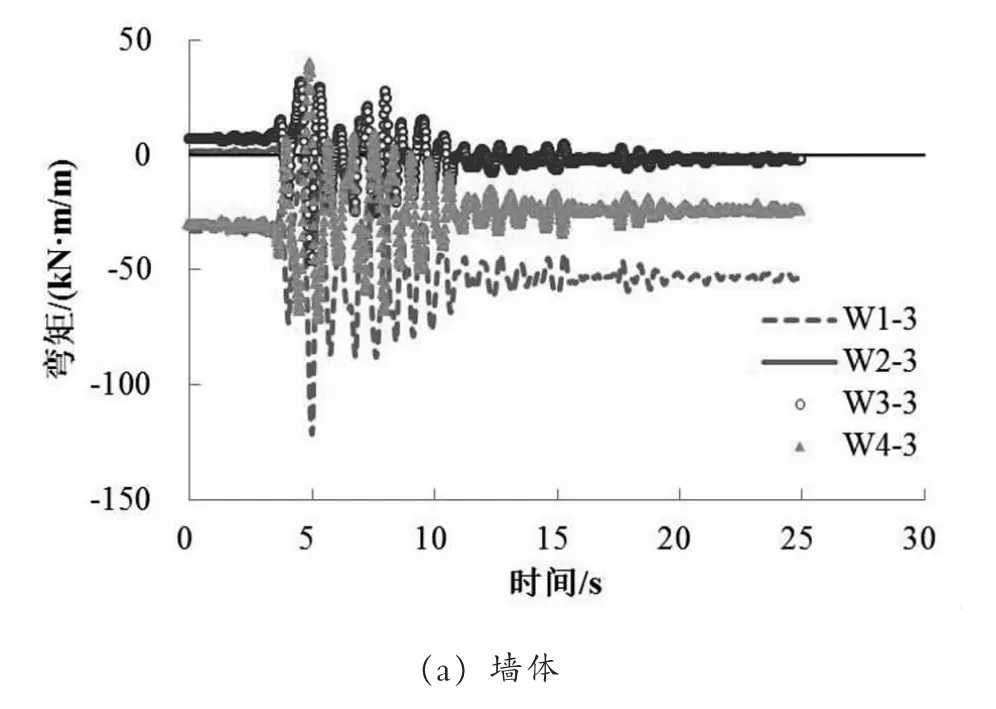
图6给出了地震作用下管廊B1、B2和B3舱墙板特征点的弯矩历时曲线，t=0 s时弯矩初始值为静力状态下地基和管廊自重引起。本文约定，对于管廊外墙、顶板和底板，正弯矩表示结构内侧受拉，负弯矩表示外侧受拉；对于管廊中墙，正弯矩表示结构左侧受拉，负弯矩表示右侧受拉。由图可见，地震作用下管廊外墙弯矩明显大于内墙，B1舱由于结构宽度略大于B3舱，其外墙弯矩也相对较大；B1和B3舱底板弯矩明显大于B2舱，而B1舱底板弯矩也略大于B3舱。偏于安全，下面主要对B1舱管廊结构受力进行分析。

图7给出了在地震作用下B1舱墙板弯矩历时曲线，图中正弯矩表示结构内侧受拉，负弯矩表示外侧受拉，t=0 s时弯矩初始值为静力状态下地基和管廊自重引起。由图可见，静力状态下，B1舱外墙、顶板和底板在跨中为内测受拉，节点处为外侧受拉，最大负弯矩出现在边墙和底板节点处，约为35.2 kN·m/m，最大正弯矩位于边墙跨中，约为38.2 kN·m/m；中墙受力基本对称，故弯矩初始值很小。在地震作用下，管廊墙板弯矩随地震作用变化明显，边墙和底板节点的负弯矩绝对值在4.98 s时达到最大，为139.0 kN·m/m，是静力状态下的3.9倍；边墙跨中正弯矩最大达到57.7 kN·m/m，是静力状态下的1.5倍。

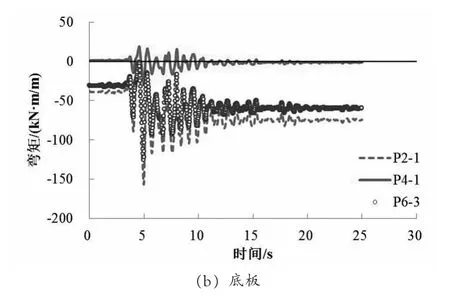
图6 管廊三舱墙板弯矩历时曲线

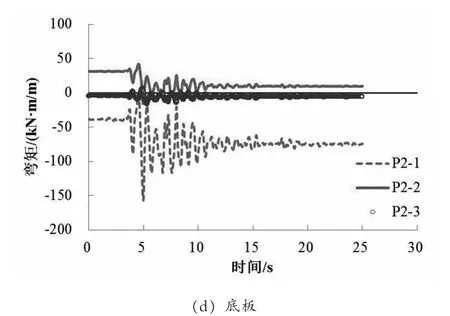
图7 B1舱墙板弯矩历时曲线

3.3 墙板压力

图8 给出了地震作用下B1舱墙板压力历时曲线，负值表示墙板受压。由图可见，静力状态下，边墙压力为179.0 kN/m，中墙压力为326.7 kN/m，显著大于边墙压力，这是由于中墙分担的管廊上覆土体荷载面积大于边墙；底板压力为148.9 kN/m，顶板压力为94.5 kN/m，均小于边墙和中墙压力。在地震作用下，管廊中墙压力随地震作用变化不大，而边墙、顶板和底板的最大压力可分别达到261.5 kN/m、161.1 kN/m和 261.4 kN/m，即分别达到静力状态下的1.5、1.7和1.8倍。

4 结论

本文建立了三舱综合管廊有限元数值模型，分析其在静力和地震作用下的动力响应和受力特性，得出以下主要结论：

（1）地基对地震加速度有明显放大作用，管廊最大加速度为Kobe地震波最大加速度的2.7倍，且存在一定滞后效应；地震过程中管廊最大水平位移为6.2 cm，地震结束后管廊偏离平衡位置约4.0 cm。

（2）静力状态下，管廊墙板节点最大弯矩位于边墙和底板交点，最大跨中弯矩位于边墙；在地震作用下，管廊墙板弯矩随地震作用变化明显，边墙和底板节点弯矩最大值达静力状态下的3.9倍，跨中弯矩最大值为静力状态下的1.5倍。

（3）静力状态下，管廊中墙由于荷载分担面积较大，其竖向压力大于边墙；在地震作用下，管廊中墙压力随地震作用变化不大，而边墙、顶板和底板的最大压力可分别达到静力状态下的1.5、1.7和1.8倍。

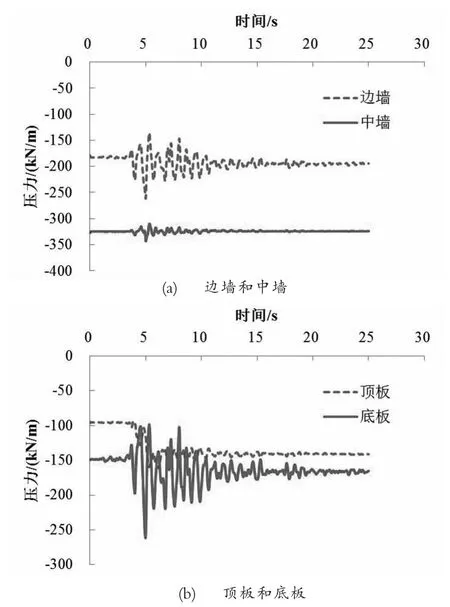
图8 B1舱墙板压力历时曲线

（4）地震作用下综合管廊设计可采用拟静力方法，即将静力状态下计算的管廊墙板弯矩和压力乘以放大系数后进行抗弯和抗压承载力验算。