基于神经网络探究标签依赖关系的多标签分类

宋 攀 景丽萍

(交通数据分析与挖掘北京市重点实验室(北京交通大学) 北京 100044) (16120413@bjtu.edu.cn)

随着计算机技术的发展和广泛应用，文字、图片、视频等多种形式的数据持续产生并呈现爆炸式的增长.近些年，多标签分类受到许多研究人员的关注.传统的分类模型假设实例只属于一个特定的类别，其本质是学习一个从特征空间到标签空间的映射：f(x)→y,即对给定实例x预测其相对应的标签y.这种分类学习也称为单标签分类学习.然而在大多数实际分类任务中，一个实例往往可能同时属于多个类标签.例如，在文本分类中，一篇文本可能同时属于政治、经济、体育等多个主题；在场景分类中，一幅图片可能同时属于室外、城市、日落等多个场景.针对这类数据，分类任务也相应地变为预测一个实例可能具有的多个标签，该分类学习称为多标签分类学习.

尽管在过去的研究中，多标签学习已经得到了广泛关注并取得了一系列的进展，但仍存在若干问题和挑战有待于进一步的深入研究并解决.其中，如何学习和利用多个标签之间的依赖关系是目前被普遍认可和关注的一个关键问题.例如，在场景分类中，沙滩场景往往也是室外场景，一篇娱乐新闻报道则不太可能属于政治新闻.有效地学习和利用这些依赖关系是提高多标签分类模型性能的关键.尽管研究人员已经提出了多种学习和利用标签间依赖关系的方法，但目前关于标签之间的依赖关系并没有明确统一的定义.

在本文中，我们基于神经网络结构提出了一种探究标签之间依赖关系的算法，用以提升多标签分类算法的性能.该神经网络由单隐层构成，并且可以利用深度学习中的先进技术提升网络性能.

本文的主要贡献可归纳为3部分：

1) 在神经网络顶层加入表示语义标签类之间的相似性度量矩阵Ω∈L×L，刻画标签之间的依赖关系.

2) 基于标签之间的依赖关系处理标签缺失问题.

3) 构建3层网络结构,结构简单,能够有效避免复杂网络结构所引发的梯度不稳定性问题.

1 问题描述

1.1 问题定义

最直观的想法是对每个标签类独立地训练一个分类器，但是这样独立的训练策略不能够探索标签之间的依赖关系.为了打破这样的限制，本文提出了基于神经网络探究标签依赖关系的多标签分类算法,该算法在输出层增强了不同语义标签之间的知识共享.

1.2 相关工作

在多标签学习问题中，每个实例同时与多个标签相关联.已有的算法大体可以分为2类：基于问题转化的方法和算法适应性方法.

二元关联(binary relevance, BR)、分类器链(classifier chains, CC)是典型的基于问题转化的方法.由Boutell等人[1]提出的BR算法将多标签学习问题转换为多个独立二分类任务，每个二分类器对测试样本预测出一个可能的标签，根据得分函数给出标签得分,并将其排列，用最大后验概率(MAP)原理来选择一个或多个类来作为测试样本的标签.BR算法的典型缺点是它假设标签之间是相互独立的，忽视了标签之间的潜在联系，从而导致算法性能不佳.考虑到标签之间潜在的相关性,Read等人[2]提出CC算法，该方法同样将多标签学习问题转换为二分类问题，同时认为当前预测的标签存在与否对下一个标签的预测存在一定的影响.该算法为每个类别训练一个分类器，根据标签的顺序构成一个分类器链，从第2个分类器开始,后一个分类器都是基于前一个分类器的预测结果构建的.也就是说，在样本通过第2个分类器时，必须将样本特征与第1个分类器预测出来的标签合起来作为样本新特征通过第2个分类器，以后的分类器按照此方法通过，最终得到样本的所有标签.但CC方法存在一个问题，当对之前的标签预测错误时，该错误会沿着分类器链传导到链末端，导致分类性能下降.为了降低标签顺序对分类效果的影响，Read等人[2]在此基础上进行一定的改进，加入集成的思想，提出集成分类器链(ECC)算法，构建多条分类器链，根据多条分类器链的结果采用多数投票法最终得到样本的所有标签.除了典型的BR和CC算法，Brinker[3]提出的标准标签排序(calibrated label ranking, CLR)算法将多标签学习任务转化为标签排序任务.Tsoumakas和Vlahavas[4]提出的Randomk-labelsets算法则直接将多标签学习任务转化为多类别学习任务.

算法适应性方法采用学习技术来处理多标签问题，是最主要的解决多标签问题的途径.Zhang和Zhou[5]提出的ML-kNN算法采用懒惰学习技术，Clare和King[6]提出的ML-DT算法采用决策树技术，Elisseeff和Weston[7]提出的Rank-SVM算法采用核技术，Ghamrawi和Mccallum[8]提出的CML算法则采用信息论技术.为了应对超高维多标签学习问题,基于嵌入技术的算法[9-10]和基于树技术的算法[11-13]大量涌现.然而，大多数的多标签学习算法[14-21]都集中在探索标签相关性或依赖信息，以提升分类预测的性能.Jing和Yang等人[14]提出基于半监督映射学习的SLRM算法来探究标签相关性，对映射矩阵U进行SVD分解，U的左奇异矩阵表示标签之间的相关性；Li和Zhao等人[15]提出条件受限波尔兹曼机来探究标签依赖关系，它在标签输出层和隐层之间构建受限波尔兹曼机，位于特征输入层之上，利用波尔兹曼机的固有性质学习标签依赖关系，将一个无向图模型转换为条件概率模型求解.Zhang和Yeung[16]提出刻画多任务关系的凸优化形式MTRL算法，同时学习映射函数和任务之间的依赖关系矩阵Ω.Ciliberto和Mroueh等人[17]提出基于多任务结构的凸优化学习算法，用以刻画任务之间的依赖关系，该算法将标签关系矩阵作为惩罚函数的参数.

标准的多标签分类算法都假设训练数据是标签完备的.这种假设在许多现实应用中不成立，由于标签的收集非常困难，因此标签不完备的数据普遍存在.为了处理标签缺失问题涌现出了大量的算法[14,22-26].Lin和Singh等人[22]提出基于后验概率正则化的PRLR算法，分别从构造映射矩阵Q和计算后验概率P来预测标签，同时使KL散度尽可能的小.Jing和Yang等人[14]提出的基于半监督映射学习的SLRM算法能够基于数据获得固有的数据结构，从而可以解决标签缺失问题.Yu和Jain等人[26]提出一个通用的经验风险最小化框架来处理大规模多标签分类任务，但是仅在标签完备的数据上训练模型来应对标签缺失问题，没有充分考虑标签缺失数据在训练模型中的重要性.

为了进一步提升多标签分类预测模型的性能，本文提出基于神经网络探究标签依赖关系的多标签分类算法，通过在神经网络的顶层加入一个标签依赖关系矩阵来刻画标签之间的相关性，同时根据标签依赖关系还可以解决带有标签缺失数据的多标签分类问题.

2 基于神经网络的多标签分类算法

在本节中,主要介绍基于神经网络探究标签依赖关系的多标签分类算法的细节.

2.1 基本模型

基于神经网络探究标签依赖关系算法模型如下：

(1)

其中，JCE是交叉熵损失函数，用来评估给定训练样本的真实标签和预测结果之间的误差;Φ(f)是正则项，用来控制f的复杂性，防止过拟合;λ是正则化参数，用来平衡目标函数中2项在相同的数量级.

2.2 交叉熵损失函数

本文中，使用交叉熵作为损失函数，它被广泛用于神经网络分类训练任务.其表达式为

(2)

其中，on l和yn l分别表示对标签l的预测结果和真实标签.

2.3 神经网络结构

受生物系统的启发，神经网络由大量的神经元相互连接而成，用以模仿神经系统中的信息处理过程.通过多层神经元级联，神经网络具备强大的非线性抽象能力，并且当给定足够多的数据时，它能够学到从输入空间到输出空间的任意映射.

本文构建的神经网络结构包含3层，分别是输入层、单隐层和输出层.神经网络结构如图1所示.单隐层有F个神经元，输入单元通过权重W(1)∈F×D和偏置项b(1)∈F×1与隐层单元h∈F×1 连接.隐层单元h∈F×1 通过权重W(2)∈L×F和偏置项b(2)∈L×1 与输出单元o∈L×1 连接.因此该网络能够被写成矩阵形式.本文构建一个前馈网络fθ:x→o，作为范围在[0,1]之间非线性函数的混合：

fθ(x)=fo(W(2)fh(W(1)x+b(1))+b(2)),

(3)

其中θ={W(1),b(1),W(2),b(2)}，fo和fh分别是输出层和隐层的激活函数，因此函数fθ被重写如下：

z(1)=W(1)x+b(1),h=fh(z(1)),

(4)

z(2)=W(2)h+b(2),o=fo(z(2)),

(5)

其中，z(1)和z(2)分别表示输入层激活和隐层激活的权重之和.

Fig. 1 Neural network with a single hidden layer of two units图1 含有2个隐单元的单隐层神经网络模型

本文的目标是寻找使得损失函数J(θ;x,y)最小化的参数θ.这个损失函数评价网络预测的标签和真实标签之间的差值.

2.4 标签依赖关系学习

正如1.2节所讨论的，探索标签之间的依赖关系非常重要，能够提高模型预测性能.因此，本文提出基于神经网络探究标签依赖关系的多标签分类算法.为了加强标签之间的知识共享，本文拓展之前的目标函数为

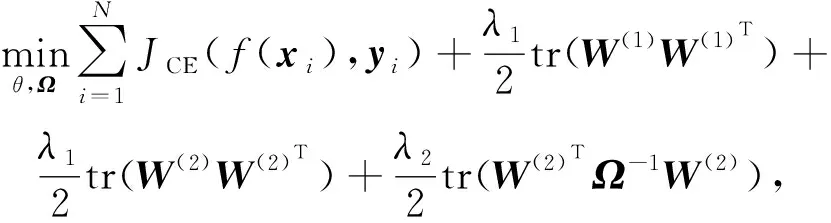
(6)

s.t.ATΩA≥0，tr(Ω)=1，

其中A为任意非零向量.

本文期望在学习预测模型的同时学习标签之间的相关性，尤其是，该目标函数是凸函数，加入一个迹形式的正则项，其中输出层的权重W(2)与标签依赖关系矩阵Ω∈L×L的乘积作为迹范数的参数.约束ATΩA≥0 表明标签之间的依赖关系是半正定的，因为它可以被理解为语义标签类之间的相似性度量.系数λ1和λ2是正则化参数，用来平衡不同正则项的贡献度.

随着深度学习快速发展，出现大量的技术能够有效地克服训练神经网络的困难，其中，Dropout技术可以避免由大量参数空间导致的过拟合现象，因此得到最终的目标函数为

(7)

其中，A为任意非零向量，λ1是正则化参数，约束tr(Ω)=1 用来防止复杂度过高.

3 优化方法

3.1 优化过程

对于式(7)提出的目标函数，采用最小批梯度下降方法(mini-batch gradient descent, Mini-batch-GD)求解该优化问题，寻找使得损失函数最小化的参数W(1),b(1),W(2),b(2),Ω.

首先考虑当Ω固定时,原优化问题变成下列无约束的优化问题：

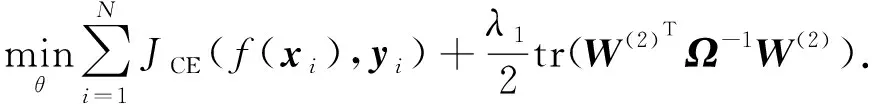
(8)

接下来介绍当其他参数固定时，对标签依赖关系矩阵Ω的更新.公式可以被重写为

(9)

其中，A为任意非零向量.

根据Cauchy-Schwarz不等式，式(9)的闭式解:

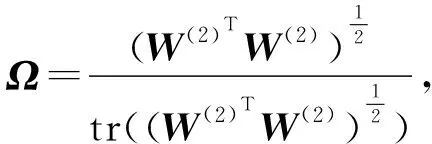
(10)

首先初始化Ω=(1m)Im，表示假设起初所有的标签之间是相互独立的.

3.2 AdaGrad的自适应学习率

最小批梯度下降方法(Mini-batch-GD)是简单但有效的求解目标函数最小化的技术.当采用Mini-batch-GD为优化方法时，一个重要的问题是学习率的选择.

引，η0表示初始学习率.

在多标签学习中，常见的情况是很少一部分标签经常出现，而大部分标签只是偶尔出现，因此对所有的变量进行梯度更新时采用固定相同的学习率是不合适的.如果使用AdaGrad自适应学习率，对于频繁出现的标签更新时学习率会很小，而对罕有出现的标签更新时学习率会较大，从而可以精确收敛.

4 实验与结果

4.1 评价标准

为判断学习算法的性能优劣，首先需要确定评价标准.根据多标签数据的分类结果可以分为2种类型：1)基于标签排序，按样本属于各标签的可能性对所有标签进行排序，并形成一个排序结果；2)基于结果标签集合，其中每个元素都是分类器对其预测的标签.

基于标签排序的评价标准：1)单一错误(One-error).统计预测的标签序列中排在最前面的标签不是真实标签样本的比例,值越小表明分类器的性能越好.2)覆盖值(Coverage).统计在预测的标签序列中，从序列的第1个元素出发，为了找出样本所有的相关标签需要走的平均步数，值越小表明样本的真实相关标签在预测标签序列中的位置越靠前，分类器的性能越好.3)序偶损失(Rankloss).统计在预测标签序列中两两标签之间，当前测试样本的不相关标签排在相关标签之前的次数，值越小表明分类器的性能越好.4)平均精确率(average precision).针对样本的每个相关标签，平均精确率统计了在样本的预测标签序列中排在它前面的相关标签的个数，然后在所有样本的所有标签上求均值，值越大表明分类器的性能越好.

基于结果标签集合的评价标准：1)召回率(Recall).统计样本真实标签集中的被预测到的标签的比例，值越大表明分类器的性能越好.2)精确率(Precision).统计预测标签集中为当前样本真实标签的标签比例，值越大表明分类器的性能越好.3)F1测量(F1 measure).平衡了精确率和召回率，值越大分类器的性能越好.4)准确率(Accuracy).统计每个真实标签集和预测标签集的交集大小与真实标签集和预测标签集的并集大小的比值，并在样本上求均值，值越大分类器正确分类的程度越大.5)AUC.表示相关标签排在不相关标签前面的概率,值越大表明分类器的性能越好.

4.2 数据集

为充分比较和验证所提出算法NN_AD_Omega的有效性，本文共挑选了4个已经被广泛采用的多标签数据集开展实验.这4个数据集分别为MSRC①,SUN②,Delicious③和CAL500③.MSRC是典型的基于词包采样的图像数据集，而SUN是典型的基于图像低层特征采样的数据集.Delicious和CAL500数据集能够直接从Mulan网站中被下载.

表1给出了这4个数据集的具体描述，其中N表示数据集样本数量，D表示特征维数，L表示标签数量，Cardinality定义每个样本平均标签个数.在这4个数据集中，标签数量的范围是23～983，每个样本平均标签个数的范围是2.508～26.044，因此对这些数据集进行标签预测是具有挑战性的任务.

Table 1 Multi-Label Dataset Summary表1 多标签数据集描述

4.3 对比算法和参数设置

为了充分验证NN_AD_Omega算法的性能,本文选择NN_AD[27],CRBM[15],C2AE[21]这3种典型算法作为比较对象.这3种算法代码均在Matlab中被实现,运行在4 GB内存搭配2 GHz CPU的Windows系统中.

NN_AD算法基于神经网络结构解决多标签分类问题,采用AdaGrad技术和Dropout 技术保证快速收敛.CRBM算法基于条件玻尔兹曼机模型探究高阶标签之间依赖关系解决多标签分类问题，同时解决标签缺失问题.C2AE算法基于自编码器模型探究标签依赖关系解决多标签分类问题.相关参数的具体设置取自原论文[27].

NN_AD_Omega算法基于单隐层神经网络，隐层的神经元个数为1 000，隐层的激活函数为Relus，输出层的激活函数为Sigmoid，学习率η0初始范围为{0.001,0.01,0.1}.为了模拟标签缺失情况,针对每个数据集随机选择一个训练集的标签缺失率σ,σ∈{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9}.

4.4 算法收敛性

为了研究算法的收敛性,在2个数据集上得到目标函数的值,如图2所示.随着迭代次数的增加,目标函数的值会不断地减小,并且在迭代一定次数之后目标函数的值会趋于稳定.

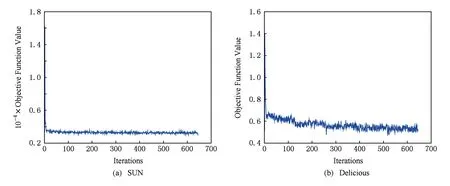
Fig. 2 Convergence of NN_AD_Omega on SUN and Delicious图2 NN_AD_Omega算法在SUN和Delicious数据集上的收敛性

4.5 对比算法的性能表现

为了充分验证NN_AD_Omega算法与对比算法的性能，本文在选定的4个数据集上进行大量的实验，表2给出结果的平均值，每个评价指标的最优值用粗体标明.

根据表2中的结果,我们可以得出4个结论：

Table 2 Comparison of Multi-Label Learning Performance Output by Four Algorithms on Four Datasets表2 4种算法在4个数据集上的性能表现

Continued (Table 2)

Notes:“↑” means the larger the value, the better the performance; “↓” means the smaller the value, the better the performance.

1) NN_AD_Omega算法优于仅仅基于神经网络结构的NN_AD算法,表明探究标签之间的依赖关系对于多标签学习任务是至关重要的.

2) NN_AD_Omega算法优于基于条件玻尔兹曼机的CRBM算法,表明在神经网络顶层加入Ω矩阵来刻画标签之间的依赖关系比基于玻尔兹曼机自身属性来构建标签之间依赖关系更为有效.

3) NN_AD_Omega算法优于基于自编码器的C2AE算法,表明构建矩阵Ω∈L×L具有丰富的标签依赖信息,基于自编码器构建标签依赖关系会丢失部分的标签依赖信息.

4) 为了验证NN_AD_Omega算法学到的标签之间的依赖关系矩阵Ω,表3给出了MSRC数据集与每个标签最相近的2个标签.正如所期望的,算法预测的标签确实与给定的标签语义相关.

Table 3 Label Correlation Identified by NN_AD_Omega on MRSC Data表3 NN_AD_Omega算法从MRSC数据集得到的标签依赖关系

4.6 标签缺失的性能表现

为了进一步研究NN_AD_Omega算法在标签缺失情形下的性能表现，本文在CAL500数据集上进行实验.对于数据集中的每个实例,通过变化缺失标签的比例来模拟标签缺失情形,缺失的标签包括正标签和负标签.为了避免出现空标签类和一个实例仅含有负标签的情况,处理数据时必须保证每个标签类至少有一个实例,每个实例至少有一个正标签.因此,yi j=0表示第i个实例的第j个标签缺失,yi j=1表示第i个实例包含第j个标签,而yi j=-1表示第i个实例不包含第j个标签.实验中,选取不同的σ值进行缺失模拟，所有的性能指标是多次实验的平均值，前3种算法的性能对比，如图3所示:

Fig. 3 Comparison results of three algorithms under varying the ratio of missing entries on CAL500图3 3种算法在CAL500数据集上标签缺失情形下的性能表现

通过图3可以看出，随着标签缺失率的增大，这3种算法的性能会逐渐降低，表明标签信息的缺失会降低多标签分类的性能.从总体上来看，NN_AD_Omega算法要优于NN_AD和CRBM，表明NN_AD_Omega算法相较于NN_AD和CRBM学到了更有效的标签依赖关系.因此，NN_AD_Omega 算法能够有效地处理标签缺失问题.

5 结论与展望

为了解决多标签分类任务,本文提出了一种新模型NN_AD_Omega,该模型能够有效学习从特征空间到标签空间的映射.通过在神经网络顶层加入Ω矩阵,NN_AD_Omega模型能够有效地探究标签之间的依赖关系.同时,NN_AD_Omega模型也能够充分地利用标签之间的依赖关系处理标签缺失问题.为了快速高效地优化该模型,本文采用最小批梯度下降方法(Mini-batch-GD)求解.大量的实验表明,NN_AD_Omega算法性能优于当前已有的先进算法,并且表明NN_AD_Omega算法能够有效地处理多标签分类问题.

在进一步的研究工作中,我们将致力于研究刻画标签之间依赖关系的形式,进一步提升算法性能,以期通过不同的标签依赖关系形式高效、准确地预测标签信息.

SongPan, born in 1994. Master candidate. Her main research interests include machine learning, multi-label learning.

JingLiping, born in 1978. PhD, professor. Member of CCF. Her main research interests include machine learning and high-dimensional data mining.