减隔震小箱梁桥地震响应桩土效应影响的模拟
陈彦坤,袁学伦
(中交第四公路工程局有限公司西安工程设计分公司,陕西 西安 710065)
0 引 言
目前,桥梁减隔震动力分析以非线性时程分析为主,在非线性时程分析中,桥梁下部结构边界条件的选取对于分析结果具有较大影响。常用于模拟下部结构边界条件的方法包括墩底直接嵌固法、nD嵌固法和m法[5]。
本文以采用减隔震技术的某桥梁为背景,分别对比不同地基系数下采用3种边界条件模拟方法时的时程分析结果[6]。
1 理论依据


式中:[M]为整体质量矩阵[7];[C]为阻尼矩阵;[K]为结构总刚度矩阵。
直接嵌固法在计算桥梁结构的地震影响时,不考虑桩基础的影响,直接在墩底固结。
nD嵌固法考虑部分桩基础对桥梁结构力学响应的影响,在地表或一般冲刷线下某一深度将桩基础固结[8]。
嵌固深度
据此,法院依据《劳动合同法》第87条、《最高人民法院关于民事诉讼证据的若干规定》第2条、《最高人民法院关于审理劳动争议案件适用法律若干问题的解释》第13条之规定,判决公司于判决生效之日起10日内支付成锐违法解除劳动合同赔偿金48802元、延时加班费1406元。驳回成锐的其他诉讼请求。
式中:m为地基系数;b0为桩基础的计算宽度;EI为桩基础的计算刚度,η2取值为2.5[9]。
m法将桥梁结构与桩基础共同考虑,将桩周土体对基桩的作用模拟为沿深度变化的一系列弹簧[10]。
2 项目背景
某桥位于青海省南部,跨径组合为(4×20+5×20+5×20+5×20+5×20+5×20+5×20+3×20)m。桥梁起点桩号为K174+393.78,终点桩号为K175+140.22,全长746.4 m,宽12 m。桥梁上部结构采用预应力混凝土预制箱梁,梁高1.2 m,桥梁下部结构采用双柱式桥墩,柱径为1.3 m,柱接桩,桩径为1.5 m。
3 基本模型
本文采用有限元分析软件Midas Civil 2012建立该桥第2联5×20 m预应力混凝土预制箱梁的全桥空间有限元模型,主梁和桥墩均采用三维梁单元,横隔板荷载和二期恒载作为梁单元附加质量。建立的桥梁地震动力分析有限元模型如图1所示。

图1 结构分析有限元模型
桥梁下部结构的约束条件分别采用m法、nD嵌固法和墩底固结法进行对比分析,m值分别采用规范所规定的不同类型土的临界值[11]。具体数值及相应nD嵌固法的嵌固深入如表1所示。

表1 地基系数m及相应嵌固深度
主梁与桥墩根据实际支座类型建立非线性连接。坐标系取顺桥向为X轴,横桥向为Y轴,竖向为Z轴。地震时程分析时,按照瑞利阻尼模型选取结构阻尼,其中计算瑞利阻尼的第一阶振型为结构的基本振型,第二阶振型取有效质量率最大的振型[12]。
4号、9号过渡墩采用HDR-D250-H/8支座,5~8号墩采用HDR(Ⅱ)-D350-G10/8支座。
HDR高阻尼隔震橡胶支座可简化为双线性恢复力力学模型,如图2、3所示。
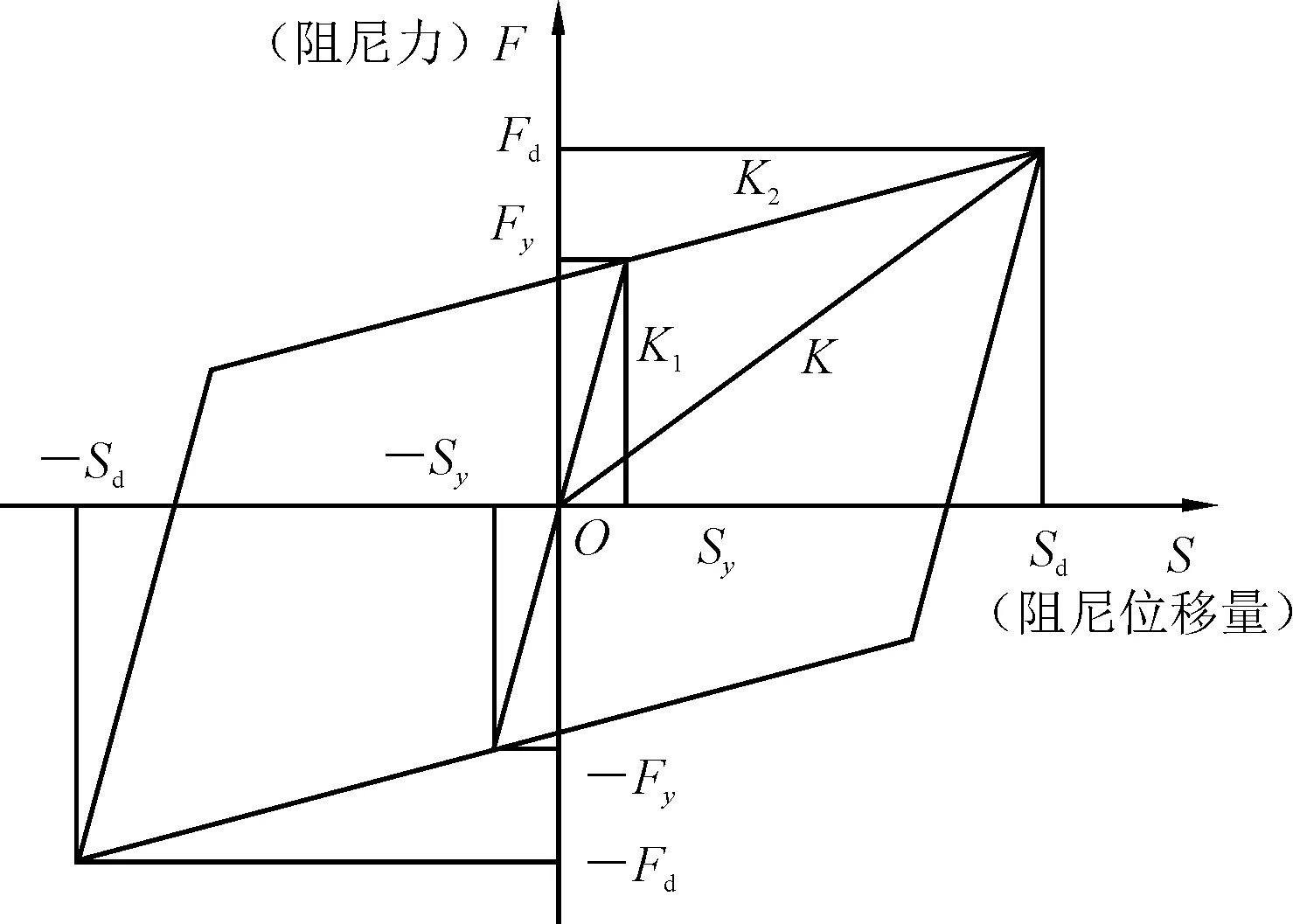
图2 HDR固定型支座双线性恢复力力学模型

图3 HDR滑板型支座双线性恢复力力学模型
图2、3中:K1为屈服前刚度;K2为屈服后刚度;Sy为屈服位移量[13];Sd为设计阻尼位移;Fy为屈服力;Fd为设计阻尼力;K0为屈服前刚度;X0y为屈服位移;F0y为滑动摩擦力。
依据《公路桥梁抗震设计细则》(JTG/T B02-01—2008),该项目桥梁属于B类桥梁,项目地震波峰值加速度为0.15g。本文所采用地震波时程曲线如图4所示。

图4 地震波时程曲线
4 非线性时程分析
4.1 纤维截面划分
由于该桥所处地区地震烈度较大,在E2地震作用下,结构已进入塑性状态[14],采用传统弹性方法进行结构分析已无法反映结构在地震作用下的实际受力状态,故本文在结构墩底塑性铰区采用纤维截面模拟结构实际受力状态。纤维截面划分如图5所示。

图5 桥墩塑性铰区纤维截面分割
4.2 结构自振周期分析
本文分别采用m法、nD嵌固法及墩底固结法进行工程实例桥自振周期的计算,结果如表2~5所示。
采用不同方法模拟桩土效应时,结构自振周期计算差异(以m法为基本值,表示nD嵌固法与墩底固结法与其差异系数)如图6所示。

表2 m为5 000 kN·m-4时结构前5阶周期 s
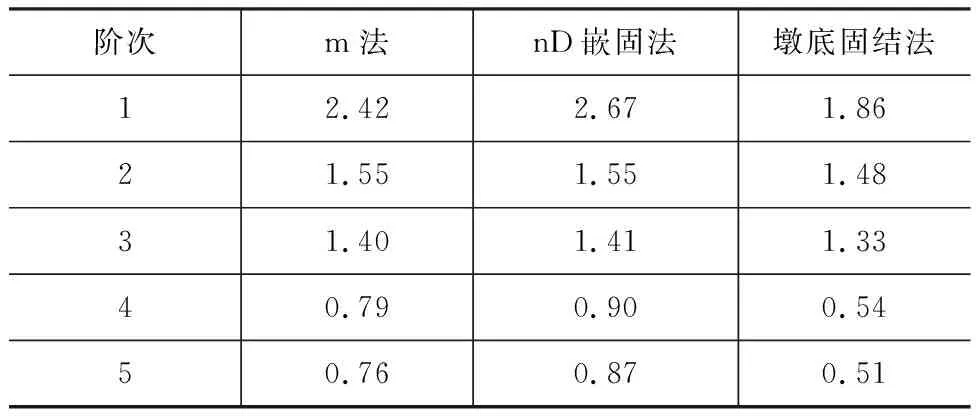
表3 m为10 000 kN·m-4时结构前5阶周期 s
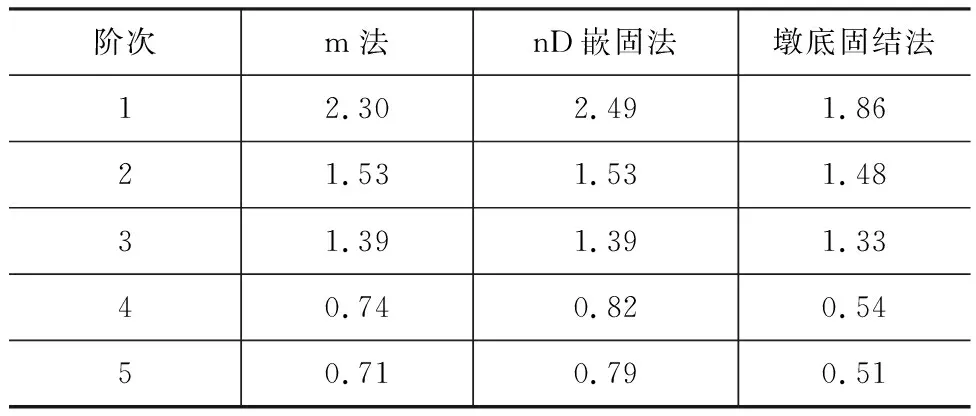
表4 m为30 000 kN·m-4时结构前5阶周期 s

表5 m为80 000 kN·m-4时结构前5阶周期 s
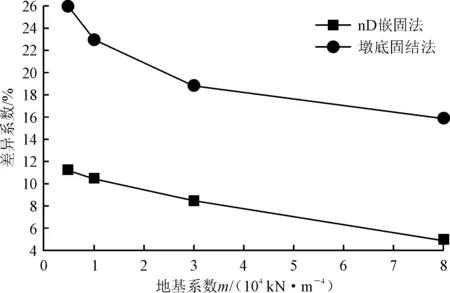
图6 结构自振周期差异系数
由表2~5、图6可知,墩底固结法计算结构自振周期结果与m法计算结构自振周期结果的差异显著大于其与nD嵌固法所计算的结果差异,且采用2种方法计算的周期与m法计算周期都随着地基系数m的增大而减小,在m>80 000 kN·m-4时,nD嵌固法计算结构自振周期与m法的计算结果基本一致。
4.3 塑性铰区弯矩分析
由于篇幅原因,以下仅给出该桥在地震作用下的墩底塑性铰区顺桥向弯矩[15],如表6~9所示。
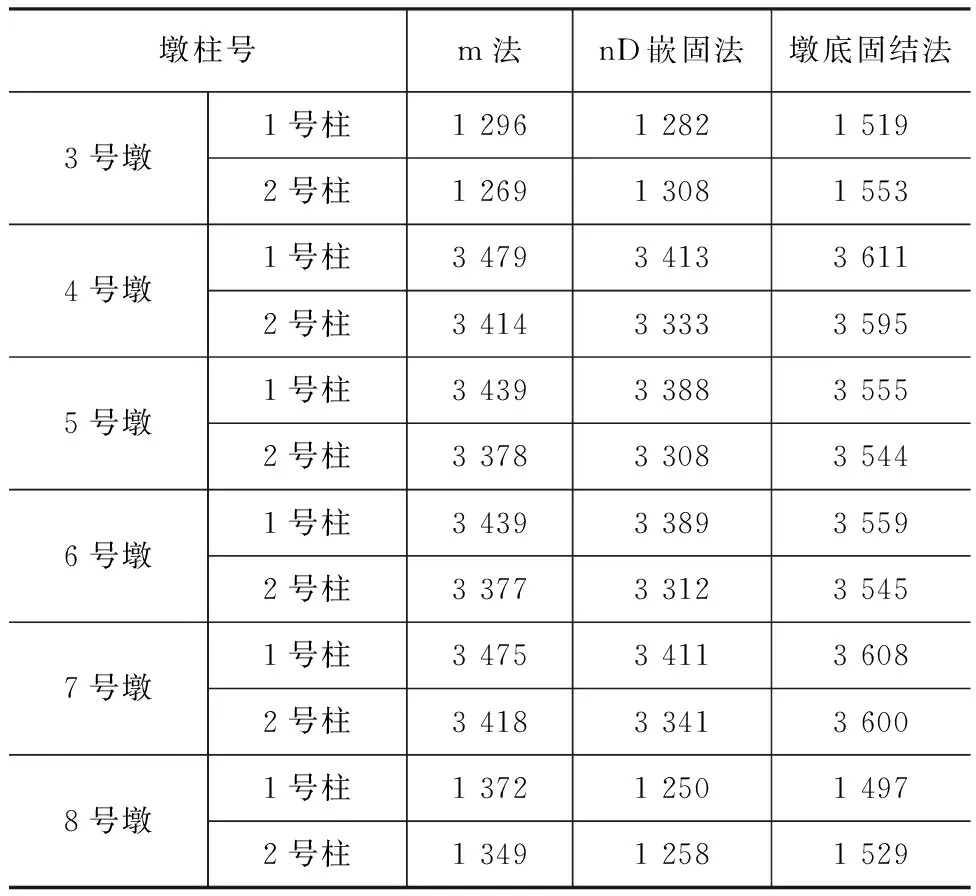
表6 m为5 000 kN·m-4时塑性铰区顺桥向弯矩kN·m
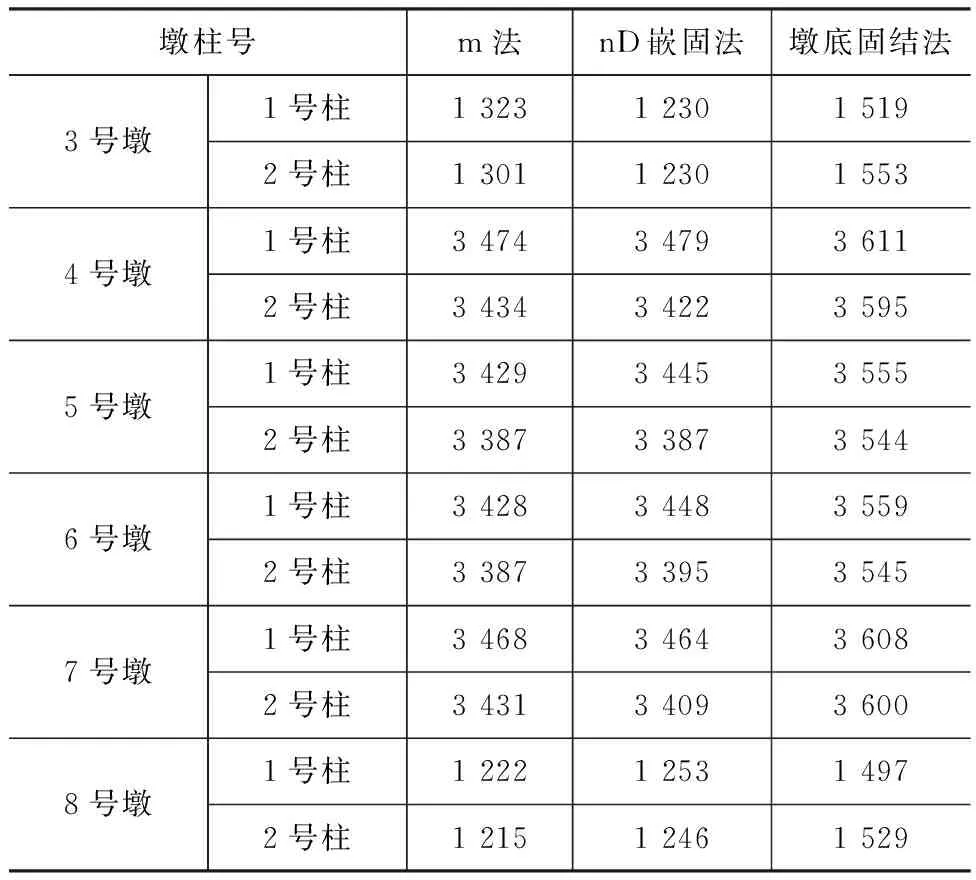
表7 m为10 000 kN·m-4时塑性铰区顺桥向弯矩kN·m
采用不同方法模拟桩土效应时,墩底塑性铰区顺桥向弯矩最大差异[16](以m法为基本值,nD嵌固法与墩底固结法与基本值的差异系数)如图7所示。
由图7及表6~9可知,采用墩底固结法计算结构墩底塑性铰区的顺桥向弯矩与m法计算结果的差异显著大于其与nD嵌固法计算结果的差异,墩底固结法与m法的计算结果最大差异大于20%,nD嵌固法与m法的计算结果最大差异小于10%。m>80 000 kN·m-4时,nD嵌固法的计算结果与m法的计算结果基本一致。
4.4 结构地震响应位移分析
由于篇幅原因,以下仅给出该桥在地震作用下杜卫华

表8 m为30 000 kN·m-4时塑性铰区顺桥向弯矩kN·m

表9 m为80 000 kN·m-4时塑性铰区顺桥向弯矩kN·m
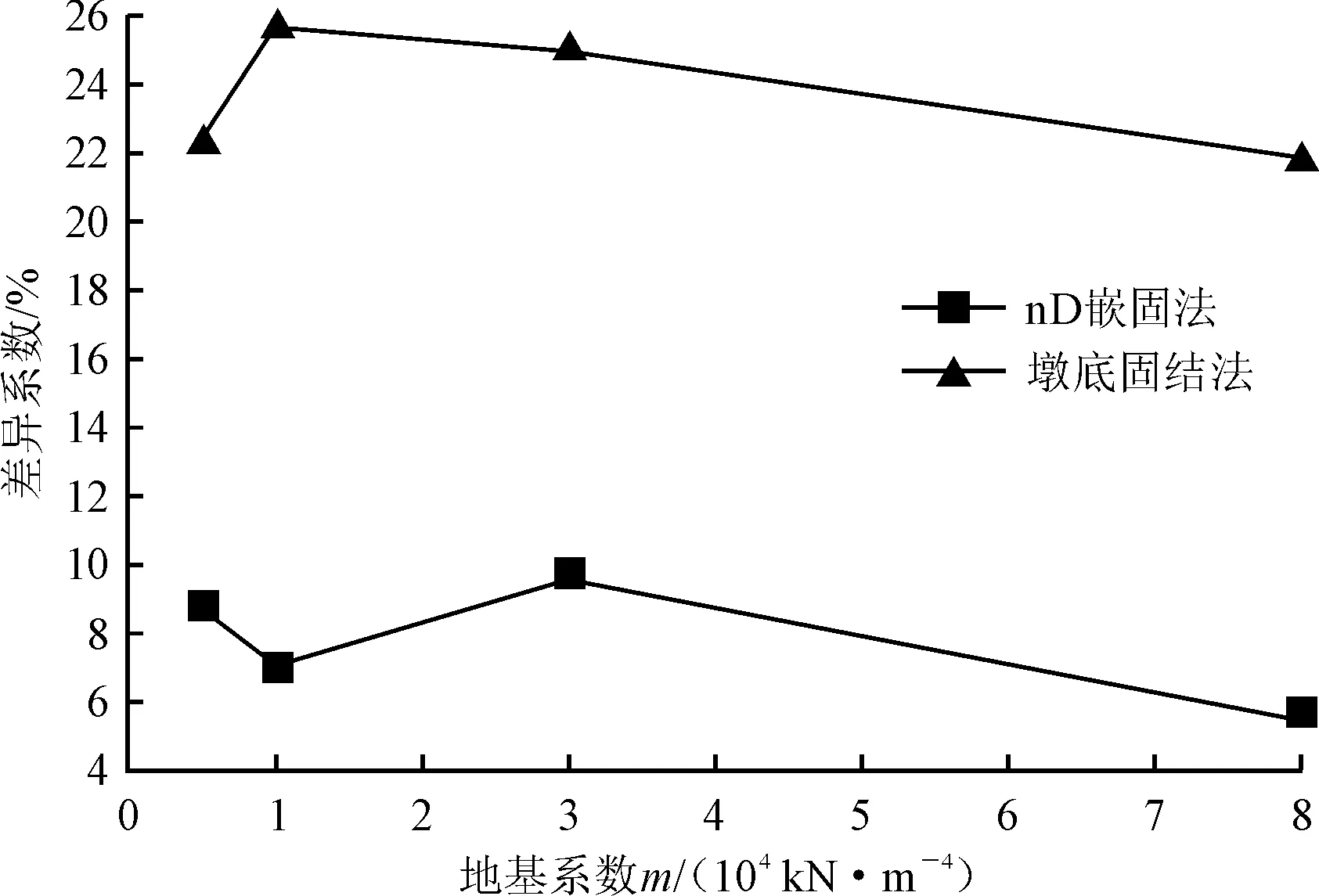
图7 墩底塑性铰区顺桥向弯矩差异系数

图8 主梁顺桥向位移最大差异
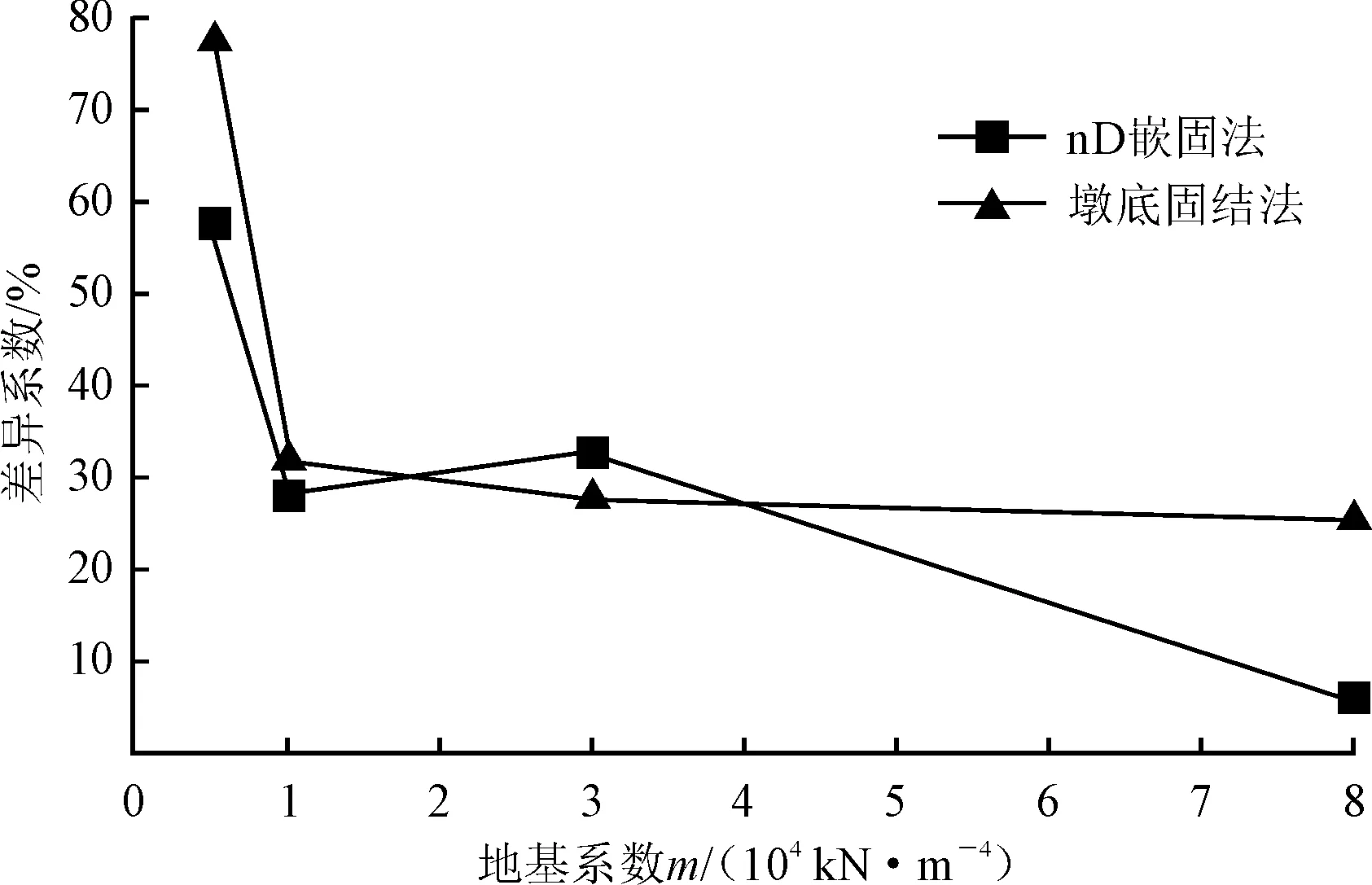
图9 墩顶顺桥向位移最大差异
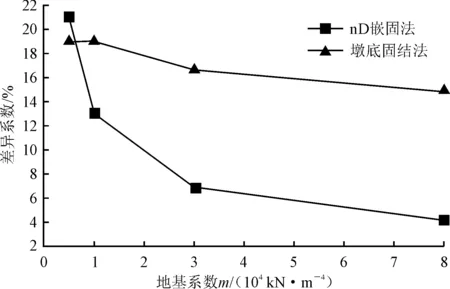
图10 支座顺桥向位移最大差异
由图8~10可知,墩底固结法计算结构在地震作用下的位移情况与m法计算结果的差异显著大于其与nD嵌固法计算结果的差异,墩底固结法与m法计算结果的最大差异大于15%。在m<80 000 kN·m-4时,nD嵌固法与m法所计算的墩顶纵向位移结果差异较大。采用nD嵌固法与m法所计算的主梁纵向位移与支座纵向位移均较小,且在m>80 000 kN·m-4时,采用nD嵌固法的计算结果与m法的计算结果基本一致。
5 结 语
(1)采用墩底固结法与m法进行非线性时程分析时,结构的自振周期、顺桥向弯矩以及结构位移的计算结果差异均大于15%。
(2)nD嵌固法、墩底固结法、m法的计算结果差异随着m值的增大而减小。
(3)在m>80 000 kN·m-4的情况下,采用nD嵌固法与m法进行非线性时程分析的各项计算结果差异均小于5%。
(4)在m>30 000 kN·m-4的情况下,除桥墩纵向位移外,采用nD嵌固法与m法进行非线性时程分析的各项计算结果差异均小于10%。

