基于MMC的直流电网架空线路故障暂态特性分析及快速保护*

谢秋霞

（华南理工大学，广东广州 510641）

0 引言

模块化多电平换流器（Modular Multilevel Converter，MMC）作为一种易拓展、设计灵活、工程实现方便的新型VSC拓扑，尤其适用于高压大功率输电方面[1-2]。由于系统拓扑结构的原因，MMC-HVDC系统对直流线路保护的要求很高[3-4]，因此当前工程中，为了减少线路故障率，一般使用直流电缆作为传输线。然而在大容量远距离直流输电中，采用架空线输电是更为经济合适的选择。因此，分析直流侧架空线路的故障特征，提出更快速可靠的保护方案显得非常必要。

针对MMC型直流系统，目前已有许多关于其直流侧短路特性的研究，例如直流侧双极短路和单极接地故障后的故障电流计算[5-6]、不同换流变压器接线下的不同类型故障的仿真分析[7]等。此类分析对直流线路保护策略的选取具有一定的参考意义，然而其重点均放在换流器的响应部分，着重分析短路电流的大小。而对于架空线路故障而言，由故障行波过程带来的暂态特性是直流线路快速保护原理的基础，因此需要对其进行更深入的分析。

随着混合断路器技术的进步和对直流系统可靠性要求的提高，在线路两侧配置直流断路器的直流电网方案成为了研究热点之一[8-9]。在此类直流网络中，网络单点故障时不再需要停运整个直流系统，而是由直流断路器隔离故障区域，保全健全部分[10]。大容量直流断路器需要限流电抗器配合运行[11]，而限流电抗器作为线路边界的一部分，能为线路快速保护提供思路。结合换流器与线路边界特征，文献[12]提出利用限流电抗器线路侧电压变化率的差异判别区内外故障；文献[13]和[14]基于各电气量的频率特征，分别利用限流电抗器两侧电压的高频量比值和线路电流的高频量大小判别故障，后者还加入了电压变化率作为方向判据。然而，以上保护原理均是在传统VSC型系统的基础上提出，其换流器特性及线路边界特征与MMC型系统均有所不同。文献[15]结合MMC简化模型对电缆线路的故障初始行波波头时域特征进行了分析，进而构成保护判据；而文献[16]则同样利用行波波头时域特征提出了MMC型直流网络架空线路快速保护方案。上述研究着眼于直流线路故障初始行波的波头时域特征，而本文则侧重于直流线路故障暂态过程的频率特征分析，并据此构成相应的快速保护原理。

为此，本文首先介绍了配置直流断路器的MMC-HVDC网络拓扑结构，然后对直流侧架空线路短路故障进行了故障暂态特性分析。在此基础上，利用故障线模电压的高、低频小波能量比值构造区内外故障识别判据，并利用电压地模量识别故障极。最后，在PSCAD/EM⁃TDC中搭建了直流电网仿真模型，验证了所提保护的正确性和有效性。

1 MMC-HVDC网络拓扑

图1为一个四端MMC-HVDC网络示意图，每条线路两端均装设了直流断路器及限流电抗器。任何直流断路器都有一个最大开断电流（Imax），在线路故障电流超过Imax之前，不仅保护系统需要完成故障检测和定位等工作，而且断路器也需要完全开断[3]。由于直流电网阻尼较小，在线路故障尤其是换流器近端故障时，线路电流上升快且峰值大，很容易超过断路器的Imax。因此，为匹配电网容量与断路器的开断能力，需要加入限流电抗器。限流电抗器可以限制故障电流上升率，为断路器争取充足的动作时间[12]。

图1 四端MMC-HVDC直流网络示意图

2 直流线路故障特征分析

2.1 MMC换流器等值模型

当MMC-HVDC系统发生直流线路极间故障时，处于投入状态的子模块电容会向直流线路放电，如图2所示。在整个暂态过程中，故障分量可以分为换流器子模块电容放电部分以及交流馈入部分。由于直流系统对保护检测和动作的速度要求极高，一般要求在几个毫秒内完成，在考虑这么短的时间内的响应时，交流馈入部分的故障分量可以忽略不计[17]。此时，MMC换流器可以等效成一个RLC串联阻抗，如图2所示。其中，Req、Leq、Ceq分别为换流器的等效电阻、等效电感和等效电容，Zconv为换流器等效阻抗。

图2 MMC等值模型

由于双极直流线路正负极之间存在耦合，而极间电压（即线模量）是故障特征最明显的量，故以下故障分析均在解耦后的线模网络中进行。

2.2 区内极间故障特征

直流线路发生区内极间金属性故障时（图1中的f1点），故障点的电压跌为0，可以等效为一个阶跃信号向线路两边传播，在故障点和线路出口处发生折反射。以保护R1为例，根据彼得逊等效法则和叠加定理，可以得出图3所示的故障分量等效电路图。其中，Zconv表示换流器等效阻抗，La表示限流限抗器，Zl表示直流线路波阻抗，uf表示故障点处附加的电压源。

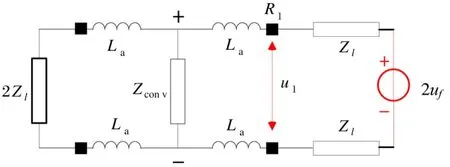
图3 区内极间故障等效电路

区内极间故障下保护R1所对应的传递函数为：

其中，Zin是从R1处看进去的输入阻抗，Zin(s)=2sLa+Zconv(s)∥(2Zl(s)+2sLa)，Zl(s)为频域线模波阻抗，Zconv(s)为换流器等效频域阻抗。

设故障前瞬间极间电压幅值为E，则R1处的测量电压为：

2.3 区外极间故障特征

区外极间故障主要分析反方向换流站母线故障和正方向换流站母线故障，即图1中的f2、f3点，其故障等效网络如图4所示。

图4 区外极间故障等效电路

反方向换流站母线故障时（f2），故障暂态量从母线传到R1处，有传递函数：

正方向换流站母线故障时（f3），故障暂态量先从相邻换流站母线传到线路侧，再经过线路传到R1处，其传递函数为：

同上节，根据传递函数和等效电路图可写出R1处测量电压的表达式，此处省略。

2.4 区内单极接地故障特征

对于架空线路而言，单极接地故障发生率较高。区内单极接地故障下，线模故障网络等效电路图与图3一致。设故障前两极电压对称，幅值均为E/2。当a极（以正极为例）发生单极接地故障时，在故障点处，故障极的电压跌为0，并在非故障极感应出耦合分量，可得故障点处两极的前行波分别为：

其中，Zg和Zl分别为线路地模和线模波阻抗，Rf为过渡电阻。

此时故障等效电压源为：

同理，根据等效电压源以及式（1）可写出末端电压的表达式。

2.5 区内外故障特征对比

根据以上计算公式，选取一组换流器典型参数，并设La=0.1 H，波阻抗为375 Ω，由此得出区内外故障下的线路保护R1所对应的传递函数幅频特性，如图5所示。可见，在高频段（＞1 kHz），区内外故障的传递函数幅值具有明显的区别：区内故障传递函数幅值基本保持为2；区外故障传递函数幅值随频率上升而降低，且远小于2。在区内故障下，传递函数反映的是由限流电抗器及换流器组成的线路边界对故障信号在线路末端的折射情况，由于线路边界对高频信号呈现出的阻抗很高，相当于开路，入射波和反射波的叠加使高频分量被放大。而区外故障下，由于线路边界阻碍了高频量的通过，其高频分量随频率升高而减小。因此，末端电压的高频含量大小是区内外故障特征的主要差异之一。

图5 故障传递函数幅频特性

3 保护原理

3.1 故障检测判据

区内外故障均会导致保护安装点处线模电压的下降，因此可以用极间电压Udc（即线模量）幅值的跌落作为保护启动判据，快速检测故障的发生：

其中，up和un分别为直流线路的正、负极电压，Uset为门槛值，门槛值的选取要躲开系统正常运行时极间电压的最小值。若按直流电网最大电压偏移量为10%的标准计算，Uset可取为0.9倍额定电压。

3.2 区内外故障识别判据

由上节分析可知，由于线路边界的存在，区外故障时保护处测得的故障电压高频能量将很低。而区内故障时虽然故障电压中的高频量较大，但高频量的绝对值会随过渡电阻的增大而减小，因此仅利用高频能量绝对值大小难以可靠识别区内外故障。为此，以低频能量为参照，利用高频段能量的含量大小作为指标将更适合用于区内外故障的判别。

由于小波变换适合于处理非平稳、非周期信号方面，能很好地反映信号突变处的特性[18]。因此，本文利用小波变换对暂态信号进行处理，进而构成识别判据。首先定义暂态电压高、低频能量比值k为：

其中，EH和EL分别为故障电压信号的高频段和低频段小波能量。对离散信号作多层小波分解，第i层信号的小波能量可以表示为：

其中，di为小波变换后第i层的细节系数。

由幅频特性图可以看出，区内外故障幅频特性在低频段的差异较小而在高频段的差异很大，因此k值主要受到高频段能量的影响，区内故障的k值将远大于区外故障下的k值。另外，由于过渡电阻只影响电压幅值而不改变频率特性，故k值受过渡电阻的影响较小。设定区内外故障识别判据：

当满足式(12)时，判定为区内故障。其中，kset的选取要躲开区外故障k值的最大值。

3.3 故障选极判据

由于单极故障下两极电压存在地模量，取其在一段时间内的积分，可以得到地模电压积分值，定义为S。当S的绝对值大于门槛值时，判定为单极接地故障：

其中，up(n)和un(n)分别为正极电压和负极电压在第n个采样点的采样值；n1为满足(8)的第一个采样点；N为积分区间长度；Δ1为门槛值，其选取时要躲开系统正常运行时S的最大值。

发生单极接地故障后，故障极电压下降，非故障极将产生过电压，因此S的正负与非故障极电压极性一致。设定故障选极判据为：

S＞0 （17）

当满足(17)时，判为负极接地故障；反之，判为正极接地故障。

3.4 保护算法

根据以上所述，本文设计了基于小波变换的直流电网线路故障识别方案，其流程图如图6所示。正常运行时，通过检测极间电压幅值判断故障发生，利用小波变换后的高、低频能量比值判别区内外故障，最后利用电压地模量积分值判断故障类型。

图6 保护算法流程图

4 仿真验证

4.1 仿真模型

在PSCAD/EMTDC中搭建了如图1所示的四端直流电网进行仿真测试。直流电网为双极接线方式，接地方式采用直流侧经箝位大电阻接地。系统额定直流电压为±200 kV，额定功率为400 MW。换流器采用九电平MMC模型，子模块电容为3 000 μF，桥臂电感为0.02 H，续流二极管电阻为0.05 Ω。换流站1采用定直流电压控制，换流站2、3和4采用定功率控制。限流电抗器取值为0.1 H。直流线路采用频变参数模型，L12、L14、L23、L24和L34长度分别为300 km、200 km、100 km、150 km和100 km。

本文选取db4小波，保护采样率为10 kHz。取故障前后各1ms的数据作小波变换、取第一层和第三层暂态能量进行判据计算。故障检测判据Uset设为360 kV。式(16)积分区间长度N取5，门槛值Δ1按照电压最大允许偏移量与积分区间长度的乘积计算，本文设为10%，即Δ4=400。

4.2 典型故障仿真

以保护R1为例，设置t=1 s在不同位置（区内0 km、区内300 km、正方向母线和反方向母线）分别发生极间短路和正极接地故障，过渡电阻均为0 Ω，其仿真结果如图7所示。可见，利用单一的门槛值，本文所提的保护原理能准确判别两种故障类型下的区内外故障。考虑一定的裕度，本文把kset取为0.2。在正极接地故障下，地模电压幅值逐渐增大且极性为负，而极间故障下地模电压基本为0，因此故障选极判据能够准确动作。

4.3 过渡电阻的影响

以架空线为传输线的直流电网线路保护需要考虑过渡电阻的影响。由式(6)可知，过渡电阻会使故障等效电压源幅值降低，从而影响末端电压的小波能量计算值。设置直流线路L12在不同位置、不同过渡电阻下发生极间故障、正极接地故障，k值的计算结果如图8所示。可见，本文所提保护原理在区内500 Ω过渡电阻下依然能正确动作，具有很强的耐受过渡电阻能力。

5 结论

以架空线为基础、配置直流断路器与限流电抗器的MMC型系统是目前直流电网的发展趋势之一，其安全运行需要配合可靠的直流线路快速保护原理。本文在分析了直流架空线路故障暂态特征的基础上，根据区内外故障的频率特征差异，提出了基于小波分析的快速保护原理，能实现区内外故障判别以及故障极判别。该保护原理仅需采用单端电压信息，保护时间窗短，动作速度快。仿真结果表明，所提保护原理能有效区分区内外故障并能准确判别故障极；具有较高的耐受过渡电阻能力。