电磁场作用下粒子的运动①

， ,

(佳木斯大学，黑龙江 佳木斯 154007)

0 引 言

电磁场(electromagnetic field)是电磁学的一个重要概念，它是由带电物体产生的一种物理场。电场随时间变化产生磁场，磁场随时间变化产生电场，当物体处在其中时会受到电磁场力的作用[1]。电磁波就是由电磁场以光速向四周传播而引起的，具有能量和动量。物理学家麦克斯韦用了四个方程构成麦克斯韦方程组很好的诠释了电磁场的特征、性质以及场中物质的运动变化所遵循的规律[2-3]。但是粒子在电磁场中的运动是极为复杂的，所以研究带电粒子在电磁场中的运动不仅在物理学领域有着重要意义，而且在材料科学领域以及微电子领域都有着重要的理论意义和实际应用价值。

1 粒子运动的理论分析

1.1 电场中的粒子的运动

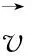
(1)

1.2 磁场中的粒子的运动

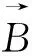
1.3 电磁场中的粒子的运动

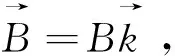
(2)

粒子的运动轨迹为回旋线，回旋是在与磁场垂直的平面内进行。

2 电磁场中粒子运动的应用举例

2.1 真空中电磁场作用下粒子运动的轨迹

虽然带电粒子的轨迹在电磁场的作用下是极其复杂的，但当真正了解和掌握了粒子的空间运动规律，问题就变得简单了，电磁场的作用就可以很好地被应用，下面介绍几个电磁场作用下的粒子运动轨迹实例，同时也是一种美的欣赏[5]。

2.1.1 例1

如图1所示，质量为m，带电量为q的粒子，在外加电场的作用下加速获得一定的能量后进入均匀磁场中，磁场一区磁场强度大小为B,方向为垂直于纸面向里，磁场宽度为a，磁场二区磁场强度大小也为B,方向为垂直于纸面向外，磁场宽度为无限大。

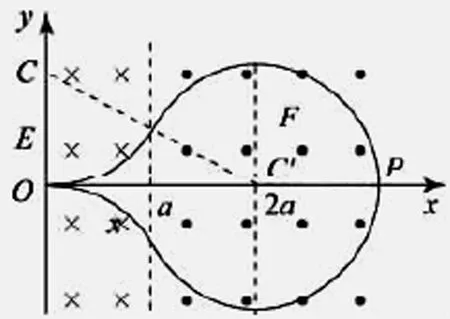
图1 例1图示

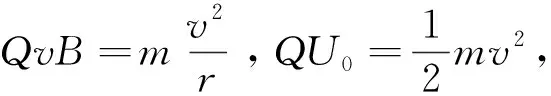
2.1.2 例2

如图2所示，磁场垂直于纸面向里，带正电的小球由P点以初速度v0垂直于MN进入磁场，如果磁场不发生变化，小球将作匀速圆周运动，之所以能形成图示2的具有对称性的曲线，由磁场的基本知识可知，所加的磁场应为周期性变化的磁场，这样在洛伦兹力的作用下就能改变带电粒子的方向，周期性变化的磁场形成了粒子运动的对称性曲线。

2.1.3 例3

如图3形成的8字形曲线和图4吊坠形曲线所示，这样的曲线的形成即在空间存在匀强的电场的同时，CK上半空间施加垂直于纸面向外的磁场强度大小为B的磁场，CK下半空间施加垂直于纸面向里的磁场强度大小为2B的磁场，通过受力分析调节入射的粒子的初速度满足粒子不从NS边飞出即可形成图示的8字形曲线，改变粒子的入射速度保证粒子能经过D点从MT边飞出即形成吊坠形曲线。

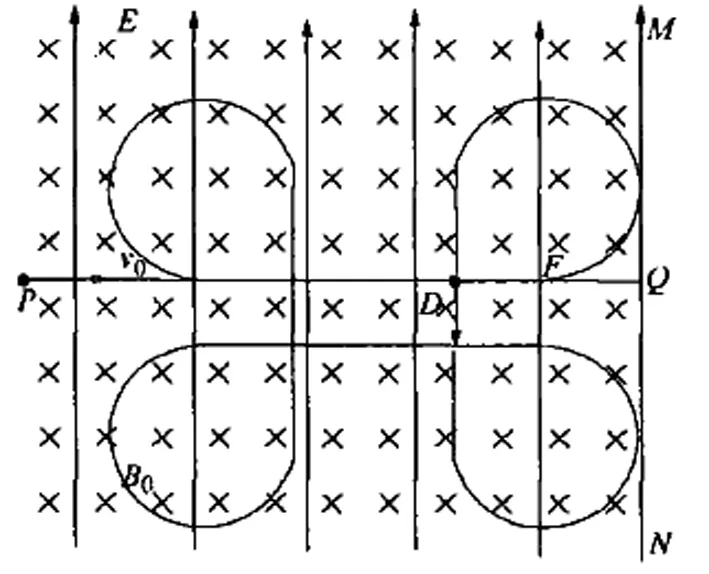
图2 例2图示

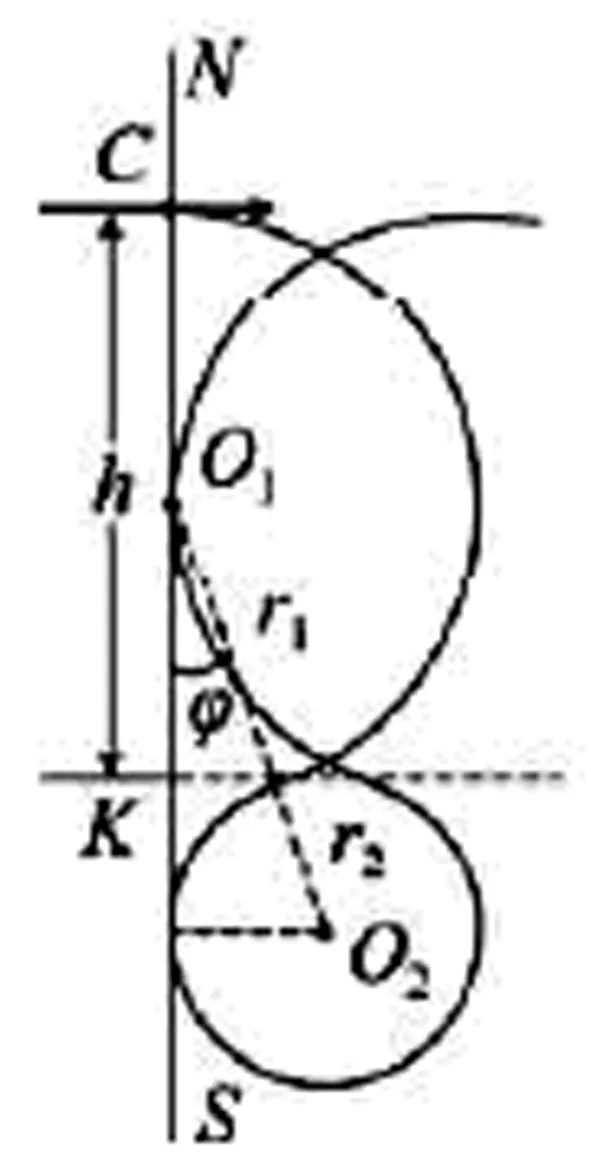
图3 8字形曲线

2.1.4 例4

如图5所示，粒子运动的轨迹像一朵小花，同时具有对称性。形成这样轨迹的条件是轨迹空间充满垂直纸面向里的均匀磁场，但磁场强度随时间作周期性变化，这样复杂的轨迹同样是通过洛伦兹力提供向心力来实现的，只是磁场周期性变化决定了分析的阶段性。

2.2 电介质中电化学沉积下粒子的运动

电化学沉积实际就是利用电泳效应，电解质溶液中存在溶质离子和溶剂分子，它们之间存在着相互作用，影响着离子的电导率，从而完成金属沉积过程，电沉积是重要的材料制备方法，一般金属电沉积过程可分为传质、表面转化、电化学步骤、新相生成等几个环节。

都知道电磁场的能量容易控制，可以通过非接触式的方式对材料施加作用，在不对材料造成污染的同时可传递热能和动能给材料，所以电磁场能提供非常清洁的材料加工技术，材料在电磁场作用下主要受到洛伦兹力和磁化力。

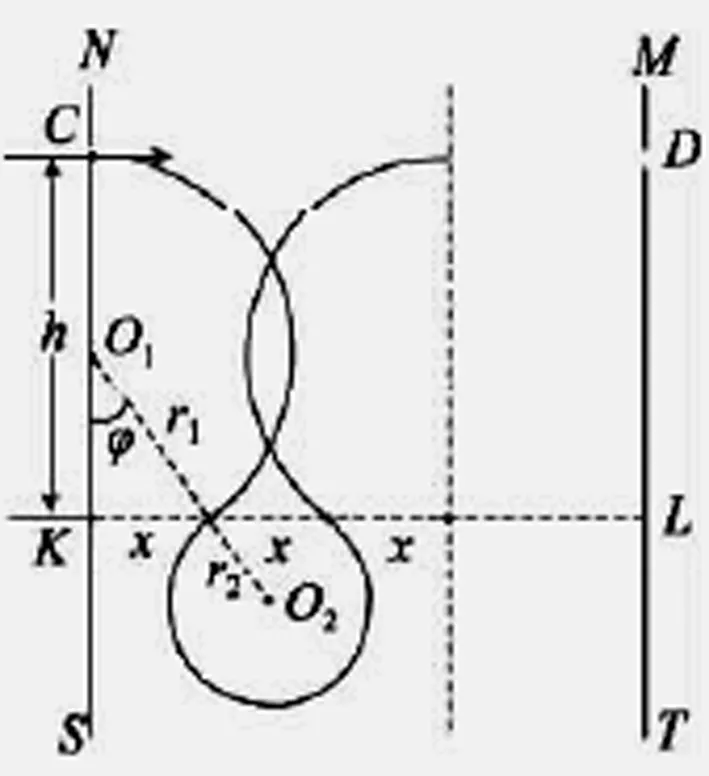
图4 吊坠形曲线

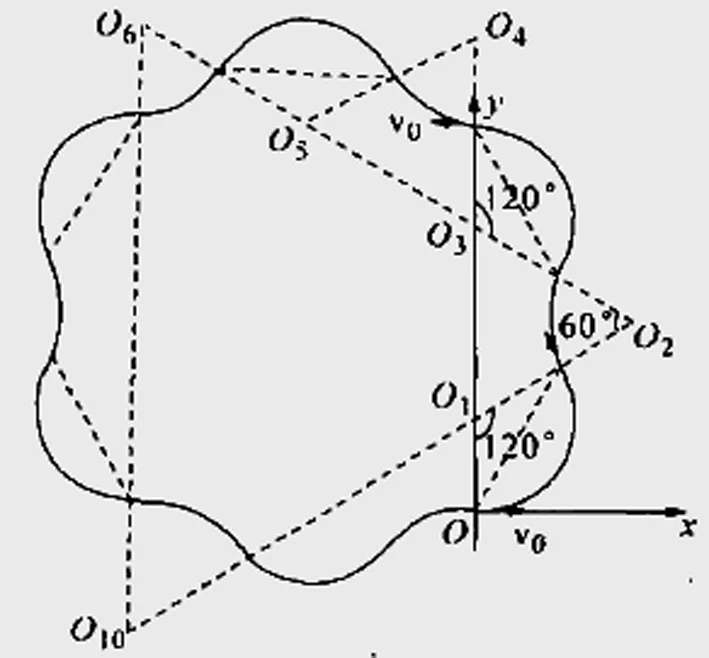
图5 例4图示

大量研究表明磁场的施加会对电镀过程产生影响，其中包括洛伦兹(Lorentz)力所引起的磁流体力学效应(MHD)。MHD的出现增强了带电离子的传输，促进了粒子的成核速度，使电沉积薄膜表面晶粒得到细化，表面变得更加平整，主要因为晶粒的成核速度与生长速度的快慢直接影响到表面形貌，当成核速度加快时，薄膜晶粒细化，表面就平整，当生长速度过快时，晶粒变粗变大，沉积表面变得粗糙[5]。

另外，通过磁场的作用，镀液中离子的水化程度降低的同时镀液的电阻率也随之降低，这样镀液的分散能力提高。结合电磁场中的毕奥—萨伐尔定律

(3)

和电导率与扩散系数之间的关系

(4)

知道离子的运动速度越快，扩散系数越大，镀液的导电能力也会增强，电导率增大。如图6和图7所示[6]施加电场后沉积的金属粒子更加均匀并且晶粒细化，由于磁场施加方向与电极表面垂直，这样金属离子在沉积过程中因为切割磁力线受到洛伦兹力的作用，改变了运动轨迹在粒子周围发生旋涡，促进了电极附近的介质传输，增强了带电离子的传输，降低了阴极表面的浓度差，减薄了扩散层，使电沉积在较高的过电位下进行的结果。

图6 无磁场作用的电沉积

图7 施加磁场的电沉积

3 结 语

粒子在电磁场中的运动既简单又复杂，简单是在电场和磁场中分别受到库仑力和洛伦兹力，只要按着牛顿运动定律进行受力分析，由动力学方程向运动学方程的转变过程，复杂的是当电场和磁场同时作用于粒子，并且场的大小和方向都在发生改变，这时粒子的轨迹就变得复杂，但是无论情况如何，只要把握好电磁场作用时的基本规律，做出正确的分析，电磁场的能量就会被很好地利用。