基于引力搜索算法的动车组端门自动控制技术①

, ，

(1. 中车长春轨道客车股份有限公司,国家轨道客车工程研究中心，吉林 长春 130000；2. 吉林大学仪器科学与电气工程学院，吉林 长春 130000)

0 引 言

高速动车组已成为人们出行的最主要的交通工具之一，在人们的生产和生活中正扮演着越来越重要的角色[1]。与传统的轨道客车相比，高速动车组不但在运行速度上大幅提升，而且在电气化、自动化及智能化等方面的要求也越来越高[2]。端门是高速动车组车厢与车厢之间的连接门，是乘客进出车厢的通道，是乘客使用频率最高的部件之一。因此，端门运行的可靠性及安全性等性能与旅客的人身和财物安全息息相关。针对高速动车组自动端门运行性能要求以及高振动和强电磁干扰的运行环境，提出一种基于引力搜索算法的动车组自动端门优化控制方法，实现自动端门的优化控制。

1 自动端门系统工作原理

高速动车组自动端门由有刷直流电动机提供门体运行动力，电动机旋转经过传动机构带动门体进行开启和关闭运动，检测装置——光电编码器监测门体的运行位置和速度(如图1所示)。

直流电动机是自动端门系统的动力源，因此通过对直流电动机旋转的优化控制，即可实现对自动端门运行过程的优化控制。系统采用全桥式双极性驱动电路实现电动机的驱动控制，通过优化调整加载在电动机电枢上的电压实现对自动门运行方向和速度的优化控制。如图2所示。

图1 自动端门系统组成

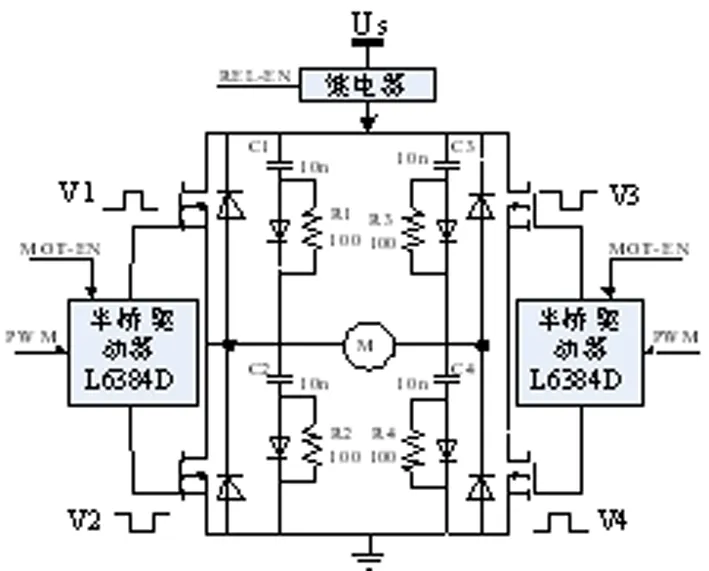
图2 全桥式双极性驱动原理

2 控制模型建立

直流有刷电动机是自动端门系统的动力源，是系统直接优化控制对象，通过对电动机的优化控制实现对端门运行过程的优化控制。

直流电动机的输出转速可以描述为

(1)

式中，n为电动机转速；U为电动机供电电压；R为电枢回路电阻；Φ气隙磁通量；I电枢回路总电流；Ce电动势常数。

由于系统采用全桥式双极性驱动电路实现直流电动机的驱动控制，因此加载在电动机电枢上的电压可表示为

(2)

式中，US为供电电压；T为PWM周期；t1为PWM周期内正电压输出时间；α为输入电压占空比。

根据式(2)可知，通过调整占空比α实现对加载在电动机电枢上的电压U的调整，实现对直流电动机转速的优化控制。

根据式(1)、(2)可得电动机转速与输入电压间的表达式

(3)

直流电动机通电后，电枢绕组流过电流，载流导体在磁场中受力产生电磁转矩，在电磁转矩作用下电动机旋转拖动传动机构做工。门体运动所需转矩Tout主要需要克服电动机空载输出转矩Towto0、门体运行运动阻力转矩Tout1和端门水平运动折算的转矩Tout2，可描述为

Tout=Tout0+Tout1+Tout2

(4)

电动机额定输出转矩Tout0可表示为

(5)

式中，P电动机额定功率；n0电动机额定转速；

i减速机减速比。

克服运动阻力F的输出转矩Tout1可表示为

(6)

式中，V为门体运行速度；nout为电动机输出转速；η为传动机构传动效率。

假设端门门体质量为m，端门运动折算到电动机的输出转矩Tout2可表示为

(7)

通过上述分析可知直流电动机输出转矩Tout可表示为

(8)

直流电动机的电磁转矩T可利用电磁转矩常数CT表示为

T=CTΦI

(9)

将式(9)代入式(3)可得直流电动机的转速特性方程

(10)

文中所说的电动机包含减速机，假设电动机与减速机间传动无效率损失，设减速机的减速比为i，减速机输出转速nout和输出转矩Tout可表示为

nout=in

(11)

(12)

综合式(9)、(10)、(11)和(12)可得系统传递函数模型

(13)

式中，

根据式(13)可知，电源电压、运动阻力、门体质量和运动加速度是影响电机转速的主要因素，通过调整电源电压的占空比来对电机转速进行控制。

3 自动端门优化控制技术

通过前面的分析可知，直流电动机的转速，即门体的运行速度，与电源电压Us、门体运行阻力F和门体质量m及门体行进的加速度dn/dt等参变量有关。由于高速动车组运行过程中，供电电源电压、门体运行阻力及门体质量等差异和外界干扰因素不可避免，拟通过基于引力搜索算法的优化控制算法实现对自动端门的优化控制。

直流电动机数字调速系统通常采用增量PID控制算法，由于增量PID算法的采样周期非常小，差分对数据误差和噪声特别敏感，一旦出现干扰，差分会突然变大，从而引起控制量的病态增大[3]。而自动端门运行过程中外界干扰不可避免，因此为了有效地抑制干扰对自动端门系统运行过程中产生的扰动，在增量PID算法的基础上加入了低通环节，构建不完全微分PID算式，并通过引力搜索优化求取PID参数，实现对电机的优化控制。

不完全微分的PID增量算式为：

ΔuD(k)=KP[e(k)-e(k-1)]+KIe(k)+

KD[e(k)-2e(k-1)+e(k-2)]+

αΔuD(k-1)

(14)

式中，Kp为比例系数；KI为积分系数；KD为微分系数；e(k)为第k次采样时刻的偏差值；e(k-1)为第k-1次采样时刻的偏差值。

引力搜索算法是一种基于牛顿万有引力法则的启发式搜索算法[4 ]。在牛顿万有引力中，两个粒子之间的引力正比于其质量的乘积，反比于它们距离的平方。这些粒子彼此通过引力拉扯对方，这个力使粒子整体向质量大的粒子移动。在引力搜索算法中，每个粒子有四个特征：位置、惯性质量、主动引力质量和被动引力质量，一个粒子的位置等于一个解决问题的方案[5 ]。

基于引力搜索算法的PID优化控制算法结构如图3所示。PID参数Kp、KI、KD通过引力搜索算法确定。

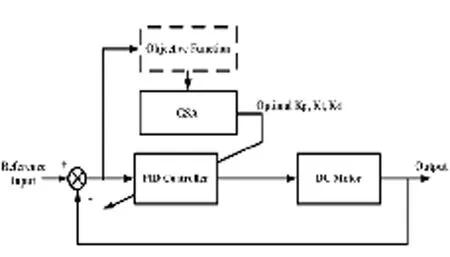
图3

图4 实验装置

基于引力搜索算法的PID参数计算方法如下：

(1) 初始化

系统取30个粒子，3个维度即Kp、KI、KD三个PID参数，每个粒子的位置是随机的。那么第i个粒子可表示为

(15)

其中，xi2是第i个粒子在第2个维度的位置。

(2)评估所有粒子

在每一次循环中处理所有粒子，并且最好的、最坏的适应度在每次循环中描述为

(16)

(17)

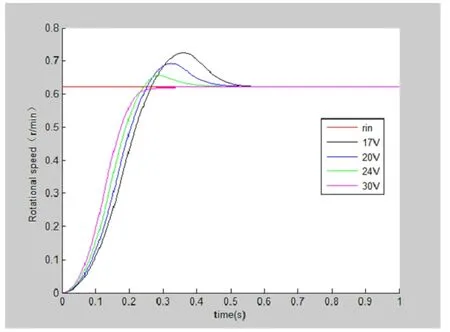
图5 开门过程速度曲线

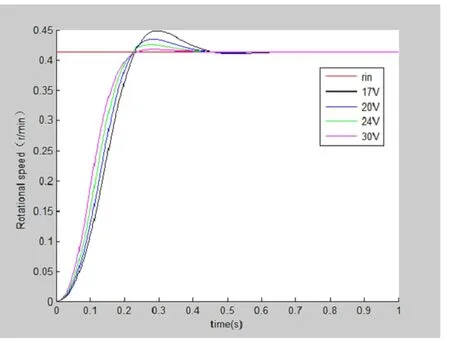
图6 关门过程速度曲线

其中，fitj(t)是第t次循环中第j个粒子的适应度，best(t)和worst(t)分别是第t次循环中所有粒子中最好、最坏的适应度。

适应度函数fitj(t)为

(18)

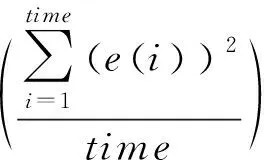
(3) 计算引力常数G(t)

第t次迭代的引力常数G(t)为

(19)

其中，100是引力常量的初始值，20是自主选取的一个常数，t是当前迭代次数，200是总迭代次数。

(4)更新引力和惯性质量

每个粒子的引力和惯性质量在每次迭代中更新为

Mai=Mpi=Mii=Mi,i=1,2,...,30

(20)

(21)

其中，Mai第i个粒子的主动引力质量；Mpi第i个粒子的被动引力质量；Mii第i个粒子的惯性质量；Mi(t) 第t个迭代里第i个粒子的质量；fiti(t) 第t次循环第i个粒子的适应度，式(21)可以表示为

(22)

(5)计算总力

第i个粒子受到的力的总和：

(23)

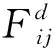
(24)

其中，Rij(t)为第i个和第j个粒子间的欧几里得距离‖Xi(t),Xj(t)‖2；ε为很小的常数。

(6) 计算速度和加速度

第d维度循环t中第i个粒子的速度(vid(t))和加速度(aid(t))通过万有引力定律和运动定律计算

(25)

(26)

其中，randi为区间[0,1]上的一个随机数。

(7)更新粒子的位置

第d个维度第i个粒子的位置更新为

(27)

(8) 重复(2)到(7)步会一直重复直到迭代次数达到标准。在最后一次迭代中，算法返还规定维度对应粒子的位置值。这个值也是最优问题的全局解。

4 实验与数据分析

为验证所优化控制算法的可行性和性能，采用如图4所示的装置进行实验。系统中直流电动机主要性能参数：标称电压DC24V，额定电流4.5A，额定功率100W，额定转速3350r/min，减速比1:10，传动齿轮分度圆直径105mm，门页质量50kg。

通过在系统电源电压为17V、20V、24V、30V下对自动端门的开、关速度进行测试，获得的速度曲线如图5、图6所示。

开门速度约为205mm/s，关门速度约为139mm/s，能够满足动车组自动端门对开门速度的控制要求。开门速度上升时间tr小于0.18s，超调量σ% 小于16.13%。关门速度上升时间tr小于0.15s，超调量σ%小于9.76%。测试结果表明，系统具有良好的动态性能，能够满足自动端门实际运行控制要求。

5 结 论

建立了自动端门系统的控制模型，在不完全微分增量PID算式基础上通过引力搜索优化算法实现自动端开启和关闭运行过程的优化控制，最后通过实验证明所提出的优化控制方法具有较好的效果，能够满足高速动车组电动端门的优化控制要求。