考虑电动汽车随机到达的光储微电网能量管理模型

王锐，姚兴懿，李文桦

（国防科技大学系统工程学院，湖南 长沙 410072）

引言

随着经济社会不断发展，人们对分布式可再生能源的发展与应用需求越来越高。微电网是利用分布式可再生能源的有效形式，其经济稳定运行需要有效的调度策略，因此需要通过对微电网能量管理模型的寻优，找到最佳的控制策略[1]。电动汽车作为使用清洁能源的代表，得到了国家的大力支持[2]，随着电动汽车的普及，也对原有不考虑电动汽车接入的微电网模型提出了新的要求[1]。电动汽车作为可变的灵活负载，既能简单的作为一种负载，又能将其归类为灵活的储能设备。由于电动汽车使用清洁能源，所以在降低二氧化碳排放、缓解能源危机上具有重要作用[3-4]。在电动汽车市场占有量越来越大和国家推进能源互联网发展的背景下，智能的电动汽车充电场应运而生。

文献[5]研究了电动汽车充电对电网的影响，提出用户充电时间和空间上的随机性将增加电网运行的不确定影响因素；文献[6]利用随机规划对家用电动汽车随机充电作了研究，但是考虑到随机规划对其研究目标的概率要求掌握较高，而实际中一般难以得到准确概率，实际效果将打折扣；文献[7]指出，如果电动汽车随机接入电网并无序充电，则即使是高渗透率的电动汽车也会对电网造成巨大冲击；文献[8]通过构建微电网个体的详细仿真模型，研究含充电桩的微电网协调控制策略，通过对控制策略的有效性进行检验，发现控制策略因预测不准而实际效果不好；文献[9]通过建立单体电动汽车充电模型研究了电动汽车充电负荷时空分布对电网的影响，但未涉及充电站优化问题；鲁棒优化模型考虑系统最差情况下的求解，对实际指导有积极作用，越来越受到重视[10-11]。在优化调度策略的求解方法上，传统的调度方法存在许多问题，日前调度方法由于需要准确的预测数据，对波动性较大的场景调度策略存在较大问题；文献[12]使用模型预测控制方法，充分考虑了实际不确定因素，取得了较好的实际应用效果，但是没有考虑到实时功率调整对大电网带来的冲击。

本文采取日前调度与模型预测控制相结合的优化调度策略，对微电网系统中的不确定性因素，利用鲁棒优化方法，建立了考虑电动汽车充电场所的微电网能量管理模型，引入分时电价和电价惩罚因子减轻电网负担，利用CPLEX软件对该模型进行求解，为优化充电提供决策支持。

1 模型

本文研究的模型包含典型的微电网模型以及电动汽车的随机到达模型。其包含多个充电桩、高渗透率的可再生能源电源、储能设备和系统负载。由于微电网优化调度模型涉及参数较多，特在此将相关参数归纳如下：

参数 参数 含义类型Psolar(k)光伏预测输出Pload(k)负载预测输出Ebess(k)储能系统的容量水平预buysell测cgrid(k)， cgrid(k) 大电网的买入和卖出单价变量Tarrive，Tleave电动汽车的到达和离开时间EV,jEV,j Pˆload(k)负载变化范围Pˆsolar(k)负载变化范围δbcess(k )储能系统充电状态，二进制变量δd(k )储能系统放电状态，二进制bess变量Pbcess(k)储能系统充电功率Pbdess(k)储能系统放电功率δginrid(k)， 与上级电网交互状态，二进δgoruitd(k)制变量Pgin rid(k)，决Pout(k)与上级电网交互功率策grid变δ(k )充电桩接入状态，二进制变量EV, i量δP, i(k )充电桩充电状态，二进制变量PEV, i(k)电动汽车充电功率EEleVav, ej 实际离开时刻电量zbalance(k)pbalance,1(k)功率平衡约束辅助决策变p(k)量，二进制变量balance,2 Γ(k )鲁棒模型的调整量，balanceΓ balance(k)∈[0,1]Cbess(k)储能系统运行维护成本费Cgrid(k)与大电网的交互成本用Cpunish(k)超出交互计划的惩罚费用grid Cpunish电量未充满带来的惩罚费用EV

1.1 基本模型

1.1.1 电动汽车模型

在任意时刻，电动汽车到达及离开为随机过程，其到达离开的概率可根据历史数据总结并进行预测。在预测时间段内，某一时刻电动汽车到达离开可近似看成泊松分布，即任意时刻电动汽车到达数量的概率如下：

式中λ(t)为随时间变化的量，N为t时刻最大车辆到达量。

由于景区的特殊性，用户停留时间与目的地价格水平、目的地旅游服务质量、高等级旅游景区数量、游览景区数量、旅游方式、行程安排、交通价格、空闲时间、客源地与目的地距离等有关[14]。同时，统计数据显示，停留时间与游客到达景区的时间具有很强的相关性，例如早上八点以前到达的游客很大可能中午离开，而下午到达的游客则可能次日离开。在剩余电量方面，可以假设其剩余电量小于80%电池容量[15]。一般而言，用户只有当电量不足时才会选择进入充电场所而非停车场。基于统计数据及游客的到达离开泊松分布模型，本文利用蒙特卡洛方法（Monte Carlo method）[16]产生一系列电动汽车到达时间、离开时间和剩余电量数据对模型进行求解。

电动汽车作为灵活接入负载，主要考虑其充电的时间以及电量约束。其中NEV表示电动汽车数量；δEV,i表示电动汽车接入充电桩状态，为1表示接入充电桩，为0表示未接入；表示电动汽车的充电状态，为1时表示当前时刻正在充电，为0时表示为不充电；ηEV电动汽车储能设备充电效率；εEV和∆t分别表示电动汽车储能设备的自放电能量损耗及每一周期时间长度；分别表示到达和离开的时间。

未到达预计电量的惩罚费用：

约束条件：

公式(3)表示当前接入充电桩的电动汽车数量应该小于现有充电桩数量；公式(4,5)表明电动汽车到达后离开前为接入状态，其余时段为未接入状态；公式(6)保证充电只能在接入充电桩之后才可以进行；公式(7)为充电桩充电功率约束；公式(8)为充电能量的动态约束。

1.1.2 储能系统

作为微电网中最灵活的可直接控制的设备之一，储能系统的地位十分独特，既可以作为用电端设备消纳多余的电能，又可以在发电不足的时候作为备用电源为系统供电，其主要约束包含了储能系统的最大最小容量限制、最大充放电限制、充放电能量转移。储能充电最小、最大功率限制；储能放电最小、最大功率限制；储能最小、最大容量限制；、ηbdess储能充电和放电效率；δbcess、δbdess储能充电、放电状态；εbess和∆t分别表示储能系统的自放电能量损耗及每一周期时间长度。

储能系统运行维护成本和充放电转换成本：

约束条件：

公式(12-15)分别是储能系统的充电功率、放电功率约束、能量水平约束和动态能量转移约束；公式(16)表明储能系统在运行过程中充放电不能同时进行。

1.1.3 与大电网交互模型

随着经济社会发展，微电网与大电网的交互也逐渐增强。对于供电方，未来的发电计划需要提前制定，避免少发电造成不够用或多发电浪费的情况。对于稳定供电的需求，本文将提前一天的购电计划通过日前规划得出，在次日的运行中，引入惩罚成本使得系统与大电网的交互按照购电计划进行，从而减缓大电网的压力。

费用成本：

(1)交互成本

Cgrid(k)表示与大电网的交互成本，和表示与大电网的买入和卖出单价，则成本可表示为：

(2)惩罚费用

结合风、光、负载预测，我们根据日前规划方法，制定第二天的买卖电计划，即得到了与电网的计划交互功率，用表示。定义为超出计划的惩罚系数（与当前电价成比例），则惩罚费用表示如下：

约束条件：

公式(19-20)为与大电网交互的功率约束，公式(21)约束了任意时刻充电与放电不能同时进行。

1.1.4 功率平衡约束

微电网的经济调度的前提是微电网系统能够时刻保持稳定、可靠运行，而这就需要微电网能够时刻保证系统内部供需时刻保持平衡。即：

1.2 目标函数

微电网优化调度问题根据调度的目标不同而有不同的形式和不同的调度方案，例如，经济型调度主要考虑经济目标，环境效益调度主要考虑对环境的影响，安全调度则考虑系统的安全性与充裕性。在这里主要考虑微电网运行的经济性目标。

微电网优化调度的总成本可以表示为：

2 基于模型预测控制与日前调度相结合的鲁棒优化控制模型

2.1 鲁棒优化模型

鲁棒优化理论是指在解决实际问题之前，先将所有可能的不确定因素划归在一个固定的集合中，通过鲁棒优化方法产生的最优解能够抑制集合中的任意元素可能造成的不良影响，即优化决策能够应对“最坏的情况”。本文采用D. Bertsimas等提出的鲁棒优化方法[17]。考虑如下形式的线性规划问题：

其中，目标函数cj与系数矩阵aij都是确定性的参数，常数项存在不确定性。假设对于任意有

在式(25)中，τi为参数中所包含的不确定性参数的集合，且对每个不确定参数满足，bis为均值，为参数最大变化幅度。

根据文献[17]提出的鲁棒优化方法，将式(24)等价转化为如下鲁棒形式：

我们对原模型的不确定参数有如下定义：

将式(27)修改为鲁棒对应形式：

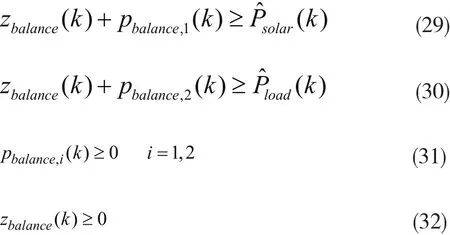
则修改后的鲁棒优化模型描述如下：

目标函数：

约束：

2.2 模型预测控制与日前调度相结合

传统的调度策略虽然能够在一定程度上对系统运行做出合理的控制策略，但是其存在许多弊端。实时调度不考虑未来时段的调度，只需要满足当前的功率平衡约束，运行费用较高；日前调度根据预测数据，如光伏发电功率、用户负载等，规划未来一段时间的调度计划（通常是一天），但由于预测数据和实际数据不完全一致，特别是电动汽车到达和离开时间预测较为困难，因此实际运行过程中，日前调度将会产生过高的交互惩罚费用。

模型预测控制将规划未来一段时间的运行策略，并执行当前时刻的决策。下一时刻，继续规划未来一段时间，并执行。其在满足功率平衡的约束下，对预测数据的不稳定性处理较好。

本文采用模型预测控制与日前调度相结合的方法进行优化控制。先通过日前调度方法对未来一天内各设备运行进行规划，得出微电网与大电网交互计划，并提交给电能提供方。电能提供方将通过用户提交的用电计划大致决定第二天的发电计划和供电计划。实际运行时，首先规划当前时刻到规划结束时刻的系统运行策略，并执行当前时刻的策略；到达下一时刻时，继续规划当前时刻到结束时刻的策略，然后执行当前时刻规划；如此进行滚动规划，直到到达规划结束时刻。其优化过程如图1所示：

图1 模型求解步骤Fig.1 Model solving steps

3 案例分析

3.1 案例描述

本文选取重庆某景区微电网示范项目作为研究对象，其简化模型如下图所示：

图2 重庆某景区微电网示意图Fig.2 A scenic of Chongqing micro-grid diagram

该景区微电网与外界电网连通，系统包含储能系统(可控制是否接入)、光伏发电设备、公共负载和公共充电桩。景区提供的充电桩共有15个，可为游客的电动汽车提供充电服务，其最大可提供的充电功率为7kW，充电效率为95%，能量自损耗为0.02kW。储能设备最大储能容量为70kWh，充放电效率为95%，储能系统自放电能量损耗0.02kW,最大交互功率80kW。电动汽车数据取自电动汽车时代网，型号为比亚迪E6，具体参数如下：

表2 电动汽车性能数据Tab.2 Electric vehicle performance data

光伏发电在同纬度同气候地区具有较高的相似性，算例使用的光伏发电功率和负载功率预测数据来自Global Energy Forecasting Competition 2014[18]，具体数据如图3和图4所示。

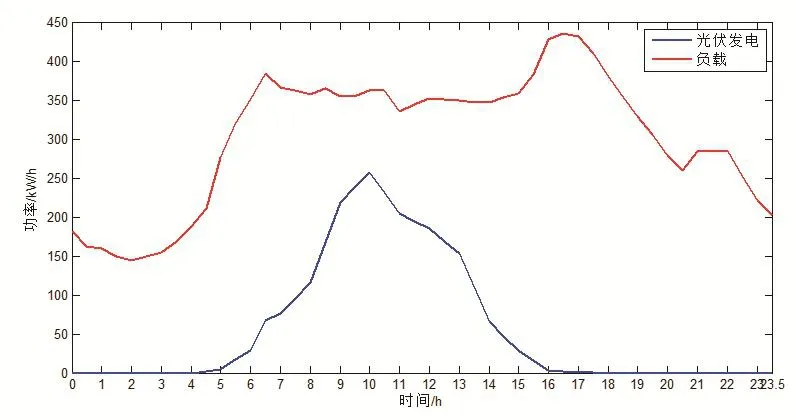
图3 光伏发电及负载预测Fig.3 Photovoltaic power generation and load forecasting

图4 一日分时电价示意图Fig.4 Time-of-day electricity price diagram

由于本文没有景区的电动汽车历史到达数据和离开数据，因此在使用蒙特卡洛方法产生电动汽车到达及离开时间数据时，使用了景区一天内游客的到达时间分布，并按照比例缩小规模，其一天内具体时刻到达数量的均值如图5所示：

图5 电动汽车到达离开时间分布Fig.5 Electric car arrival and departure time distribution

3.2 实验结果

实验相关参数设置如下：

表3 实验参数设置Tab.3 Setting of experimental parameters

(1)车辆随机到达与均匀到达对比

电动汽车充电站对电动汽车到达即离开时间较为敏感，不同的电动汽车到达离开时间模型将对微电网运行及调度策略产生巨大影响。本文以重庆某景区的电动汽车充电站为案例进行研究，充电用户具有停留时间长、到达离开时间不定等特点。基于历史数据指的是在日前调度阶段，根据电动汽车历史到达离开记录（图5）对第二天电动车到达和离开进行预测，并根据预测数据规划第二天与电网的交互计划；完全均匀到达指的是在日前调度阶段，各时刻电动汽车到达离开是完全随机的。针对景区用户特点，本文研究了不同电动汽车到达离开模型下的微电网运行特性，具体过程为：首先通过蒙特卡洛方法分别基于历史数据和完全均匀随机产生第二天电动汽车到达及离开的时间，接着根据对第二天的预测数据产生与电网的交互计划。在第二天的实际运行过程中，根据当天的电动汽车实际到达情况实时调整。为消除由于电动汽车充电量的不一致对结果造成影响，统一将电动汽车一天内到达数量设置为50辆，且总需求电量一致，其结果如表4和图6所示：

表4 运行数据对比Tab.4 Operating data comparison

图6 电网交互及充电功率对比Fig.6 Grid interactive and charging power comparison

从表4和图6可以看出，基于历史数据相较于完全均匀到达，在微电网实际运行过程中超出交互计划的惩罚费用低，并且用户满意度较高。这是因为，基于完全均匀到达而规划的与大电网的交互计划与实际情况相差较大。在实际过程中，由于电动汽车停留时间绝大部分在白天(早8点到晚8点)，夜晚基本没有，所以电网交互的惩罚费用在均匀规划时非常大。同时，系统在实际运行中，考虑到与电网交互的惩罚费用，将限制一部分电动汽车的充电需求，使得电动汽车充电电量不能到达预期，用户满意度大大降低。该对比体现出准确预测电动汽车到达以及离开时间对微电网决策具有重大意义。不准确的预测使得实际与电网的交互与计划交互有较大出入，这将增大电网运行负担，带来运行的不稳定；同时，为了降低不准确预测带来的交互惩罚费用，电动汽车充电也将受到影响，不能被充分满足，用户满意度大大降低。

(2)电价惩罚因子对电网交互的影响

本文在电网交互模型中设置了电价惩罚因子，具体作用是将用户规划的购电计划与当天实际购电相匹配，使供电方供电稳定。式(18)定义了电网交互的惩罚费用，当电价惩罚因子增大时，计划功率交互与实际功率交互差值带来的影响增大，目标函数中电网交互惩罚费用增大。微电网在模型预测控制时，为使惩罚费用降低，会将实际与电网交互的功率与计划购电功率相匹配。在本阶段的实验中，固定鲁棒优化量以及预测数据不确定度，使用基于历史的数据预测电动汽车到达和离开的时间，将电价惩罚因子由0开始变化到1，研究电价惩罚因子对电网交互的影响。定义功率差值如下：

功率差值表示实际运行过程中与电网交互的功率与计划交互功率的差值。

图7 电价惩罚因子对功率差的影响Fig.7 Effect of Price Penalty on Power Difference

图8 电价惩罚因子对交互功率的影响Fig.8 Impact of Price Punishment Factors on Interaction Power

由图7可以看出，随着电价惩罚因子的增大，用户实际用电将会越来越接近其规划用电。实际运行时，因为预测数据与实际数据不一致，功率差不能降低至0，故惩罚因子不能无限增大，在惩罚因子大于0.3以后，继续增大惩罚因子带来的功率差降低效应没有显著提升，惩罚因子大于0.7以后，惩罚因子对功率差值的影响效果变得更差。实际中，一般取惩罚因子为0.2～0.5之间的值。图8显示了计划电网交互功率与实际电网交互功率的对比。计划电网交互根据预测数据对第二天运行进行规划，产生与电网的交互计划（图8红线），实际功率交互为系统根据实际情况功率调整的结果。从图8可以看出，惩罚因子为0时，微电网将不考虑交互计划，故实际运行的功率交互与计划交互有较大的不同，当惩罚因子为1时计划与实际的交互功率基本一致。

(3)充电桩数量及充电功率对用户满意度的影响

在电动汽车模型中，我们引入CEVpunish作为用户电动汽车未到达预定电量带来的惩罚，惩罚费用一定程度上反映了用户的满意度，费用越高，满意度越低。在实际的优化过程中，由于充电桩数量有限，当充电桩被占用时，用户将直接选择离开，这给用户带来了极大的不方便。为研究充电站充电桩数量以及充电功率对用户满意度的影响，本阶段实验中，固定其他变量，分别改变充电桩数量和充电功率大小，采用上文提到的日前调度与模型预测控制相结合的方法，研究其对用户满意度的影响，具体结果如下。

图9表示充电桩数量的设置以及充电桩充电功率对用户满意度影响。由图可以看出，在充电桩数量大于24或者充电功率大于6 kW以后，继续增大相应指标，用户满意度并没有得到显著的提升。进一步研究发现，由于本次实验用到的电动汽车数量为每天50辆左右，当充电桩数量达到一定值时(本文结果为24个充电桩)，充电场能够满足每天的充电需求，用户满意度提高效果较为微小。而本次实验所用电动汽车电池容量为57kWh，可以预见，当充电功率达到饱和时，再通过提高充电功率来获取更高的用户满意度效果不明显。图10表示充电桩数量及充电功率对可充电的电动汽车数量的影响，可以明显看出，充电桩数量越大，则可充电的电动汽车数量也越大；充电桩数量到达30时达到饱和状态。

图9 充电桩数量及充电功率对充电电量的影响Fig.9 Effect of Charging Pile Number and Charging Power on Charging Capacity

图10 充电桩数量及充电功率对充电数量的影响Fig.10 Charging pile number and charging power on the number of charging

4 结语

在微电网中引入可再生能源和储能设备，例如风光发电等，能够进一步缓解大电网的压力。电动汽车作为利用新能源的工具，对节能减排、促进用电结构升级具有积极意义。研究带有电动汽车的微电网问题具有现实意义。

本文考虑了电动汽车的到达及离开模型，根据光伏发电以及对负载的预测，构建了包含充电场所的微电网模型，然后使用鲁棒优化的方法对模型进行了优化。在优化调度策略上，使用日前调度与模型预测控制相结合的方法，能够充分考虑到计划购电与预测数据不准确之间的矛盾。通过对重庆某景区的案例分析，该模型对实际场景下的问题能够得到较为满意的调度策略。如何对大型充电场进行建模以及模型的优化求解方法，将是下一步的研究工作。