磁性斯格明子的研究现状和展望∗

刘艺舟 臧佳栋

1)(中国科学院物理研究所,北京 100190)

2)(新罕布什尔大学物理系,美国 03824)

3)(加利福尼亚大学河滨分校电气及计算机工程系,美国 92521)

磁性斯格明子是具有拓扑保护性质的纳米尺度涡旋磁结构.斯格明子主要存在于非中心对称的手性磁性材料以及界面镜面对称性破缺的磁性薄膜材料中.因具有实空间的非平庸拓扑性,磁性斯格明子展现出丰富新奇的物理学特性,例如拓扑霍尔效应,新兴电磁动力学等,为研究拓扑自旋电子学提供了新的平台.另一方面,由于其具有尺寸小,高稳定性和易操控的特性,磁性斯格明子在未来高密度,低能耗,非易失性计算和存储器件中也具有潜在应用.现阶段的研究已经初步发现一系列磁斯格明子材料,并证明能够通过电流操控室温下稳定的磁性斯格明子,但是室温下单个斯格明子的精确产生、湮灭以及探测在实验上仍具有挑战性.本文阐述了磁性斯格明子的基础理论以及动力学研究现状,并对现有的斯格明子材料和斯格明子的产生,湮灭以及探测方法进行了总结,最后还对未来磁性斯格明子的物理理论研究以及应用发展中的挑战和机遇进行了讨论.

1 引 言

长久以来,几何语言精确地刻画着我们的物理世界.从力的向量表示到引力场的曲率描述,几何获得了巨大的成功.但是近些年在凝聚态物理的发展中,拓扑逐渐受到关注.眼花缭乱的拓扑现象在各类材料中显现,诸如贝里相位、量子霍尔效应、拓扑绝缘体、反常霍尔效应[1−5],以及本文介绍的磁斯格明子[6−8],都是由拓扑保护的.拓扑不仅深化了我们对基础物理的理解,也驱动了技术的革新.磁斯格明子的拓扑稳定性就在驱动着下一代的非易失性存储器件的发展[9].

在几何的语言中,线段是有长度的,物体是有形状的,所以形状、长度不同的物体是完全不同的.而在拓扑的语言中,只要两个物体或物态能够通过连续变形相互转化,就认为它们是等价的.一个典型的例子就是一个马克杯和一个甜甜圈是拓扑等价的,虽然两者完全不同,但是它们都有且仅有一个孔洞,一个马克杯因此可以连续形变为一个甜甜圈.而一个球体由于没有孔洞,所以与上述两者是拓扑不等价的.

磁性系统给出了一个实现不同拓扑构型的平台.根据系统维度和自旋取向空间的不同,磁性体系呈现出了磁畴壁、磁涡旋、磁单极子[10−12]以及磁斯格明子等不同的拓扑构型,从数学上这些构型全都能够用同伦群来描述[13,14].其中磁斯格明子是一种新型的二维拓扑构型.如图1所示,每一个斯格明子的中心自旋和周围自旋指向面外并成反平行,其余的自旋则在面内打转.空间的任何指向都有自旋与之平行,正是由于这个原因,斯格明子态不能连续变形到铁磁态.如果把铁磁态认为是拓扑平庸态的话,斯格明子就是一个非平庸的拓扑态.由于自旋在空间反演下是不变的,磁斯格明子很明显破坏了空间反演对称性,只有在没有反演对称性的磁性材料中才能实现斯格明子的基态.在这类材料里,有一类反对称的自旋相互作用:Dzyaloshinskii-Moriya(DM)相互作用[15,16].正是它和铁磁海森伯相互作用诱导出了斯格明子基态.

基于DM相互作用的斯格明子模型在20世纪80年代就由Bogdanov和Yablonskii[7]提出,但是实验的证明观测直到2009年由德国慕尼黑工业大学的Pfleiderer研究组[17]偶然地利用小角度中子散射(small angle neutron scattering,SANS)在MnSi单晶体中实现.不久之后,日本东京大学的十倉好紀研究组用洛伦兹透射电子显微镜(LTEM)在Fe0.5Co0.5Si薄层中确切地在实空间看到了磁斯格明子的磁结构[18].在此以后将近十年的时间里,磁斯格明子领域经历了长足的发展,不仅实现了斯格明子的材料层出不穷,体系各有千秋,而且对斯格明子,尤其是单个斯格明子的操作有了更系统的方法.由于斯格明子的拓扑稳定性和在低电流下的易操作性,磁斯格明子很有希望成为下一代非易失性存储器件的磁性单元,关于其在具体内存和逻辑器件中的设计已有不少有意义的尝试[9,19−25].

图1 布洛赫型(a)和奈尔型(b)斯格明子的自旋构型Fig.1.Spin texture of Bloch type(a)and Néel type(b)skyrmion.

本文我们系统地解释了磁斯格明子的成因及其特殊的拓扑性质;总结了实现磁斯格明子的各种体系和材料,并对操控单个斯格明子的方法进行了梳理;最后对斯格明子未来的一些研究方向进行了展望.

2 斯格明子的拓扑性

在经典磁性体系中,可以简单地把每一个自旋看成是一个长度固定的向量,根据其各向异性能的不同,向量指向的态空间T也会有相应的变化.在单轴(easy axis)各向异性材料中,自旋只能与轴平行或是反平行两种状态,即呈现出伊辛态,T=Z2.在易面(easy-plane)各向异性中,自旋可以取向平面内的任意角度,这时T=S1,其中S1等同为二维中单位半径的圆环.值得指出的是,这里不同的磁各向异性既可以来源于材料中本身的晶格对称性,也可以来源于纳米尺寸中的形状各向异性[26].在长条状磁体中,沿着轴向的单轴各向异性起主导作用,而在亚微米级的纳米盘或是相当数量的磁性薄膜中,自旋更倾向于躺向面内呈平面态.而在多数的磁性体材料中,由于较弱的自旋轨道耦合作用,磁各向异性作用不大,自旋可以指向三维的各个方向,这时的自旋态空间T就为S2,即三维空间中的单位半径圆球面.

不同维度下的磁结构拓扑性就由同伦群Π:B→来描述,其中B是底空间的流形.一般地我们都把d维空间紧致化为Sd,那么同伦群Πd(T):Sd→就精确地描述了d维空间上的拓扑自旋构型(texture).在一维的情况下,特征的拓扑构型由图2表示.运用周期性边界条件,把一维的自旋链头尾相连,形成圆环,这时候B=S1.而自旋采用易面自旋态,T=S1,因此这个构型由Π1((S1):S1→S1所刻画,而这个同伦群又同构于整数集Z.也就是说圆环上的面内自旋态有无数多个各自拓扑不等价的非平庸构型,这些构型的拓扑性都可以用整数Q来标记,这个整数就是这个构型的拓扑数.在这里Q=ϕ/2π,其中ϕ是绕转圆环一周后自旋的转动角度.举例而言,图2(a)中Q=1,这是因为沿着圆环顺时针转动一圈,自旋转动了2π,而图2(b)和图2(c)中的Q分别为0和−1.这三种构型由于拓扑数的不同而拓扑不等价.特别地,如果把图2(a)的态转化为Q=0的铁磁态图2(c),自北极点顺时针绕转,自旋转动的角度不断加大,如图2(d)所示,最后导致北极点右侧自旋转动0◦,而其左侧自旋转动2π,因此这个变形不是连续的,两个构型拓扑不等价.

图2 一维下自旋的不同拓扑构型 (a)Q=1;(b)Q=0;(c)Q=−1;(d)从Q=1向Q=0拓扑态转变的示意图Fig.2.Spin textures with different topologies in 1D:(a)Q=1;(b)Q=0;(c)Q=−1;(d)schematic of the transformation from Q=1 to Q=0.

图2 (a)中径向张开的自旋构型可以推广到三维中二维球面的情况,如图3(a)所示,其中S(r)=.这时自旋为海森伯自旋,构型的拓扑性由Π2(S2):S2→S2所刻画,它对应的拓扑数Q描述了构型中所有自旋对二维球面的覆盖数.对于图3(a),Q=1,基于同样原因,它和图3(b)中的球面铁磁态拓扑不等价.通过球极映射的办法,我们可以把一个单位球面一一映射到二维平面上,从而把图3(a)中球面上的拓扑构型移植到二维平面中.具体做法如图3(c)所示,把单位球面放置于平面原点之上,连接球面北极点和平面内任意一点r的线段和球面相交于r0点,令r点的自旋为,最后在平面内形成了斯格明子的拓扑构型.令球面半径为R,由此构造的斯格明子的表达式即为

在原点处r=0,S=;而在无穷远处,S=.其中S的下标Néel表示这个斯格明子是奈尔构型的,即沿着任意一个经过原点的直线,自旋构型呈现出两重的奈尔磁畴构型.如果我们把这个斯格明子态绕着z轴转动90◦,即得到布洛赫态的斯格明子:

由于两种斯格明子态可以通过连续的转动互相转化,它们是拓扑等价的.根据拓扑数(也常称作拓扑荷(topological charge))的定义,可以由下式计算[27]:

图3 (a)Q=1的二维球面自旋;(b)Q=0的二维球面自旋;(c)球极映射示意图Fig.3.(a)Q=1 spin texture on 2D sphere;(b)Q=0 spin texture on 2D sphere;(c)schematic of the stereographic projection method.

可以得到对于上述两种斯格明子态,Q=1.事实上,对于任意一个自旋构型,拓扑荷可以表达为

值得指出的是,对于d维磁性系统,Sd−1,即d维空间的d−1维边界也有着重要的意义,同伦群描述了d维空间上的拓扑缺陷(defect)态.在三维中,同伦群Z则描述了磁单极子 (monopole)态,而在二维的情况下,同伦群描述了XY模型中的涡旋态(vortex).一维的情况比较特殊,它的边界只有独立的两个点,因此当自旋是伊辛态时,两端点的自旋是否相同就对应着一维自旋链中孤子(soliton)数目的奇偶性.与这些缺陷态不同的是,自旋构型是没有奇点的,自旋、能量的分布处处连续.所有这些丰富的拓扑构型和拓扑缺陷的形成和动力学构成了新兴的拓扑磁性物理的重要组成部分.

3 磁斯格明子与DM相互作用

(1)式和(2)式中讨论的斯格明子尺寸是无限大的,而我们关心的是有限大小的磁斯格明子,即使在三维的情况下,二维的斯格明子层层堆叠,形成一个斯格明子管道(tube),它的尺寸在横向上也是有限的.三维材料中一个稳定的有限磁构型的存在条件由Derrick的标度判据给出[28,29].假设有一个有限尺寸的稳定自旋构型S(r),它在通常的海森伯即各类磁性各向异性相互作用下的能量为

要实现有限尺寸的磁斯格明子,就需要在自旋之间引入新的相互作用.仔细考察可以发现,Derrick判据所没有包括的最简单的相互作用就是自旋的一阶空间导数项,如等,它们和海森伯相互作用一起,就会引入新的长度尺度,从而实现有限大小的磁斯格明子.由于这种新的相互作用只含一个空间导数,因此它们只存在于空间反演对称性破缺的磁性材料中,而这种相互作用就是DM相互作用,这种磁性材料就称为手性磁体[8].

DM相互作用是Dzyaloshinskii和Moriya分别由唯像模型和微观模型得到[15,16],如果两个磁性原子A和B连线的中点C不是反演中心,如图4所示,那么就存在如下的DM相互作用:

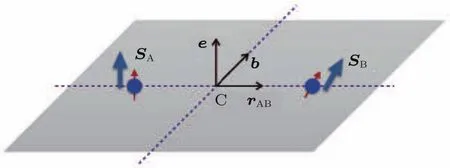
图4 Moriya定则示意图,其中r AB为从A指向B的单位向量,根据AB之间对称性的不同,D AB的方向也会相应地变化Fig.4.Schematic of the Moriya rules,r AB is the unit vector points from A to B.Direction of D AB will depend on the symmetry between A and B.

关于C做反演,两个自旋交换位置,能量因为自旋间的叉乘而反号,从而与反演对称破缺相一致.这里DAB是一个实空间中的向量,它的方向则由材料的空间对称性所决定,即Moriya定则[16]:

1)如果C是反演中心,D=0;

2)如果有一个镜面垂直AB且包含C点,则D平行此镜面;

3)如果有一个对称镜面包括两个自旋,则D垂直镜面;

4)如果有一个二度轴经过C点且垂直于AB,则D垂直于二度轴;

5)如果AB连线是一个n度轴,则D平行AB.

这些规则都可以通过对称性推演得到,比如说对于规则2,在镜面操作下,AB两自旋对调位置,A自旋垂直于镜面分量在此操作下不变,因而此分量必然和B自旋中镜面下变号的分量相耦合来保证能量不变,这个分量只能是平行于镜面,从而DAB在镜面内.别的规则也以此类推.

DM相互作用的微观机制是材料中的自旋轨道耦合,在很多情况下我们可以直接从自旋轨道耦合来直接理解DM.仍然考虑两个自旋AB,它们的自旋相互作用由从A到B的电子跳跃来完成,这个图像既直接适用于Ruderman-Kittel-Kasuya-Yosida(RKKY)相互作用中[30−32],也定性地成立于别的交换作用情况下[33].为了使交换能量最低,初态电子自旋和A自旋SA平行,在跳跃过程中,由于空间反演的破缺,晶体内存在原子电场e作用在电子上.于是在电子的随动坐标中,电场e从B向A运动,产生一个方向上的磁场b,电子自旋在b下做进动,从而在到达B时得到了一个b×SA方向上的分量.B上的自旋SB于是有了额外的交换作用:这正是DM相互作用,有了这个简单的物理图像,就不难理解为什么磁性薄膜之中也有DM相互作用,这种情况下,内建电场e垂直于薄膜,所以D向量躺在面内并且与自旋连线垂直.从这个分析中也可以看到,DM是自旋轨道耦合的一阶微扰,因此其相互作用能量较低,通常比相应的海森伯相互作用低了1—2个数量级,但是在很多情况下它并不可忽略,Moriya就用这个新的自旋作用成功地解释了铜基超导体中铜氧面的弱铁磁性,而手性磁体中的磁斯格明子就是由DM相互作用造成的.

仍然考虑两个自旋A和B,它们之间既有海森伯也有DM相互作用E=−JSA·SB+DAB·(SA×SB).其中铁磁海森伯相互作用希望两自旋平行,而DM相互作用希望两个自旋互相垂直.两者竞争的妥协结果就是两自旋互成一个大小约为D/J的小角度.在一列自旋的情况下,自旋转角不断累积,最终形成了图5(a)和图5(b)所示的自旋螺旋态(spin helix).在DM相互作用D比较小的情况下,螺旋的周期近似为λ=2Ja/D,其中a是晶格常数.注意到螺旋态的总自旋为零,所以在一定的磁场下它不再是体系的基态.在三维块材的情况下,有限磁场下体系的基态为锥形态(conical),如图5(c)所示.有趣的是,在有限的温度和磁场下,在居里温度附近就出现了一个之前被称为A相的斯格明子晶体相,它的存在是由Mühlbauer等[17]由小角度中子散射在MnSi单晶中确定的.在这个相区中,磁斯格明子在垂直于磁场的平面内形成三角密堆积,并沿着磁场做三维堆叠.这个磁斯格明子晶体可以理解为三个互成120◦的螺旋态和铁磁背景的线性叠加:

其中M为方向的磁矩,q为动量空间中的向量.正是由于铁磁背景的存在,斯格明子晶体能够从外磁场的塞曼(Zeeman)能中降低能量,相比之下,螺旋态没有静磁矩,它的塞曼能比斯格明子要来得高.而另一方面,斯格明子的能量虽然比锥形态能量较高,但两者实际上非常相近.在有限温度下,由于热力学涨落,在高斯修正下得到斯格明子晶体的自由能比锥形态来得更低,这也是磁斯格明子在一系列手性磁体中的成因[34,35].同样因为强热力学涨落的存在,斯格明子晶体到顺磁态的相变从二阶变成了一阶[36].

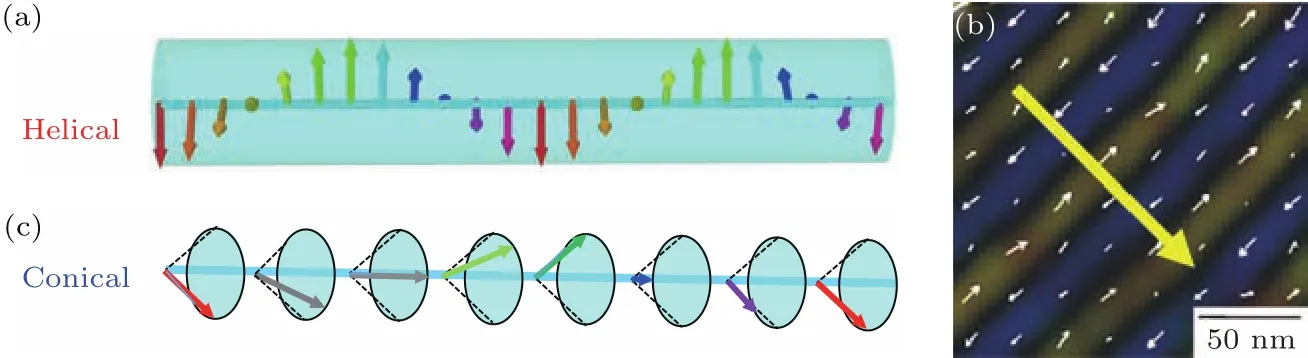
图5 (a)螺旋态自旋排列;(b)螺旋态的实空间成像图[18];(c)锥形态自旋排列Fig.5.(a)Helical state;(b)real space image of the helical state[18];(c)conical state.

在很多情况下,特别是将来可能的应用中,我们更关心磁斯格明子在二维薄膜中的形成情况.特别地,当薄膜厚度小于锥形态周期时,锥形态被完全抑制,斯格明子态向低温区扩大,最终能够实现零温的斯格明子基态,斯格明子／螺旋态和斯格明子／铁磁态之间的转变磁场Bc都在µBBc∼D2/J的数量级上,其中µB是玻尔磁子[37].

4 新兴电动力学

考虑到多数斯格明子材料都有一定的导电性,其中的电子输运以及电子和磁构型的相互作用一直是这个领域的研究热点之一.磁斯格明子的非平庸拓扑性也同时诱导了这类材料电子输运中的丰富物理,其中最突出的就是新兴(emergent)电动力学[38−42].由于电子自旋和局域磁矩之间较强的洪特耦合(Hund’s rule coupling),电子的自旋总是与局域磁矩相平行,也就是说电子自旋的空间从原本的二维希尔伯特空间(Hilbert space)约束到了一个局域的一维自空间.和绝热近似下贝里相位(Berry phase)的物理一致,这种对希尔伯特空间的约束就会诱导出一个等效的新兴规范场及其对应的新兴电磁场[43].具体而言,导电电子的哈密顿量可以写为其中m是电子的有效质量;而JH是洪特耦合的强度.在大JH的极限下,电子自旋严格平行于于S,其自旋态满足将哈密顿量通过投影算符投影到这个空间中,就可以得到描述导电电子的有效哈密顿量,这里的a就是新兴U(1)规范场,,它对应的新兴磁场则为

其中c为光速.可以看到,这个表达式的主要部分S·(∂xS×∂yS)也出现在了拓扑荷的表达式中,因此,拓扑荷的整数性就对应着新兴磁场的磁通量子化,

这个新兴磁场作用在导电电子上,就形成了对应的霍尔效应,由于这个霍尔效应是由磁斯格明子的拓扑造成的,我们把它称为拓扑霍尔效应(topological Hall effect),它在各类手性磁体中都有报道[38,42,44−51],拓扑霍尔效应的测量已经成为了表征斯格明子的重要电学手段.在这里,横向电阻ρxy有三方面的贡献:其中右边的三项分别为为普通霍尔效应[52]、反常霍尔效应[5]和拓扑霍尔效应.R0和RS分别是普通霍尔系数和反常霍尔系数.反常霍尔效应有多种来源,其中的偏散射(skew scattering)使RS正比于纵向电导ρ:RS=cρxx,而side jump和本征(intrinsic)位效应则有在手性磁体中,项起主导作用,所以可以通过同时测量霍尔电阻、磁矩和纵向电导就能够拟合出R0和b,从而得到拓扑霍尔电阻.值得注意的是,这里的一个重要假设是系数b为常数,在手性磁体中b基本与外磁场无关[47,48,56],但是在别的斯格明子体系中是否成立还有待商榷,而b和温度的关系也不明确.另外,反常霍尔效应中的本征部分由动量空间中的贝里相位所提供,而拓扑霍尔效应来源于磁构型的实空间拓扑性,两个空间中的拓扑同时构成了这类体系中丰富的输运现象[57,58].但是值得注意的是,拓扑霍尔效应虽然来源于构型的整体拓扑,但是对于一个有局域自旋倾斜(canting)而整体拓扑荷为零的磁构型,横向电子输运也会存在[59,60].

5 磁斯格明子材料体系

自2009年磁斯格明子首次发现至今,实验上已经确认了多种磁斯格明子材料体系,比如手性磁体、磁性薄膜、Heusler化合物、阻挫磁体等.由于这些材料体系具有不同的物理特性,因此其中斯格明子的尺寸、稳定性及动力学性质也不尽相同,这极大地丰富了磁斯格明子研究及应用材料的选择范围.下面我们对现有的磁斯格明子材料体系进行讨论,并在表2中总结了一些常见的斯格明子材料.

5.1 手性磁体

磁斯格明子最早发现于手性磁体B20类型化合物MnSi中[17].由于晶胞内缺乏中心对称性,手性磁体具有自发的体类型DM相互作用.在B20化合物中体类型DM相互作用下,斯格明子的构磁型一般表现为布洛赫型(Bloch-type).手性磁体中,根据材料的不同,磁斯格明子的尺寸一般在10—100 nm之间.斯格明子的尺寸与手性磁体的螺旋周期有关.上文已经提到,螺旋周期(L)一般取决于海森伯近邻相互作用和DM相互作用的比值.目前手性磁体中观测到的最小螺旋周期存在于MnGe中,约为3 nm,这是由于MnGe中具有很强的DM相互作用[61].研究表明,除斯格明子外,MnGe还蕴含着丰富的拓扑磁性结构[62,63],因此其具有潜在的研究价值.手性磁体中的DM相互作用完全取决于材料本身的性质,因此对单一手性磁体材料中DM相互作用的调制较为困难.但是,最近有研究表明,利用外延生长可以得到高质量的B20类型手性磁体超晶体,该研究还预言了通过该类超晶体调控DM相互作用的可能性,为手性磁体材料的优化提供了一种新的思路[64].

手性磁体在零磁场下的基态通常为螺旋态,稳定的斯格明子相通常需要通过施加外部磁场来得到,这极大地限制了手性磁体在实际应用中的价值.因此,实现手性磁体中零场下稳定的斯格明子尤为重要.针对如何实现手性磁体中具有零场稳定性的斯格明子,目前主要有两种思路:一种是利用受限体系来实现磁斯格明子的零场稳定性,这种思路利用了受限体系中磁偶极相互作用引发的形状各向异性及特定的边界条件来提升磁斯格明子的稳定性[65,66];另外一种思路是利用外延生长手性磁体薄膜,来实现磁斯格明子的零场稳定性[67].这两种思路目前都已经通过实验证明了其可行性,为将来手性磁体材料的优化提供了重要依据.

另一方面,手性磁体的居里温度通常低于室温,这也为手性磁体的实际应用带来了挑战.大部分B20化合物的居里温度远低于室温,其中FeGe是已发现的具有最高斯格明子相温度的B20材料,其斯格明子相可稳定存在于280 K,然而该温度仍然略低于室温[47,68].在一类非B20类型的手性磁体β-Mn型Co-Zn-Mn合金中,斯格明子相可稳定存在的最高温度为400 K,并且具有零场稳定性,这种合金的发现极大地拓展了手性磁体材料在斯格明子实际应用中的潜力[69,70].

拥有斯格明子相的手性磁体材料中,绝大部分为金属材料.Cu2OSeO3是目前手性磁体中罕见的绝缘体材料,并且具有多铁性[71].虽然同属于B20结构类型,但和一般B20类型化合物相比,Cu2OSeO3中铜原子的出现使其晶格结构更为复杂[72].Cu2OSeO3中斯格明子相的出现通常伴随着宏观电极化的变化,并且由于其本身的电绝缘性和多铁性,这种材料中有可能实现通过纯电场操控斯格明子,从而避免产生额外的焦耳热[73].但Cu2OSeO3的居里温度很低(约为58 K),因此若要向实际应用靠拢,实验上应寻找更多具有更高居里温度的多铁绝缘手性磁体.除金属和绝缘手性磁体材料外,磁性半导体材料GaV4S8中也具有斯格明子相,并且其中的斯格明子磁构型为奈尔型,这是因为GaV4S8的对称性与B20化合物不同,提供了对称性不同的DM相互作用[74].

表1 可能存在斯格明子相的材料点群Table 1.Possible material point groups that could host skyrmion phase.

目前已有理论研究通过对称性及群论分析建立了一套系统寻找可能具有各类斯格明子相手性磁体的方法[75].表1中总结了利用该方法得到的可能具有斯格明子相的点群,传统的B20化合物属于其中的T群.利用这套理论方法,人们预言了O群材料中存在磁斯格明子相的可能性,并在实验观上测到了O群材料FexCo1−xRh0.5M o3N中存在的斯格明子相,验证了该方法的可靠性.除FexCo1−xRh0.5Mo3N外,该对称性理论框架中还包含了上文提到的β-Mn型Co-Zn-Mn合金(O群)和磁性半导体GaV4S8(C3v群),并可以很好地解释这些材料中的DM相互作用对称性及斯格明子磁构型.这套理论方法为系统搜寻斯格明子手性磁体材料提供了可靠的理论依据,可以有效地应用于未来斯格明子新材料的开发及优化.

5.2 磁性薄膜及多层膜

除晶胞内中心对称性破缺产生的自发体类型DM相互作用外,DM相互作用还可以在磁性薄膜/重金属界面上产生.早在1990年,理论研究便预测了这类磁性薄膜结构中存在DM相互作用的可能性[76].在磁性薄膜/重金属界面上,由于磁性薄膜界面镜面对称性的缺失及重金属中的强自旋-轨道耦合,两个近邻磁性原子之间会产生一种由重金属原子传导的非直接交换相互作用,即界面DM相互作用,如图6(a)所示.因为材料对称性的不同,界面DM相互作用的对称性也与B20化合物中体类型DM相互作用的对称性不同,在界面DM相互作用下的斯格明子磁构型一般表现为奈尔型.

图6 (a)磁性薄膜体系中DM相互作用示意图,其中d为DM相互作用向量[83];(b)利用自旋极化扫描隧道显微镜得到的单层Fe/Ir(111)中斯格明子的磁构型,插图为实空间磁够型的傅里叶变换[77];(c)铁磁薄膜/反铁磁体异质中的斯格明子[85];(d)利用调控层间相互作用得到的室温下稳定的斯格明子[78];(e)室温下纳米条带和纳米盘中稳定的单个斯格明子[83];(f)通过第一性原理计算得到的Co薄膜中DM相互作用的强度[79]Fig.6.(a)Schematic of interfacial DMI in magnetic thin films,d rep resents the DM vector[83];(b)SP-STM image of skyrmion magnetization in monolayer Fe/Ir(111),inset shows the Fourier transformation of magnetization in real space[77];(c)skyrmion in FM/AFM heterostructure[85];(d)skyrmions at room temperature stabilized through interlayer exchange coup ling in ultra-thin films[78];(e)room temperature isolated skyrmion in magnetic nano-tracks and nanodisks[83];(f)calculated amplitude of DMI in Co thin films[79].

奈尔型斯格明子最早发现于单层Fe/Ir(111)中,在这种材料体系中,界面DM相互作用非常强,因此斯格明子的大小仅为1 nm(图6(b)),是目前为止实验上观测到的尺寸最小的斯格明子[77].虽然这类材料中斯格明子尺寸小并具有零场稳定性,但是在这类单层膜或超薄磁性膜中,斯格明子的稳定温度通常小于10 K.为了提高斯格明子相的温度,有研究利用铁磁层间相互作用大幅提升了斯格明子相的温度.通过细致调节层间相互作用,实验发现斯格明子可在室温零场下稳定(图6(d)),证明了超薄铁磁膜中磁斯格明子的应用潜力[78].

除单层膜及超薄铁磁膜外,近年来斯格明子材料体系的另一个研究热点是通过磁控溅射生长的磁性薄膜/重金属异质结构及其多层膜结构.磁控溅射是工业界中广泛应用的材料生长技术,其在磁存储领域具有重要的应用,是当前磁存储媒介生长的主要工具.磁斯格明子在该类材料中的研究与其实际应用紧密相连,可以促进斯格明子的应用转化,因此引起了人们的广泛研究兴趣.除此之外,这类材料中的界面DM相互作用及垂直磁各向异性可以通过调控薄膜厚度、材料组合等参数进行人工调制,赋予了该材料体系极大的自由度,从而能够更好地优化斯格明子的尺寸、稳定性和动力学性质.

磁性薄膜/重金属异质结构及其多层膜结构目前有两种主要的材料结构.一种是重金属/磁性薄膜/金属氧化物材料结构,如Pt/Co/MgO纳米结构、Pt/CoFeB/M gO纳米结构和Ta/CoFeB/TaOx纳米结构[79−81].如图6(f)所示,通过第一性原理计算,人们发现在这类结构中,界面DM相互作用不仅来源于重金属(如Pt,Ta)与铁磁层的界面,还来源于金属氧化物与铁磁层的界面.第一性原理计算还表明,铁磁层与金属氧化物界面的界面DM相互作用与该界面上的电荷转移和电极化有关,并预言除了金属氧化物外,表面氧化也可以提升这类结构中DM相互作用的强度,从而缩小斯格明子的尺寸并提升其稳定性[82].而另外一种材料结构是重金属/磁性薄膜/重金属结构,如[Ir/Co/Pt]10多层膜结构和[Pt/Co/Ta]15多层膜结构[80,83],图6(e)展示了这类多层膜结构中的单个斯格明子.在这类结构中的第一性原理计算表明,在单独的Ir/Co和Pt/Co结构中,两种重金属所提供的DM相互作用手性方向是相反的,但是由于在这类三明治结构中,两种重金属分别位于上下表面(即Ir/Co/Pt),因此它们最终提供的DM相互作用手性一致(如图6(a)所示),并能通过共同作用来提升DM相互作用的强度[84].

另外,除了上面提到的两种结构,最近实验上还发现了一些新奇的磁性薄膜材料体系,这些材料体系也许能为薄膜体系的优化提供一些新颖的思路.第一种材料体系是反铁磁金属薄膜与铁磁薄膜的异质结构IrMn/CoFeB/MgO/.实验上已经发现IrMn/CoFeB/MgO结构中具有斯格明子相[85],如图6(c)所示.同时,人们还发现其中的DM相互作用强度对反铁磁层的厚度依赖关系不同于重金属/铁磁薄膜体系,理论上对此现象尚无明确的解释[86].除此之外,该结构还可以通过铁磁-反铁磁体之间的交换偏置来为斯格明子提供额外的零场稳定性.另一种新奇的材料体系是稀土亚铁磁多层膜结构[Pt/Gd25Fe65.6Co9.4/MgO]20[87].该材料的亮点是其中使用了亚铁磁材料,可以抑制斯格明子的霍尔角.斯格明子在运动过程中存在斯格明子霍尔效应,通常会产生一垂直于其运动方向的速度,使斯格明子的前进方向发生偏移,进而影响其在实际应用中的可操控性.理论预测在合成反铁磁薄膜或反铁磁材料中,由于两种磁性子晶格中的磁矩方向相反,斯格明子霍尔效应可以被抵消,从而提升斯格明子的运动速度[88−90].亚铁磁材料中,虽然两种磁性子晶格的磁矩无法完全抵消,但是实验上发现其已经显现出对斯格明子霍尔角的抑制和对斯格明子运动速度的提升,初步验证了理论的预测.

磁性薄膜结构中,斯格明子均可在室温下稳定存在,并且由于这类磁性薄膜具有良好的垂直磁各向异性,斯格明子的零场稳定性也有所保证.根据材料的不同,磁斯格明子在薄膜体系中的尺寸通常为100—1000 nm,在一些实验中斯格明子的尺寸可以达到40 nm.从斯格明子的实际应用角度出发,该类材料已经具备一些良好的物理性质,但是仍有一些问题亟待解决.首先,磁斯格明子的尺寸尚未达到应用的需求(小于10 nm),目前仅有少数实验可以实现尺寸在100 nm以下的斯格明子,因此,如何继续降低斯格明子的尺寸仍是薄膜材料优化的重要方向.其次,由于使用磁控溅射的生长方法,磁性薄膜的不均匀度和粗糙表面是无法避免的,这些因素会带来不均匀的DM相互作用、磁各向异性及不同程度的钉扎效应,从而影响斯格明子传输的效率[91,92].因此,在实验上也应考虑如何进一步提高薄膜的质量,或通过其他方式来优化材料,从而最大程度地提高斯格明子的传输效率.

5.3 其他材料体系

斯格明子不仅可以在手性磁体和磁性薄膜中依靠DM相互作用稳定存在,还可以在缺少DM相互作用的人工结构中稳定存在[93−96].这类人工结构主要由具有垂直各向异性的铁磁薄膜和具有磁涡旋态的纳米盘组成.经过特殊设计的纳米盘阵列被放置于具有垂直各向异性的铁磁薄膜之上,经过一系列施加外磁场的初始化过程,纳米盘中的磁构型由铁磁态转变为磁涡旋态,此时,由于铁磁薄膜和纳米盘间的交换相互作用,该磁涡旋结构会刻印到铁磁薄膜中,从而在铁磁薄膜中形成磁斯格明子晶体态,如图7(a)和图7(b)所示.在这类人工结构中,由于斯格明子来源于纳米盘中磁涡旋构型的刻印,因此其磁构型表现为布洛赫型.另外,由于磁涡旋核心本身也具有不同的极化方向,因此通过改变外磁场的初始化过程,当磁涡旋核心极化方向平行于铁磁薄膜中自旋极化方向时,该类结构中还可以产生拓扑数为0的平庸磁结构.在这类磁结构中,斯格明子可在室温下具有零场稳定性,其尺寸通常为数百纳米到2µm.在人造结构的基础上,还有理论研究提出可利用手性磁体来代替下层的垂直磁各向异性薄膜,形成混合斯格明子态[97].该类异质结构能够提升斯格明子的稳定性和流动性,这种不同材料体系的混搭也有可能开辟斯格明子应用的新方向.

常见的斯格明子磁构型为布洛赫型、奈尔型或两者的混合态.然而在一类具有中心对称性的磁体,如La2−2xSr1+2xMn2O7和MnNiGa中,斯格明子会2个一对形成被称为双斯格明子的束缚态,如图7(b)所示,双斯格明子在一定温度磁场区间内,也会形成类似斯格明子的三角晶体[98,99].双斯格明子的尺寸一般在90—200 nm之间,在MnNiGa中,双斯格明子还具有超宽的温度稳定区间并有丰富的电学性质.这类中心对称材料中双斯格明子的发现为探索斯格明子新材料提供了新的思路.另外由于具有中心对称性,这类材料中并不具备DM相互作用,因此双斯格明子的产生应该是由一些其他相互作用的竞争导致的,但目前其具体产生机制仍然缺乏一个理论上完备的解释.

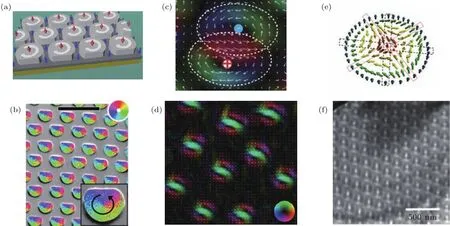
图7 (a)人造斯格明子晶体的理论示意图[93];(b)通过极化分析扫描电镜得到的磁性薄膜中人造斯格明子晶体的磁构型[94];(c)双斯格明子的磁构型[98];(d)双斯格明子晶体;(e)反斯格明子磁构型[100];(f)反斯格明子晶体[100]Fig.7.(a)Magnetization arrangements of artificial skyrmion lattice[93];(b)scanning electron microscopy with polarization analysis image of artificial skyrmion lattice in magnetic thin films[94];(c)spin texture of biskyrmion[98];(d)biskyrmion lattice[98];(e)spin texture of antiskyrmion[100];(f)antiskyrmion lattice[100].

表2 不同材料体系中斯格明子的尺寸稳定磁场及温度区间总结,其中M L代表单层(monolayer)Table 2.Size,magnetic field and temperature window of stabilized skyrmion in different materials,M L rep resents monolayer.

类似图2(a)和图2(c)中的磁涡旋和反磁涡旋,斯格明子也具有其相反的准粒子磁构型,即反斯格明子.反斯格明子的涡度为负整数,与普通斯格明子相反,因此其拓扑数的符号也与斯格明子相反.在Heusler化合物Mn1.4PtSn和Mn1.4Pt0.9Pd0.1Sn中,这些材料的D2d对称性改变了DM相互作用的对称性,进而形成了稳定的反斯格明子态[100],如图7(e)和图7(f)所示.这些反斯格明子的尺寸约为150 nm,并具有很宽的温度稳定区间.由于Heusler化合物本身具有极大的物理性质调控自由度,其晶体结构及对称性、磁各向异性和磁矩等均可以调节,这类材料还有可能具有反铁磁性,从而具有可以形成反铁磁反斯格明子的可能性.因此Heusler化合物中的反斯格明子也可能具有广阔的应用前景.除Heulser化合物外,理论还预测在超薄磁性膜(2 ML Fe/W[110])中反斯格明子也有可能稳定存在,但是该理论尚未得到实验验证[101].

除普通铁磁和亚铁磁材料外,阻挫磁体中也有稳定的斯格明子态存在,但是其产生机制不依赖于常见的DM相互作用.在阻挫磁体中通常存在多种不同的近邻相互作用,理论推测阻挫磁体中的斯格明子是由于这些近邻相互作用之间的竞争而产生的[102,103].阻挫磁体本身便与拓扑性紧密相连,其中包含了许多奇异的量子态,如Kitaev量子自旋液态,是拓扑量子计算的备选材料[104,105].而从斯格明子研究的角度出发,阻挫磁体也具有独特的物理特性.具有DM相互作用的体系中,其手性由DM相互作用矢量决定,因此这些体系中的斯格明子的手性是独一无二的.但在阻挫磁体中斯格明子的存在并不依赖于DM相互作用,其手性并没有特别的取向,因此阻挫磁体中的斯格明子可以展现出多种能量简并的不同手性磁构型.对于阻挫磁体中的斯格明子,理论早已预言了其稳定存在的可能性,并指出了它们具有能量简并态[102,103,106].而实验上也已经在阻挫磁体Fe3Sn2中观测到了磁斯格明子的存在,并且发现其具有多种不同的磁构型,如图8所示[107].但在该体系中,理论和实验尚不能很好地相互印证.比如Fe3Sn2中发现的一些具有多同心圆环的斯格明子磁结构,其理论解释还有待研究.另外,如何寻找更多具有斯格明子相的阻挫材料也是实验和理论研究的重点.除此之外,研究阻挫磁体中磁斯格明子和其他奇异量子态的关联性,如Fe3Sn2中的狄拉克费米子和斯格明子磁序的关联性,也对探索潜在的拓扑量子材料有着重要意义[108].

图8 通过洛伦兹透射电镜得到的(a)300 K和(b)250 K下斯格明子和周围条带畴的图像;(c)300 K和(d)250 K下通过分析得到的(a),(b)中方块内斯格明子的具体磁构型[107]Fig.8.LTEM images of skyrmions and strip domains at(a)300 K and(b)250 K;(c)and(d)are the detailed skyrmion spin texture within the box in(a)and(b),respectively[107].

6 磁斯格明子的产生和湮灭

在通往磁斯格明子实际应用的道路上,需要解决的一大难题是如何利用高效、快速、低能耗的手段产生和湮灭单个斯格明子.在实际应用中,人们将斯格明子的存在与不存在两种状态(一般对应斯格明子态和铁磁态)定义为信息比特中的“1”和“0”.因此,斯格明子的产生和湮灭即相当于传统信息存储中的写入信息“1”和“0”的操作.

自斯格明子存储应用的概念提出以来,理论研究已经提出了多种可行的斯格明子产生湮灭方法,而其中部分已经得到了实验的验证.在自旋电子学的大背景下,一种最直接的方法便是利用自旋转移力矩(spin transfer torque,STT)来产生和湮灭斯格明子[115−117].STT本身具有两种不同的作用方式,一种由面内电流主导(current-inplane,CIP)[117],一种由垂直面电流主导(current perpendicular-to-plane,CPP)[115].

对于CIP结构,理论提出可以利用特殊设计的边界条件来产生斯格明子,如人工制造一个缺口[118].由于DM相互作用和磁偶极相互作用,在铁磁态下,样品边界的自旋会具有一个不可忽视的面内分量,并且该分量的方向取决于样品边界的形状.利用人工缺口边界自旋的面内分量,在施加面内电流的情况下,便可以在边界附近产生斯格明子,图9(a)—(c)展示了这类结构中斯格明子产生的过程.最近已经有实验在磁性薄膜中证明了该理论预测[119].除了利用特殊设计的边界条件外,还可以利用纳米条带中的宽窄变化来实现斯格明子的产生.其中一种方法是利用磁畴壁与斯格明子的相互转化,通过磁畴壁从窄区域到宽区域的运动,来实现磁斯格明子的产生[120],如图10(d)所示.这种方法不仅可以有效地产生斯格明子,还将斯格明子与传统磁畴壁联系到了一起,对斯格明子和磁畴壁的混合应用具有重要指导意义.另外一种方法则是利用了宽窄条带中非均匀纳米结构导致的非均匀电流,如图10(b)所示,该非均匀电流会对结构中产生的磁畴条带施加一个扩张力,使磁畴条带断裂并形成斯格明子[81].实验上已经证明通过精细的调控电流脉冲的大小和持续时间,可以精确控制斯格明子产生的数量,图10(c)展示了该实验中单个斯格明子的产生和移动过程,进一步在实验上证明了斯格明子赛道存储的可行性[121].

对于CPP结构,一种方法是利用自旋阀或磁性隧道结结构,这类结构中有一层额外的铁磁薄膜作为自旋极化层,通过垂直施加电流最终在斯格明子材料薄膜中注入一个自旋极化电流,如图11(a)所示[122].目前这种斯格明子的产生方法是斯格明子赛道存储概念中广泛使用的理论方法.最近,已经有实验研究部分证明了自旋阀结构中产生斯格明子的可能性,但是单个斯格明子的产生和湮灭还没有实现[123].另外还有一种方法是利用自旋极化扫描隧道显微镜(spin-polarized scanning tunneling microscopy,SP-STM)向斯格明子材料薄膜中注入自旋极化电流,从而产生斯格明子[110].利用SP-STM,实验上还可以对斯格明子材料薄膜施加局域电场,如图11(b)所示,该局域电场也可以实现对单个斯格明子的产生和湮灭操作,并且其电场产生的方法具有低于电流产生方法的能耗[109].该类实验展示了进行精确的单个斯格明子产生和湮灭的可行性,但是因为依赖SP-STM,这类技术在实际应用中具有很大的局限性.

除电学方法外,还有一些其他具有应用潜力的斯格明子产生湮灭方法.激光是凝聚态物理中一种常用的实验手段,研究表明,对斯格明子磁性薄膜施加激光脉冲也可以实现斯格明子的产生和湮灭[124−126].这类方法的机制类似于目前磁存储技术中的热辅助磁存储技术(heat assisted magnetic recording),通过瞬间提升温度来改变磁体中的磁状态[127].但是这类方法目前仍局限于大规模产生斯格明子,尚无法实现单个斯格明子的操控.

图9 (a)—(c)通过人工缺口达成的斯格明子产生过程[118];(d)实验上通过人工缺口达成的斯格明子产生,蓝色虚线内为样品区域,施加一个电流脉冲后,在缺口附近产生了一个斯格明子[119]Fig.9.(a)–(c)The process of single skyrmion creation in a notch geometry[118];(d)experimental demonstration of skyrmion creation in a notch geometry.The area within the blue dash line is the sample area.After an applied current pulse,a skyrmion is created near the notch[119].

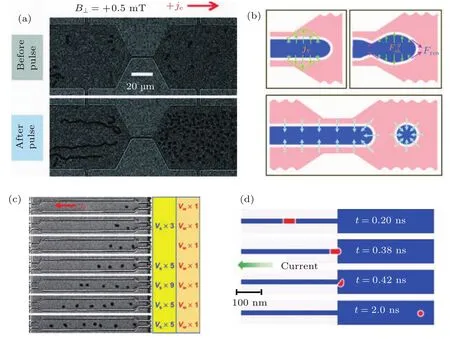
图10 (a)实验上通过纳米条带的宽窄收缩来产生斯格明子的过程[81];(b)纳米条带中不均匀电流对磁畴壁施加的不均匀力示意图[81];(c)纳米条带中单个斯格明子的产生[121];(d)斯格明子和磁畴壁的转化[120]Fig.10.(a)Creation of skyrmions through a nano-constriction[81];(b)schematic of the non-uniform current distribution and the corresponding non-uniform force distribution on the magnetic domain wall[81];(c)single skyrmion creation in a nanostripe[121];(d)conversion between skyrmion and magnetic domain wall[120].

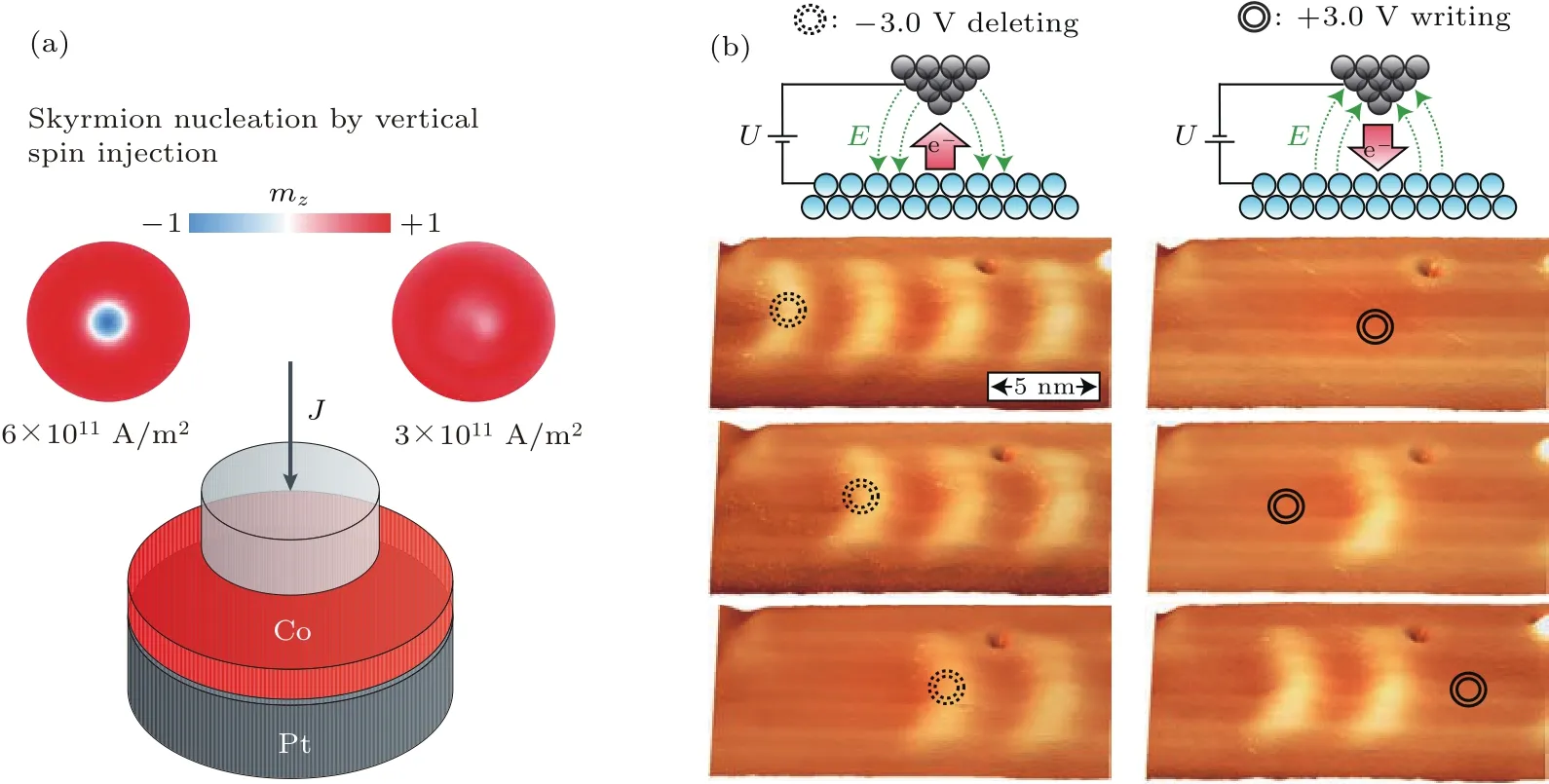
图11 (a)自旋阀或磁性隧道结产生斯格明子的示意图[122];(b)通过电场产生和湮灭单个斯格明子的过程[109]Fig.11.(a)Schematic of skyrmion creation in a spin valve or magnetict tunnel junction structure[122];(b)electric filed creation and annihilation of single skyrmion[109].

在特殊设计的十字结构中,斯格明子还可以通过自旋波来产生,这类方法利用了斯格明子/非斯格明子材料异质结构,通过自旋波的诱导,在斯格明子材料中(十字结构的交叉点)产生斯格明子,这种方法可以实现斯格明子的非局域产生和湮灭[128].另外在多铁斯格明子材料中,还可以通过施加局部电场利用其多铁的性质来产生和湮灭斯格明子[129].还有理论预测,利用压电材料和磁弹效应,也可以产生和湮灭斯格明子[130,131].以上这些理论提案均尚未得到实验验证,但为斯格明子的实验和实际应用提供了丰富的思路.

7 磁斯格明子探测

斯格明子发现的初期,人们只能利用小角度中子散射和洛伦兹透射电镜来对斯格明子进行探测,极大地限制了斯格明子的研究.随后,人们开发了多种斯格明子的探测方法,包括自旋极化扫描隧道显微镜、共振X射线散射、磁力显微镜、磁光克尔显微镜、自旋极化低能电子显微镜、氮空位色心磁力测定、X射线显微镜、电子全息显微镜等[66,77,78,80,81,87,132−138].这些实验探测手段各有所长,给斯格明子的研究带来了极大便利.

这些探测方法中,除中子散射外,其余方法均可对材料中斯格明子在实空间的磁构型进行一定程度的解析.在空间分辨率上,洛伦兹透射电镜、自旋极化扫描隧道显微镜、自旋极化低能电子显微镜、X射线手段和电子全息显微镜具有较大的优势,其空间分辨率可以达到10 nm甚至原子尺度(自旋极化扫描隧道显微镜)[139],可以对斯格明子的详细磁构型进行解析,但是这些手段在测量温度、测量磁场及对测量样品的尺寸要求上仍有限制,对一些宽温度磁场区间和特定尺寸的样品进行测量依然具有挑战.另一方面,一些具有较快时间分辨率的手段则在斯格明子动力学的探测中具有明显的优势,比如X射线显微镜和磁光克尔显微镜,这些手段在研究斯格明子的产生、湮灭及输运方面发挥了重要作用.中子散射也能在一定程度上捕捉到斯格明子晶体的动力学,但是其时间尺度远大于上面提到的单个斯格明子动力学过程,并且对样品的单晶性有很大的要求[42,73].最近还有研究报道了具有超快时间分辨率的LTEM,可以用来研究斯格明子的产生和湮灭,极大地扩展了LTEM在斯格明子研究中的应用范围[125].虽然上述手段都能够对斯格明子进行测量,是当前斯格明子研究的重要表征手段,但它们都需要大型设备的支持,其手段都较为复杂,难以在未来以斯格明子为基础的实际器件中应用.

在应用器件中,人们最感兴趣的仍然是利用电学手段对单个斯格明子进行探测,这类探测是实际应用中最为需要实现的技术.在斯格明子赛道存储概念中,人们提出利用自旋阀中的巨磁阻效应(giant magnetoresistance,GMR)和磁性隧道结中的隧道磁电阻(tunneling magnetoresistance,TMR)来进行斯格明子的电学测量,如图12(a)所示.因为斯格明子的磁构型具有与铁磁态极化方向相反的核心,因此当斯格明子通过自旋阀或磁性隧道结时,会产生与铁磁态不同的GMR或TMR.实验上对这种方法已经进行了初步的验证,但是对单个斯格明子的测量仍然有待验证.

电学探测中,还有一种被称为非共线磁阻(non-collinear magnetoresistance,NCMR)的手段[142,143].在尺寸较小的斯格明子中,相邻自旋的方向角度差异比较大,该角度差异会影响材料中电子的能带结构,从而影响材料的磁阻.而在铁磁态中,由于相邻自旋完全平行,因此并不会产生NCMR,从而将铁磁态与斯格明子态区分开来,如图12(c)所示.实验上发现,对于极小尺寸(1 nm左右)的斯格明子,NCMR在斯格明子形成区域附近的变化可以达到100%,但是其净变化与实际测量面积有关,因为铁磁态背景并不具备NCMR,会降低整体测量的净NCMR.除此之外,NCMR只依赖于相邻自旋间的角度差异,即其非线性自旋结构,假如材料中具有一些其他非斯格明子的非线性自旋结构,也可能导致NCMR的变化,从而错误地进行斯格明子的电学测量.

霍尔效应也可以被用来进行斯格明子的电学探测,其测量结构如图12(b)所示.首先磁体中会展现反常霍尔效应,由于斯格明子自身核心中携带的反向极化自旋,斯格明子的磁结构可以通过反常霍尔效应来探测.除反常霍尔效应外,磁斯格明子本身的拓扑性还会导致拓扑霍尔效应,该效应与斯格明子的拓扑非平庸性紧密相连,也可以用来进行斯格明子的探测[141,144].结合光学手段,实验上已经发现可以通过反常霍尔效应来对磁性薄膜体系中的单个斯格明子进行电学探测[135,145].图12(d)中显示了斯格明子通过霍尔条时系统霍尔信号的变化.研究人员提出,这类探测中发现的拓扑霍尔信号要比反常霍尔信号低三个数量级.这可能与材料体系本身的性质相关,薄膜体系中测得的拓扑霍尔信号一般远小于手性磁体中的拓扑霍尔信号,其原因还有待研究.而材料中电子的能带结构对拓扑霍尔效应的影响也尚不可知,理论研究曾预测通过控制材料中载流子的组成,可以调控拓扑霍尔效应,并能实现拓扑自旋霍尔效应,但是至今为止仍没有类似的实验研究[146].另一方面,现在该电学测量方法的电阻变化依然很小,进一步提升电阻的变化不仅需要材料方面的优化,也需要对器件的结构进行优化.

图12 (a)通过自旋阀或磁性隧道结测量斯格明子磁阻的示意图[140];(b)通过霍尔效应来测量斯格明子的示意图[141];(c)实验上测量的斯格明子非共线磁阻[142];(d)实验上通过霍尔条测量的斯格明子的霍尔信号[135]Fig.12.(a)Schematic structure of single skyrmion detection via a spin valve or magnetic tunnel junction[140];(b)schematic structure of single skyrmion detection via Hall effect[141];(c)experimental measured NCMR signal of a single skyrmion[142];(d)experimental measured Hall resistance of a single skyrmion[135].

8 结论与展望

自从实验上发现磁斯格明子的将近十年中,磁斯格明子的物理探索进入了一个高速发展时期,如上所述,各种实验材料层出不穷,而且对于斯格明子,特别是单个斯格明子的操作研究成果也不断涌现.这方面的研究成果也极大地促进了拓扑磁性和自旋电子学的发展,也为下一代自旋电子器件提供了新的可能性.但是,磁斯格明子还是有很多的问题亟待攻克,还有一些有意义的基础研究需要更多的探索.

在材料方面,室温小尺寸的斯格明子材料还在寻找中,特别是当斯格明子的尺寸能够小于10 nm后,就很有希望替代铁磁畴成为数字信息的载体.这就要在自旋轨道耦合更强的磁性材料中寻找更大的DM相互作用,或是运用四自旋相互作用等新的自旋耦合机制实现磁斯格明子[77].另外,如果能够实现斯格明子半导体材料,对斯格明子的调控就将增加一个新的维度.反铁磁中的斯格明子也是一个重要的方向[88−90],特别是面间反铁磁的人工结构中,可以通过调控铁磁的面间耦合来实现斯格明子的操控,如果能够实现体材料中的反铁磁斯格明子,就有可能实现太赫兹的斯格明子产生和翻转.

在可控单斯格明子的操控方面,低能耗低响应时间的斯格明子产生湮灭是研究的关键.现有的自旋转矩逻辑器件能够做到约100 fJ的能耗和亚纳秒的响应时间[147].磁斯格明子虽然具有拓扑稳定性,但也同时限制了其产生湮灭的可操作性.需要提出更多精妙的设计.

另外,现有得很大部分磁斯格明子研究是在薄膜或者准二维体系中完成的,这也和斯格明子的二维本质相一致,但是在三维体系中的斯格明子形态还有待确认.有研究表明,斯格明子在沿着磁场方向并不是简单堆叠,而是在靠近表面处形成了扭曲[148−150],而且从螺旋态到斯格明子态的相变过程中,还出现了磁单极子[151].断裂的斯格明子管道会形成一个磁单极子对,并在靠近表面处形成称为浮子(bobber)的新型拓扑结构[152−154].在有限厚度的手性磁体圆盘中,还会有靶状斯格明子的出现[66,155,156].这些初步的研究都表明,在三维中有更丰富的拓扑磁结构,它们的形成和动力学能够作为未来三维自旋电子学和类脑器件的铺垫.但是这些结构的实验表征方法目前仍旧欠缺,实现磁性三维再构的X光断层摄影术(tomography)已经在开发阶段,将来必定有更广阔的舞台[157,158].

从基础凝聚态物理的角度考量,磁斯格明子的研究并不是孤立的,它的本质是磁性材料中自旋轨道耦合的物理,所以它和很多领域内很多研究热点都有深刻的联系.中心反演和时间反演的双重破缺也是多铁材料的特征,因此绝缘的磁斯格明子材料也会显示出一定的电磁耦合,这已经在Cu2OSeO3材料中有报道[71],在其他复杂材料氧化物中的霍尔电导测量也显示出斯格明子存在的痕迹[159],它们电磁响应的研究是一个正在进行的方向.由于斯格明子在电流下的易移动性,通过电场控制斯格明子的产生或移动提供了用电场控制磁性的新的思路.强自旋轨道耦合还造就了一系列的拓扑绝缘体.磁性掺杂的拓扑绝缘体薄膜就会由于表面DM相互作用产生磁斯格明子[159],在M n掺杂的Bi2Te3中还由于DM作用强度对厚度的敏感性,磁斯格明子的产生湮灭可以通过厚度来调节[160].但是这些实验中的斯格明子都是通过霍尔输运的测量来间接证明,对磁构型的直接成像还没有实现,因此是由斯格明子或只是原子尺度的自旋倾斜而造成霍尔效应的机理还有待解释.强自旋轨道耦合在关联体系中还会诱导出一系列非中心对称的超导体[161],现已有实验报道对非中心对称超导体的磁性掺杂会形成斯格明子[75,162],超导体和斯格明子的相互影响还有待研究.

特别感谢中国科学院强磁场实验中心张裕恒院士、田明亮研究员和杜海峰研究员,中国科学院物理研究所韩秀峰研究员和于国强研究员,美国霍普金斯大学钱嘉陵教授以及加州大学洛杉矶分校王康隆教授的长期合作和讨论.