小陇山人工油松幼苗苗高生长研究

王 鹏，万 盼

(1.甘肃省小陇山林业实验局 林业科学研究所，甘肃 天水 741020；2.中国林业科学研究院 林业研究所，国家林业局林木培育重点实验室，北京 100091)

森林作为陆地生态系统的主体，为人类的生产和生活提供了各种产品和服务；然而，环境的恶化以及人类长期对森林资源不合理的开发利用，导致森林面积急剧下降，尤其是天然林资源不断缩减[1]。因此，亟需对森林资源进行维持和保育。保护天然林、发展人工林，是当今林业提倡的一种发展模式[2-3]。油松(Pinustabulaeformis)具有耐低温、干旱和贫瘠的特点，是我国北方温性针叶林中分布最广的森林群落，也是我国北方广大地区最主要的造林树种之一[4-5]。小陇山自然保护区是我国暖温带-亚热带过渡地带，近年来油松人工林的发展比较迅速[6]。因此，建立油松生长模型，有利于研究其生长规律，对实现油松人工林培育及其资源的优化配置有重要意义。

理论生长方程具有良好的理论解释基础和模拟性能，已被广泛应用到林木生长模型的研究领域中[7]。目前，应用较多的方程主要有：理查德、坎派兹、高斯、舒马赫等模型方程[8]；其中，理查德(Richards)和舒马赫(Schumacher)理论方程被常用于建立树高生长模型[8-10]。理论差分方程是利用不同时点模型方程参数不变的特性，使用差分法将理论方程中的参数消去，达到消元的目的，进而得到相应的理论差分表达形式[11]。差分方程能很好地适应基于生长间隔数据的树高模型，可以很好地模拟林木的生长进程[12]。目前，有关油松生长模型的研究，主要是侧重利用理论方程来建立其生长模型，但这局限于对油松整体生长了解，无法深入了解其生长进程。对此，本研究以甘肃小陇山林区的油松苗为对象，通过常用的2种理论方程得出其相应的差分方程，来建立油松苗高的生长模型，进而掌握其生长进程，为科学经营小陇山油松人工林奠定基础。

1 研究区概况

小陇山林区位于甘肃省东南部(33°30′-34°49′N，104°22′-105°43′E)，地处秦岭西段，平均海拔1 600 m，最高海拔2 686 m，属暖温带向北亚热带过渡地带，兼有我国南北气候特点，大多数地域属暖温湿润—中温半湿润大陆性季风气候。年平均气温7～12℃，极端最高气温39.2℃，极端最低气温-23.2℃，年降水600～900 mm，主要集中于7-9月，年蒸发989～1 658 mm，相对湿度68%～78%，年日照时1 520～2 313 h，无霜期130～220 d，区内秦岭以北的地带性土壤为灰褐土，以南为黄褐土，垂直分布比较明显[13]。

2 研究方法

2.1 苗高生长预测模型

在所研究的试验田内，选择640株移栽后生长了3 a的油松苗(生长时间是按照容器苗移栽到大田后的时间)，测定每株的苗高，包括第1、第2、第3年的苗高；其中400株用于建立模型，240株用于检验模型；大田基本情况为：海拔约为1 365 m，坡度大约为12°～4°，坡向为西南。具体方法为：利用差分途径得出不同的理论差分方程模型，通过回归分析，求出其相应参数，选出油松苗高生长的最优模型；同时，将标准样地调查的数据与模型预测的理论值进行比较，进而验证模型的精确性。

2.1.1 数学模型 采用理查德(Richards)和舒马赫(Schumacher)理论生长模型描述：

1)理查德(Richards)生长模型：

H=a(1-e-bt)c

(1)

式中，H为苗高(m)；t为苗龄(a)；a、b、c为模型参数。

对于不同年龄的苗高，通过差分方程途径，即利用不同时点方程参数不变性的特点，消去尺度参数，进而导出不同年龄苗高之间关系的生长方程[10]。

消去尺度参数a,由式(1)得到式(2)：

(2)

式中，H(t+1)、H(t)分别是苗龄为t+1、t苗高(m)；b、c为模型参数。

消去形状参数c,由式(1)得到式(3)：

(3)

式中，H(t+1)、H(t)分别是苗龄为t+1、t苗高(m)；a、b为模型参数。

2)舒马赫生长模型(Schumacher)：

(4)

式中，H为苗高(m)；t为苗龄(a)；a、b为模型参数。

采用上述差分方程途径，消去参数。

消去尺度参数a,由式(4)得到式(5)：

(5)

式中，H(t+1)、H(t)分别是苗龄为t+1、t苗高(m)；b为模型参数。

消去尺度参数b,由式(4)得到式(6)：

(6)

2.1.2 模型验证 采用均方根误差(RMSE)和相对平均绝对误差(RMAE)作为模型评价的指标，并求出模型的预估精度(P)：

(7)

(8)

(9)

式中，N为所测油松幼苗株数；Pi为第i株幼苗株高的预测值；Oi为第i株幼苗株高的实测值。RMSE是对预测值与实测值偏差的总体估计，用来定量描述预测值与实测值的一致性；RMSE值越小，表明模拟结果越接近于实测值；RMAE值在0到1之间，表示实测值与模拟值之间的吻合从“最优”到“最差”；t0.05是置信水平为a=0.05时的t分布临界值，f为模型的参数个数。

2.2 油松苗生长地土壤采集和分析

在油松苗生长地(大田)设置3个小区，3个小区位置分别位于上、中和下坡，坡度大约为12°～4°，坡向为西南；在每个小区内设置5个点，用土钻取每个点的表层(0～10 cm)土样，带回实验室进行养分分析。土壤养分测定参见土壤农业化学分析方法[14]。

2.3 数据处理

用Excel 2010进行数据整理，将最近2 a(第3年和第2年)的生长数据用式(2)、式(3)、式(5)和式(6)模型进行拟合，通过1Stopt软件进行非线性回归分析，选出最优模型；并通过Excel计算均方根误差(RMSE)和相对平均绝对误差(RMAE)，检验模型的精确性。通过SPSS分析土壤养分含量与苗高的相关性。

3 结果与分析

3.1 油松人工苗生长规律分析

分别对苗高的总生长量、连年生长量和年平均生长量计算，并依次绘制油松苗高生长曲线(图1)。由图1可知，油松苗苗高生长量与时间成正相关。经分析，幼苗的总生长量、连年生长量和年平均生长量与时间拟合的决定系数(R2)分别为0.938、0.792和0.784，结果表明，油松苗生长良好，用于高生长模型建立选取的数据合理。

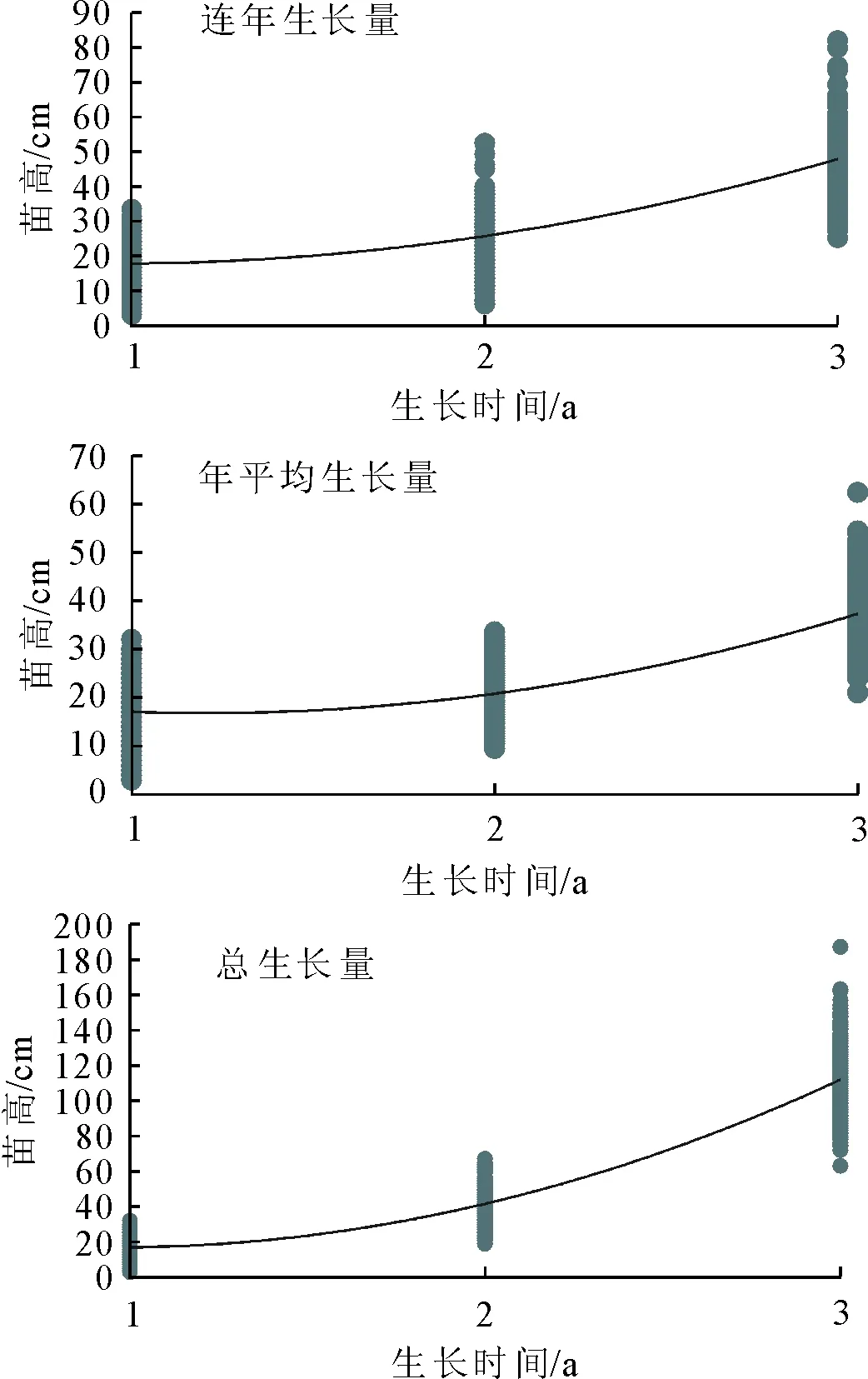
图1 油松苗生长过程Fig.1 Height growth of Pinus tabulaeformis seedlings

3.2 生长模型的建立

由表1可知，4种模型的相关系数和决定系数基本相同，残差平方和却相差很大；其中，式(3)和式(6)的残差平方和均较小。最优模型应该为决定系数最大且残差平方和最小的拟合模型；因此，式(6)可作为油松苗高生长的最佳模型：

(10)

3.3 模型的验证

将第2年油松幼苗苗高数据分别代入式(2)、式(3)、式(5)和式(6)相应的模型中，计算出第3年苗高的预测值。由表2可知，式(6)模型的均方根误差(RMSE)和相对平均绝对误差(RMAE)均最小，分别为0.083 73、0.058 26，这进一步说明了该模型为最佳模型；经计算，该模型预估精度高达99.20%，适用油松苗的生长预测。同时，将样地调查得到的实测值与预测值进行比较(图2)，可以看出，虽然某些点的预测值与实测值之间存在较大偏差，但整体来看，两者相差不大，模型效果较好，R2=0.835。

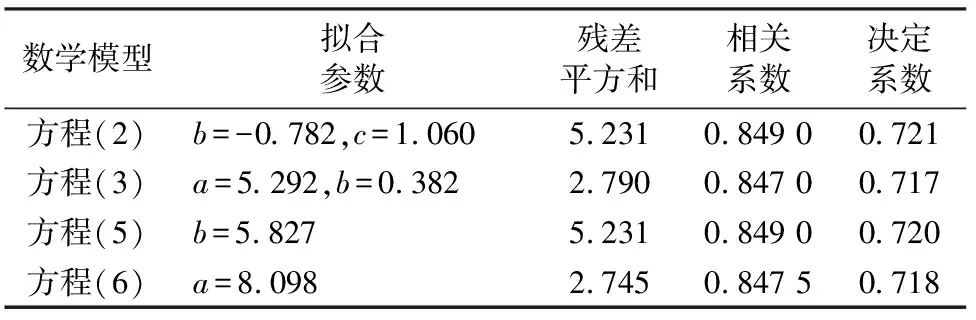
表1 油松苗苗高生长数学模型拟合参数Table 1 Height growth mathematical model fitting parameters of P.tabulaeformis seedlings

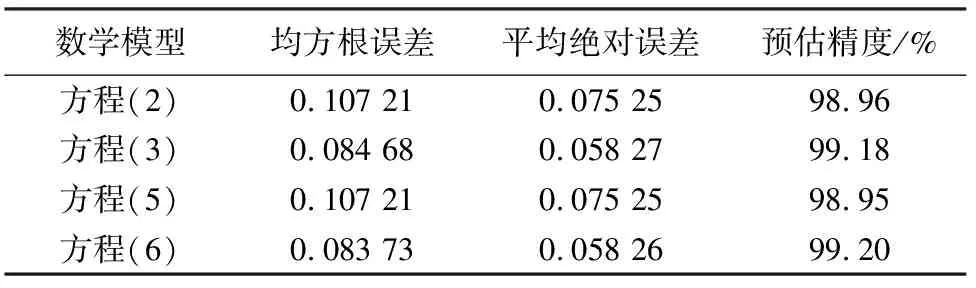
表2 油松苗苗高生长数学模型验证参数Table 2 Height growth mathematical model validation parameters of P.tabulaeformis seedlings

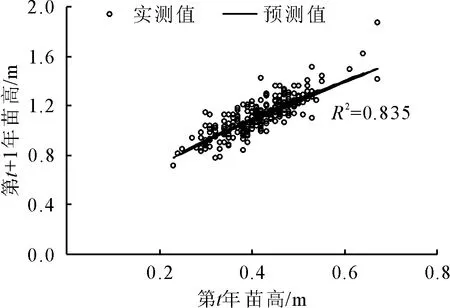
图2 预测值和实测值的对比Fig.2 Comparison of the simulated value (line) and the measured value (circle)

3.4 苗高与土壤性质相关分析

苗高生长是环境因子与植物生理过程综合作用结果。土壤养分能够影响苗木高生长，为了了解土壤养分因子与油松苗高生长的相关性，利用SPSS软件进行分析。从表3可以看出，油松幼苗苗高与土壤全K、碱解N、速效K含量和pH均无显著相关，而与土壤有机质、全N、全P和有效P含量呈现正相关。可见，土壤中有机质、全N、全P和有效P含量均可以显著影响油松幼苗苗高生长。

4 结论与讨论

利用2个常用的理论生长方程，通过消除尺度参数，得出相应的差分方程，并用油松幼苗的第1、第2、第3年的苗高的实际数据进行拟合，进而得出不同年龄苗高之间关系的生长方程，该方程能很好地适应基于生长间隔数据的树高模型，可以很好地模拟林木的生长进程。同时，通过分析拟合方程的相关指数、决定系数以及预测精度，以此比较不同拟合方程的优越性，最终选择出较优的模型，所采用的分析方法和得到的结论仅供参考和讨论。

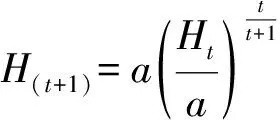
研究表明，油松生长与土壤养分含量之间相关性较高[15-17]。本研究测定了油松苗生长地表层土壤养分含量，并分析养分含量与油松幼苗苗高的相关性，这对油松幼苗的经营和管理具有重要意义。研究表明，表层土壤中有机质、全N、全P和有效P含量与油松幼苗苗高呈正相关性，说明有机质、全N、全P和有效P含量对油松幼苗高生长有较大的影响，这与其他研究结果相符[18-19]。可能是由于油松幼苗在苗高生长期对氮素和磷素需求量比较大的缘故，因此在油松幼苗生长过程中应该注重有机N肥和P肥的补充。

表3 苗高与土壤因子的相关性Table 3 Correlation coefficient between height and soil factor of P.tabulaeformis seedlings

注:*P<0.05。