原型水泵水轮机在泵工况驼峰特性研究

王驰航，郭志伟

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

0 引 言

水泵水轮机是抽水蓄能技术的核心，随着科技的不断发展，其单机容量越来越大，水头、转速越来越高；效率也将赶上常规水泵、水轮机[1]。与常规机组相比，抽水蓄能机组具有工况多且变换复杂，工况转换频繁且快速等特性，这就使得水泵水轮机的稳定性与可靠性问题更加突出，其重要性甚至超过了机组效率[2]。因此国内外对水泵水轮机的主要研究集中在“驼峰”区和“S”区运行机理与稳定性问题上。驼峰区水泵工况启动作为抽水蓄能电站过渡过程研究的最重要组成部分，对驼峰区稳定性问题的研究具有重要意义。

迄今为止，国外关于水泵水轮机泵工况驼峰区内部流动的研究还比较少。其中以试验研究为主，通过多种测试手段对驼峰区内部流场进行测试分析。如Gabriel Danciocan[3]等人利用LDV和PIV技术，得到了正斜率区内活动导叶之间速度场分布情况，观察到了瞬态的双列叶栅流道速度分布。J Yan[4]等人采用可压缩计算模型，在无叶区得到了与试验相似的压力脉动。Yang[5]等通过试验对多级水泵水轮机的驼峰特性进行研究，观察到驼峰区内扩压叶栅流道瞬态流态分布。张兰金[6]等对转轮的内部流速分布、涡分布和叶片压力分布进行了分析研究。王焕茂[7,8]等应用RNGk-ε湍流模型对水轮机水泵工况进行了全通道数值模拟，并采用速度三角形分析了驼峰特性形成的原因,虽然模拟性能曲线的总体趋势与试验数据相同，但是峰值点的流量位置与试验相差较大。姚志民[9]等在泵工况下对无叶区流场和直锥段流场进行了测量研究，并认为带直锥段的尾水管可以改善泵工况时进口处的流动特性。舒峻峰[10]采用数值模拟方法对驼峰区进行了深入研究，详细分析了不同开口不同部件的水力损失和流动特性。

虽然前人在水泵工况“驼峰区”的稳定问题上做了大量的深入研究，但是大部分都是通过对模型泵进行数值模拟来分析水泵水轮机内部的流场变化，尽管模型泵与原型泵在外特性，如扬程，出力，效率上存在一定的比尺效应，但这并不能说明模型泵与原型泵的内特性也存在着相似的关系。所以为了得到更为准确的内部流场变化规律，本文对原型水泵水轮机驼峰工况进行了全流道定常数值计算，并在此基础上对原型泵驼峰区内的流场特征进行了分析和研究。同时发现旋度场也可以反映原型水泵水轮机泵工况下内部流动涡的运动变化规律。

1 湍流模型与边界条件

数值模拟选用SSTk-ω模型封闭方程。SSTk-ω模型综合了k-ω模型和k-ε模型的优点，对边界层内的低雷诺数流动采用k-ω模型，对边界层外部充分发展湍流区采用k-ε模型，SSTk-ω模型对于分离流具有很好的适应性。

尾水管进口和蜗壳出口分别为水泵水轮机泵工况的进口边界和出口边界。本文数值模拟计算边界条件采用质量流量进口和压力出口。尾水管进口流道规则(类似圆管)，取水流方向垂直于尾水管进口，压力出口取一个大气压强。

2 研究对象和计算网格

研究对象为某抽水蓄能电站水泵水轮机，为立轴单级的混流式水泵水轮机。原型水泵水轮机工况水头为 195 m， 水轮机工况额定功率为306 MW，水泵工况额定转速为 250 r/min，额定频率为50 Hz，最大静水头为 217 m，最小静水头为187 m。图1为水泵水轮机三维模型，计算区域包括蜗壳、固定导叶、活动导叶、转轮和尾水管5个部分。原型机为9叶片水泵水轮机，有20个固定导叶、20个活动导叶，转轮进出口直径为0.44 m和0.30 m，导叶高度为 66.72 mm，导叶分布圆直径为0.52 m。

比转数是衡量水利机组性能的重要参数，其计算公式是在相似定律的条件下推导得出的，满足水泵水轮机几何相似和运动相似，对于泵工况，比转数定义为：

(1)

式中：n为水泵水轮机额定转速；Q为水泵水轮机泵工况额定流量；H为水泵水轮机设计水头。

计算比转速结果为46.0，按比转数分类，该模型属于中低比转数类型装置。

图1 原型水泵水轮机三维图Fig.1 3D drawing of prototype pump turbine

如图2所示，整个计算区域都采用结构化的六面体网格。其中蜗壳网格单元数约为132万，活动导叶网格单元数约为206万，固定导叶网格单元数约为155万，转轮网格单元数约为261万，尾水管网格单元数约为183万，总网格单元数约为937万。

图2 不同部件计算网格Fig.2 Calculation mesh with different parts

3 计算结果与分析

3.1 网格无关性验证

网格节点数对计算效率和计算精度有较大的影响，一般来说网格密度越大，计算精度往往越高，但计算所占用的资源和时间也会越长。因此，需要采用不同网格密度对同一工况进行数值模拟，并通过与试验值对比验证其准确性。表1中列出了进行网格无关性验证的5套网格。

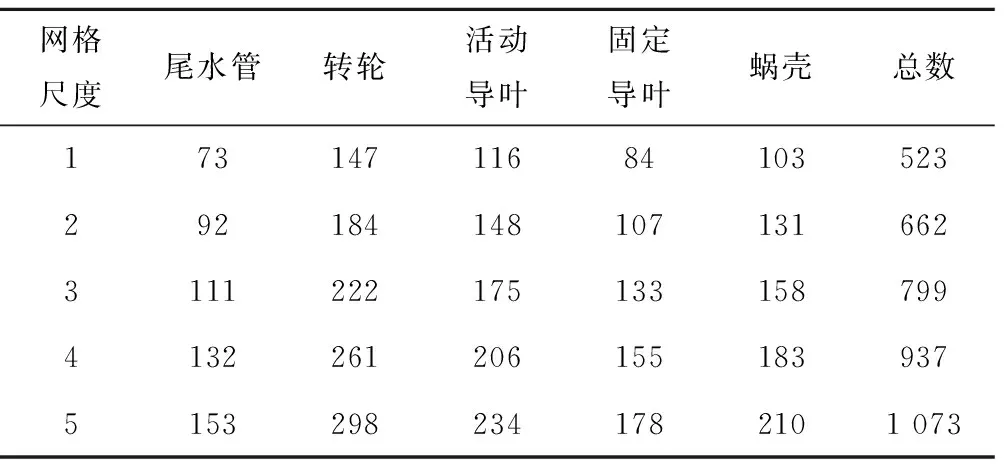
表1 计算域各部分的网格单元数 万

试验结果是通过物理实验的手段获得。试验在水泵水轮机转速1 500 r/min时进行，在正常运行范围内，对13个不同导叶开度工况进行了试验，其中最小开度为3°，最大开度为30.5°。最终通过选取最高效率点的试验数据与原型机组的数据对比得出原型机组与模型机组扬程、效率、轴功率等外特性参数的关系。试验的水泵水轮机模型是将安装在TP3装置台上的白莲河抽水蓄能原型机组按1:11.9的比例缩放设计而成。试验台的测量误差经计算为±0.2%。

由图3所示，当网格数较小时，数值模拟的结果波动较大，网格节点数对计算结果影响较大，当网格增大到到937万时，随着网格数的继续增加，数值模拟的结果趋于平缓，变化较小，网格密度对计算结果影响越来越小，同时网格为937万时数值模拟出的结果相对误差为1.25%，在误差范围允许内，综合计算精度和计算时长考虑，选择第四套网格进行数值模拟。

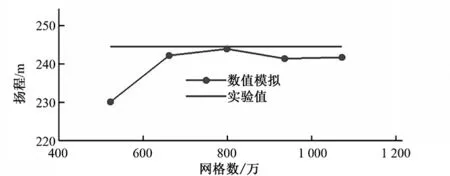
图3 网格无关性验证Fig.3 The validation of mesh independence

3.2 计算结果验证

通过分析试验数据发现活动导叶开度为15°时，现场测量的工况点更多，数据更加准确可靠，且扬程-流量曲线的驼峰区更加明显，便于观测到更真实可靠的驼峰区内流场的模拟结果。所以选择此开度，对原型泵试验的24个工况点进行数值计算。

从图4给出了泵工况外特性曲线看出，计算曲线与试验曲线的变化趋势基本一致，吻合度较高。最优效率点对应的流量为QBEP=112.2 m3/s，在扬程-流量曲线中，0.8～0.85QBEP区域存在明显的驼峰现象，且误差不超过2%，但偏离最优效率工况点，超负荷区的误差较大。效率-流量曲线中，最大误差不超过5%，效率先随着流量的增大而增大，在设计流量处到达最大值后随着流量的增大而减小，流量偏离设计工况越远，效率下降的越快。轴功率-流量曲线的最大误差不超过3%，并且随着流量的增大，误差逐渐减小。

图4 原型水泵水轮机水泵工况的外特性Fig.4 External characteristic curve of prototype pump turbine

李德友[11]等采用不同的湍流模型对水泵水轮机水泵工况进行了数值模拟，发现对于低负荷区和驼峰区SSTk-ω湍流模型的计算结果与试验更为接近，但在超负荷区域的误差较大。通过对比，计算结果和试验结果吻合较好，尤其是对驼峰位置的捕捉较为精准，计算误差控制在可接受的范围内，表明数值模拟与试验结果反映的规律基本一致，计算结果可靠，可作为驼峰特性研究分析的依据。

3.3 流线分布特性

图5给出了中间截面的流线分布特性，从图5中可以看到驼峰区流场变化规律十分复杂。在最优工况时，叶轮压力面侧的速度明显小于吸力面侧的速度，叶片进口压力面侧出现扁平的低速区，但叶轮区域的速度分布均匀对称，流动状态较好。隔舌附近活动导叶压力面和固定导叶吸力面之间的流道内流体介质的运动状态变得恶劣，出现了漩涡。在驼峰极大值工况点处(Q=0.85QBEP)，固定导叶单流道的漩涡范围增大，出现漩涡的流道数增加。随着流量的继续减小，在驼峰极小值工况点处，双列叶栅绝大多数流道压力面和吸力面侧被低速区包围，低速区的流体形成漩涡，漩涡范围扩大，堵塞流道，使得整个双列叶栅内的流动环境恶劣，能量大量消耗在双列叶栅内，流动损失增大，水泵水轮机做功效率降低，在小流量低负荷区时，靠近隔舌区双列叶栅低速区的范围更大，流道内的漩涡更多，而远离隔舌处部分区域的漩涡范围有所减小。蜗壳区的低速带随着流量的减小而增大，流线曲率变化越来越大，介质流动状态越来越恶劣。而且流场受双列叶栅区域的影响较大，双列叶栅区域形成的漩涡运动影响了蜗壳流体的运动状态，增加其内部的流动损失。

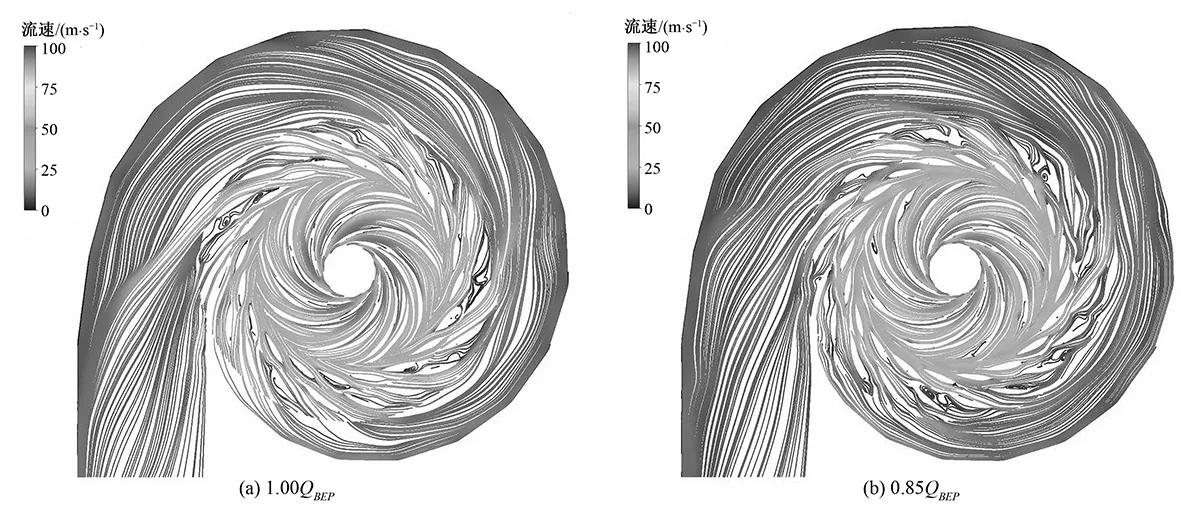
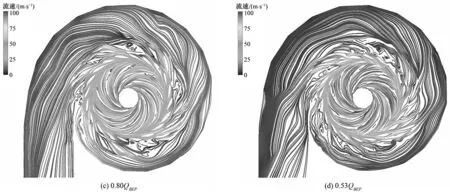
图5 中间截面流线变化特性Fig.5 The change of steamline on the midspan

3.4 涡量变化特性

图6给出了中间截面的涡量变化特性，从图6中可以看到，在刚进入驼峰区时，涡集中分布在少数活动导叶和固定导叶之间的流道内，而随着流量减小，涡逐渐充满了整个双列叶栅流道，水泵水轮机的流动状态变得恶劣，流动损失增大，做功效率降低，在驼峰极小值工况点处，涡主要分布在隔舌区附近，而进入小流量的低负荷区后，涡集中分布在叶轮出口和活动导叶进口的流道内，且分布范围更大。从最优工况到小流量低负荷工况，随着流量的减小，水泵水轮机内部介质的流态越来越恶劣，做功的效率越来越低，与实验模拟的效率-流量曲线的变化规律一致。

图6 中间截面涡量变化特性Fig.6 The change of vorticity on the midspan

3.5 旋度场变化特性

陶然[12]等在试验的基础上采用非定常分离涡模拟(DES)的方法，得到随着流量的减小，驼峰区内的能量损失50%左右集中在活动导叶区，固定导叶区次之。由流线场可以看到进入驼峰区时，固定导叶流态恶劣的区域在隔舌附近，所以如图7选取靠近隔舌区的双列叶栅进行观察，分析其流场的变化规律。

图8给出了不同流量下靠近隔舌区双列叶栅剖面图的旋度场分布，由于流量的不同，旋度较强的区域分布的位置也不同，在设计工况处，强旋度区域主要集中在活动导叶压力面和固定导叶压力面，随着流量的减小强旋度区域从活动导叶压力面向固定导叶上冠区的吸力面扩散，但固定导叶和叶轮出口处的强旋度区域范围减小，在驼峰区极小值工况点处，强旋度区域的范围从双列叶栅流道扩大到了叶轮区，流动状态十分恶劣，能量大量消耗在双列叶栅和叶轮区。当进入小流量低负荷区时，强旋度区域主要集中在叶轮出口和活动导叶进口之间的流道内。

图7 靠近特殊导叶双列叶栅剖面图Fig.7 The profile of tandem cascade near the special blade

图9给出了中间截面的旋度分布特性，在设计工况处，活动导叶压力面处的旋度强度较大，该处的介质流动状态恶劣，进入驼峰区后，少数活动导叶与固定导叶之间的流道和部分叶轮出口处的旋度强度较大，当流量继续减小到达扬程极小值工况点时，流态恶劣范围扩大，双列叶栅整个流道内都出现了旋度较强区，能量损失增大，同时隔舌区流态的恶化也影响了蜗壳内流体的运动。进入小流量低负荷区后，流道内强旋度区范围更大且更集中在叶轮出口。从设计工况进入驼峰区后，随着流量的减小，强旋度区越来越大，介质的流动状态越来越恶劣，水泵水轮机的做功功率越来越低，与实验模拟的效率-流量变化规律一致。

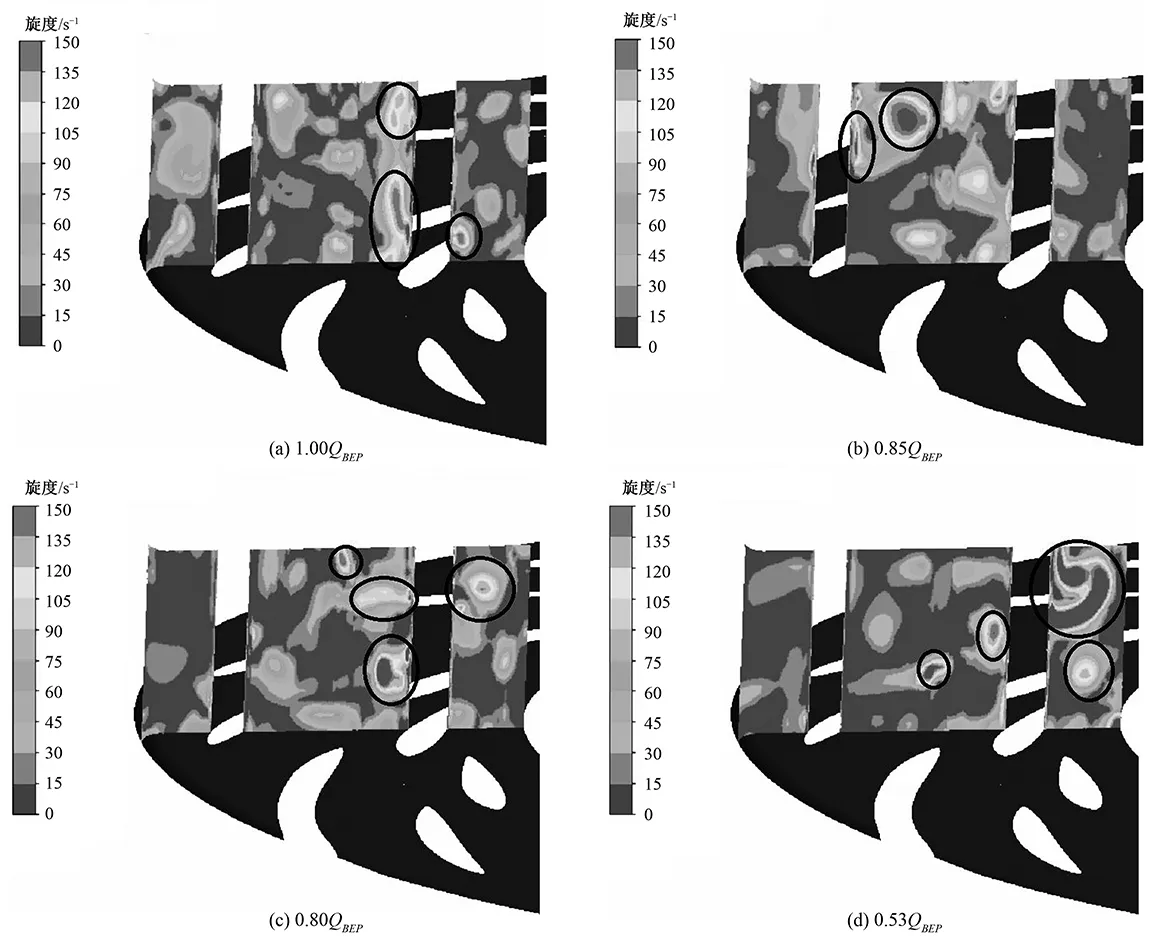
图8 靠近特殊导叶双列叶栅剖面图旋度场Fig.8 The swirling strength of tandem cascade near the special blade

图9 中间截面旋度场变化Fig.9 The change of swirling strength on the midspan

4 结 语

为了研究水泵水轮机驼峰区内部的流场变化规律，在活动导叶为15°开度下，对原型水泵水轮机在泵工况下的三维定常湍流进行数值模拟。结合实验数据，在验证计算结果的可靠性之后，得到了如下结论。

(1)原型水泵水轮机由设计工况进入驼峰区后，双列叶栅部分固定导叶和活动导叶流道被低速区流体包围形成漩涡，随着流量的减小，不断向周围流道扩散，能量损失增大，做功效率降低。

(2)通过观察中间截面的涡量场，发现随着流量减小，水泵水轮机内部的流态越来越恶劣，做功效率逐渐降低，在驼峰极小值工况处，涡主要分布在隔舌区附近，而进入小流量低负荷区后，涡集中分布在叶轮出口和活动导叶进口，且分布范围更大。

(3)通过观察整个流道以及隔舌区附近双列叶栅的旋度场，发现不同工况下，旋度较大的区域分布的位置也不同。在驼峰极小值工况处，强旋度区集中在整个双列叶栅，在小流量低负荷区，强旋度区主要集中在叶轮出口和活动导叶进口。