泵站进水池自由表面漩涡研究
王自明,王月华,韩晓维,叶 龙
(浙江省水利河口研究院,杭州 310020)
0 引 言
泵站进水口形成的漩涡,一般分为自由表面漩涡、水中漩涡两种,其中自由表面漩涡对工程影响较大,会导致泵站进口有效过水断面的减小,降低过流能力,由于挟入空气,水流不稳定性加强,加剧了水流脉动,从而增加了脉动压力幅度并可能引起振动或建筑物表面的空蚀[1],因而通常是关注的重点。然而泵站进口是否会发生吸气漩涡是工程设计中的难题,目前一般通过临界淹没深度进行估算,此外泵站整体水工模型也是研究泵站运行的重要手段,一般水工模型满足重力相似并保证几何相似,但在进行泵站漩涡模拟时雷诺数Re及韦伯数We往往达不到临界值的要求[2],造成模型的黏滞力及表面张力的影响不可忽略,从而造成了模型试验的失真即“缩尺效应”。因此为了克服缩尺效应的影响,一般认为采取不同比尺的系列模型[2]、增加模型流量[3]等流速准则[4]等可消除缩尺效应的影响,在实际操作中出于成本的考虑往往采用增加模型流量的方法,但对于不同的缩尺模型,流量增加到多少合适,目前尚无定论。
本文通过典型泵站,对泵站进口淹没深度和淹没弗劳德数的经验公式进行探讨,并通过模型试验对探讨结果进行试验验证。
1 工程概况
某枢纽工程为减轻大洪水时下游防洪压力,设有5台立式轴流泵的排水泵站,将内河侧洪水排向外江,单泵流量33 m3/s,每台泵进口流道为1孔,每孔5.4 m×7.5 m(高×宽),进水前池底板高程-6.3 m,泵站最低运行水位3 m;同时为满足引水需求,设有2台竖井式贯流泵引水泵站,将外江水引入内河侧,单泵流量20 m3/s,每台泵进口流道为1孔,每孔4.1 m×7.4 m(高×宽),进水前池底板高程-2.5 m,泵站最低运行水位3.3 m。其平剖面图如图1。

图1 排水泵站、引水泵站平剖面图(单位:长度mm;高程m)
2 自由表面漩涡
2.1 漩涡的分类
美国 Alden 实验研究室根据实验观察到的现象对漩涡进行分类,将表面漩涡依其强弱分为以下六种类型 (Hecker,1987,表1)。漩涡对工程产生的影响因其类型而异,如表中1和2型近于无漩涡,不会引起危害,允许存在;3和4型为弱漩涡,对机组与建筑物会产生一定影响,但危害一般不严重,宜考虑防止出现;5和6型属于强漩涡,可能引起较严重的后果,工程中通常要避免出现。

表1 漩涡分类
2.2 临界淹没深度及淹没弗劳德数
判别进水口是否会产生漩涡,前人进行了大量基础性实验,取得了许多重要的研究成果。为了避免发生自由表面吸气漩涡并降低水中涡带来的漩流,进水口必须有足够的淹没深度H/D(H为进水口底板以上水深,D为进水口高度),因此在进水池设计时,一般应估算出相应的临界淹没深度,根据水电站进水口设计规范中采用戈登公式s=cvd1/2计算可知排水时s=1.04 m,引水时s=0.74 m。而本工程中排水口和引水进口淹没深度分别为:3.9 m和4.9 m满足规范中淹没深度的要求。除临界淹没深度H/D的影响外, Lewellen[5]认为进水口弗劳德数Fr也是影响漩涡形成的重要因素 ,因此也有人通过计算进水口淹没弗劳德数(Frs)来判别泵站进口是否会发生进气漩涡。目前较为流行适用于含有流道的进水池漩涡进行判别标准有如下几种(表2)。
(1)美国水泵进水口设计标准[6](ANSI/HI,1998)中推荐采用Hecker提出的最小淹没深度计算公式:H/D=1+2.3Fr。
(2)南京水利科学研究院胡去劣[7]在研究低弗劳德数进口漩涡特性后则认为:①无漩涡的临界弗劳德数Fr=0.15。当进口弗劳德数小于该临界值时,不论进口淹没度大小均无漩涡发生。②存在偶发性串通漩涡区的临界弗劳德数Fr=0.19。当进口弗劳德数小于该临界值时,不会发生偶发性串通漩涡。③进口弗劳德数大于0.19后, 无涡的临界相对淹没度H/D=2.7Fr0.35,0.15 (3)印度水电中心研究所则建立了进口弗劳德数(Fr)和淹没弗劳德数(Frs)之间的相互关系,并建议以此作为预测原型进水口是否发生吸气漩涡的判别式。 Frs≤0.5Fr+0.08;Frs=v/(gSm)0.5 式中:v为进水口管道水流流速;Sm为进水口管道中心线以上水深。 (4)Pennino[2]等则认为当进水口淹没弗劳德数Frs小于0.23,就不易出现吸气漩涡。 本工程排水泵站最小淹没深度H=3+6.3=9.3 m;相对淹没深度H/D=9.3/5.4=1.72,进口弗劳德数Fr=0.09;淹没弗劳德数Frs=0.10。引水泵站最小淹没深度H=3.3+2.5=5.8 m;相对淹没深度H/D=5.8/4.1=1.4,进口弗劳德数Fr=0.09;淹没弗劳德数Frs=0.11。 表2 本工程是否发生吸气漩涡的判别情况 综上所述,无论是排水泵站还是引水泵站,按照各家的判别标准,判别结果基本一致:排水泵站及引水泵站进水池均不会发生吸气漩涡。 为研究泵站进水池可能产生的漩涡类型,对排水、引水泵站进行了整体水工模型试验。采用正态模型,模型比尺为1∶35,按重力相似准则设计,以保证水流运动相似、动力相似,模型包含了上游连接段、泵站进口段、泵站、出口段以及外江等,模型全长约35.0 m。上游河道、泵站枢纽、外江等按设计图纸及实际地形控制放样,其中模型上游河道、进水池等以断面板定位、水泥砂浆抹制,引水泵站、排水泵站以有机玻璃制作,其糙率为0.009,原型混凝土抹面糙率为0.011~0.017,按照相似比尺计算出原型糙率为0.016,因此采用有机玻璃模拟能满足糙率相似要求。 泵站工程临界淹没深度以及淹没弗劳德数的计算可以判断该泵站工程不会发生吸气漩涡,为进一步对泵站进水池是否会发生吸气漩涡进行论证,以1∶35的比尺对泵站进行整体水工模型验证。为避免缩尺效应,当前通用的漩涡模型的相似设计方法是:按弗劳德准则予以模拟,模型雷诺数值大于3×104,韦伯数大于等于120,使黏滞力和表面张力的影响处于次要位置,当雷诺数和韦伯数低于上述两个值时,可在试验过程中适当增加流量或流速,以避免缩尺效应。一般根据以下公式: (1)Amphlett,M.B[3]提出,模型雷诺数Re应满足: Re=Q/υs>3×104 式中:Q为流量;υ为运动黏滞系数;s为孔口中心淹没深度。 (2)Jain.A.K[8]提出,模型韦伯数We应满足: We=ρv2d/σ≥120 式中:v为孔口平均流速;ρ为液体密度;d为孔口高度;σ为液体表面张力系数。 此外,根据日本TJS Turbo Association 标准2005年版则采用增大Froude以预测和观察漩涡。在日本TJS标准中,自由表面涡相似条件为: 相应模型参数的比尺为: 计算该泵站模型雷诺数Re及韦伯数We,排水泵站模型泵站进口雷诺数约为2.12×104,模型韦伯数约为39,引水泵站模型泵站进口雷诺数约为2.26×104,模型韦伯数约为19。排水、引水泵站进口的雷诺数值均小于3×104,韦伯数均小于120。需要增加模型流量以消除模型的缩尺效应。经Amphlett.M.B及Jain.A.K公式计算可知,当排水泵站单台水泵流量增加到2倍时排水泵站可避免缩尺效应,此时雷诺数约为4.2×104,韦伯数约为159。当引水泵站单台水泵流量增加到2.5倍时,引水泵站进口可避免缩尺效应,此时引水泵站雷诺数约为3.5×104,韦伯数约为159。而按照日本TJSTurboAssociation标准自由表面涡模拟相似条件公式计算可知,为避免缩尺效应取比尺(本模型λL为35)的0.3次方,即需要加大2.9倍流量可避免缩尺效应。 经综合比较分析,为了解本工程泵站进口的真实漩涡情况,本次模型试验采用加大2.9倍流量以避免缩尺效应。 将流量加大2.9倍后,排水泵站进口表面波动、凹陷明显,但仍然没有观测到漏斗型的吸气漩涡出现,但阵发性表面下陷较为明显,对比表1,属于3~4型漩涡;引水泵站进口与排水泵站进口类似,其表面波动、凹陷明显,但仍然没有观测到漏斗型的吸气漩涡出现,对比表1,属于3~4型漩涡。此结果与临界淹没深度以及淹没弗劳德数对泵站进口是否发生进气漩涡的判断是基本一致的。但是仍有可能发生3~4型弱漩涡,宜考虑防止出现。因此认为泵站进口是否发生漩涡以及发生漩涡的程度,除需对临界淹没深度和淹没弗劳德数进行计算外还有必要对泵站是否产生漩涡进行物理模型试验的验证分析。 本文通过对泵站进口的临界淹没深度及淹没弗劳德数的计算得出,泵站工程的排水泵站及饮水泵站均不会出现吸气漩涡,并且通过水工模型试验对进行了验证,结果表明临界淹没深度及淹没弗劳德数对泵站进口是否出现吸气漩涡的判断是基本可信的。但水工模型试验表明泵站进口仍然可能出现3~4型弱漩涡,其对机组与建筑物的影响虽然小于吸气漩涡但仍会对泵站的运行产生一定影响,宜考虑防止出现,因此在类似的工程中除进行临界淹没深度的计算外还有必要对泵站是否产生漩涡进行物理模型试验的验证分析。此外本文中所采用的避免缩尺效应的几种方法也可为同类型的物理模型试验提供一定的借鉴。
3 试验研究
3.1 缩尺效应
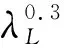
3.2 成果分析
4 结 语

