竖井贯流泵装置水力特性的数模分析

陈加琦，苏志敏，王梦成，濮菊琪，陈松山

(1.昆明理工大学电力工程学院，昆明 650504；2.扬州大学水利与能源动力工程学院，江苏 扬州 225127)

0 引 言

竖井贯流泵站竖井为开敞式，电机、齿轮箱和推力轴承箱置于竖井内，采光、通风和防潮条件良好，运行和维护方便。机组卧式安装，水流从进水池流经竖井进水流道、水泵和出水流道至出水池无竖直调向，水平方向直进直出，水力性能好，水泵装置效率高。结构简单、开挖深度小，工程投资省。近十多年来在国内低扬程大型泵站中得到广泛应用。

竖井贯流泵站最早被成功应用于江苏太湖流域的低扬程排涝泵站-裴家圩泵站和梅梁湖泵站[1,2]。此后，在江苏和广东相继建成一批竖井贯流泵站，例如江苏的江尖泵站、澹台湖泵站、张家港枢纽泵站、串新河泵站、运河东枢纽泵站、走马塘泵站、横塘河泵站、大渲河泵站、邳州泵站、井头泵站等；广东的黄麻涌泵站、沙坪泵站、大岸泵站等。近年来，竖井贯流泵站在海河流域、杭嘉湖流域、宁波三江流域及一些区域性排涝工程和城市防洪工程中的正得到大力推广应用。目前最大水泵单机流量已达50 m3/s，叶轮直径3.95 m。

伴随着竖井贯流泵站建设的需求，国内研究者分别结合特定工程，主要利用数值模拟和水泵装置模型开展竖井流道研究。郑源[3]结合江苏梅梁湖竖井贯流泵站，试验测试了在相同进、出水流道情况下两种不同转轮的水泵装置能量特性。陈松山[4,5]数模优化了毛漾荡、江尖、沙坪等泵站竖井流道型线，提出规则化设计方法，并模型试验验证了水泵装置性能；龙凤华等[6]整体数模比较广东深圳沙井泵站3种不同泵装置方案，提出了一种进出水流道优化设计方法，并得到了水泵装置模型试验验证。朱红耕等[7]为江苏步凤河南闸站设计了一种竖井流道进水、虹吸流道出水的新型竖井贯流泵装置，数模分析进、出水流道流动特性，并预测水泵装置性能。陆伟刚[8]试验测试了江苏大运河东竖井泵站不同叶片角度下的泵装置能量特性、气蚀特性和飞逸特性，指出竖井贯流泵站装置效率高，特别适用于平原水网地区的防洪排涝工程。徐磊等[9]针对南水北调东线一期工程中的邳州泵站，多视角剖析流道表面的流场和垂直于x、y、z3 个方向剖面的流场，并通过水工模型和装置模型试验验证邳州泵站装置水力性能优异。关醒凡等[10]给出了邳州泵站两个不同水泵装置模型在天津中水北方勘测设计研究院试验台的测试结果，得出了竖井贯流泵效率不低于灯泡式贯流泵，抗汽蚀性能好的结论。王秋景[11]数模比较了江苏九圩港泵站初设方案与优化方案在竖井段、出水段和水泵装置的内部流场，优化竖井流道尾部型线。肖玉平等[12]、杨雪林等[13]结合实际工程中的大型竖井贯流泵站，利用三维湍流数值模拟优化了流道型线。刘君等[14]、杨帆等[15]基于三维定常流动数值模拟，研究了前、后置竖井贯流泵装置内部流动的差异，并比较前、后置竖井贯流泵装置的外特性。综上所述，竖井贯流泵站经过十多年的研究，已取得一些成果和经验，但是大都聚焦于流道型线优化，有关水泵与进出水流道水力耦合所诱发的水力特性变异性研究较少。实际工程中出现了小流量时水泵振动明显，带中隔墩的出水流道出流不均衡等问题。为此，本文利用三维湍流数值模拟深入研究竖井贯流泵装置的水力特性，阐释工程现象的内在原因。

1 数值模拟模型

研究选用某实际工程中的典型竖井贯流泵站为数值模拟研究对象。该泵站设计排涝流量为150 m3/s，设计净扬程0.32 m，最大净扬程1.22 m，最小净扬程0 m。4台叶轮直径D=3.9 m的竖井贯流泵，转速n=67 r/min。

泵装置数值模拟模型的物理区域包括进水池、竖井进水流道、水泵段、出水流道、闸室段和出水池，如图1所示。模型水泵采用TJ04-ZL-07水力模型。

图1 水泵装置CFD计算区域

进水池和竖井进水流道、出水流道和出水池均是利用Creo Parameteric 3.0软件三维实体造型、Gambit软件网格剖分，如图2和图3所示。

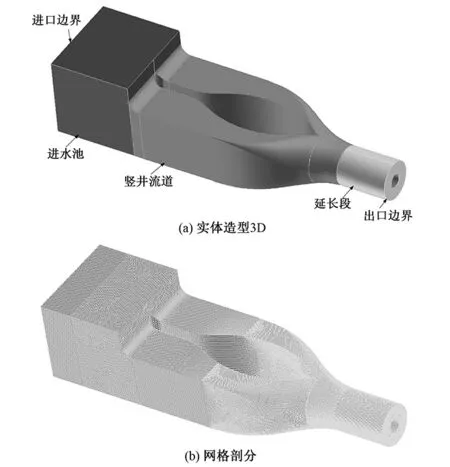
图2 进水池和进水流道三维造型和网格剖分

图3 出水池和出水流道三维造型和网格剖分

水力模型三维造型和网格剖分则是将TJ04-ZL-07的叶轮和导叶的木模图参数化，然后再导入Turbogrid软件中构建。水泵的三维造型和网格剖分见图4。

图4 水力模型的网格剖分

不带水泵(非耦合)的进出水流道的数值模拟模型采用图2、图3模型即可，但水泵装置整体数值模拟模型需去除进、出水流道延长段，再将进水池、竖井进水流道、出水流道、出水池以及水泵段的网格全部导入CFX-Pre16.0中，组装成水泵装置，如图5所示。

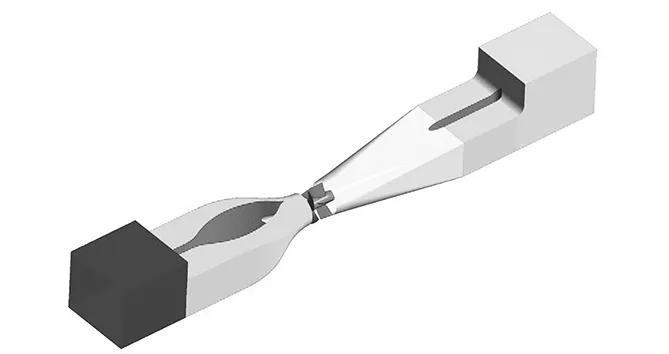
图5 水泵装置数值模拟模型

2 数值模拟方法

2.1 数学模型

假设竖井进水流道内水体为不可压缩牛顿流体，流动为定常流动。张量形式的雷诺时均N-S方程(RANS)和连续方程表达为：

(1)

(2)

其中：

μeff=μ+μt；p*=p+2/3ρk

式中：p为流体密度；ui为雷诺时均速度；μeff为有效黏性系数，等于分子黏性系数μ与Boussinesq涡团黏性系数μt之和；xi(i=1，2，3)代表坐标系坐标轴。

湍流模型采用标准的k-ε模型，则湍动能k和耗散率ε输运方程为：

(3)

(4)

其中：

μt=ρCμk2/ε

式中：μi为涡团黏性系数；Pk是湍动能生成项；Cμ、Cε1，Cε2，σk，σε为经验系数。

2.2 边界条件设置

水泵装置整体数值模拟的进口边界设置在进水池，并设定进口断面的质量流量；出口边界则是设置在出水池，并给定出口静压力(opening)；叶轮与竖井进水流道交界面、叶轮与导叶交界面的连接均设为general connection，参考坐标系为frozen rotor；导叶与出水流道交界面为general connection，参考坐标系静止。计算中，水泵转轮区域设定为旋转区域，转速为67 r/min；叶轮轮毂和叶片相对旋转区域静止，其他区域为静止区域；除叶轮叶片和轮毂外，所有其他固体壁面均为静止无滑移壁面；自由水面设定为对称面。

3 数值模拟方法验证

数值模拟结果的准确性很大程度取决于三维建模、网格剖分、数学模型、边界条件、算法及参数设置等。为了确保竖井贯流水泵装置建模和数值模拟方法的合理性，首先计算Q=15 m3/s时，水泵装置内最小雷诺数的Re=1.13×106，因此水流处于充分湍流区，再根据水泵装置CFD数值计算结果，按照式(5)～ 式(7)计算得到水泵装置的能量特性，并将它与模型试验结果进行了比较，如图4所示。结果表明，两者的流量-扬程曲线、流量-效率曲线规律趋势完全相同，且在水泵装置运行净扬程0～1.22 m范围内，相同净扬程下，流量相对偏差小于3.53%，只是在超过运行净扬程范围小流量区，流量相对偏差会变大。因此，本文的建模和数值模拟方法是合理的。

水泵装置扬程计算采用基于质量流量加权平均的总压力差，即：

(5)

式中：下标1、2分别代表水泵装置进口断面和水泵装置出口断面；其中Ai为各微元的面积；vai为垂直与断面的流速；ρ为水体密度。

水泵装置的轴功率：

(6)

式中：∑M为作用在水泵叶片和轮毂上的力矩之和，N.m；n为水泵转速，r/min。

水泵装置效率表达为：

(7)

式中：Q为水泵流量，m3/s；η为水泵效率。

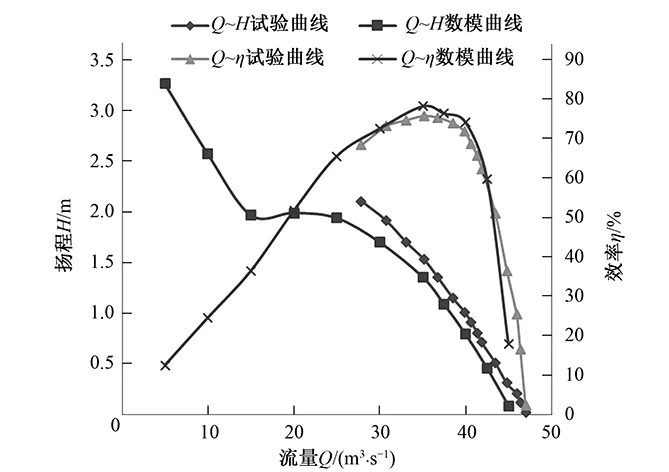
图6 水泵装置能量特性的数模与试验结果

4 水力特性数模结果与分析

4.1 水泵进口断面速度环量

水泵进口断面的涡量和环量大小是反映水泵叶轮旋转对进水流道内流影响的重要指标。

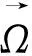
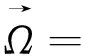
(8)

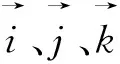
断面速度环量Γ定义为：

(9)

按照式(8)和式(9)计算得到水泵进口断面(即是竖井进水流道出口断面)的速度环量如图7所示。结果表明：大流量时，速度环量很小且几乎不变；小流量的速度环量较大，而速度环量增大与马鞍区具有明显对应关系。可以推断，实际工程中竖井贯流泵装置小流量运行时的振动增强应与此有关。

图7 水泵进口断面速度环量

4.2 进水流道水力损失特性

对竖井进水流道的进、出口断面采用加权平均法计算该断面的总能量，再按下式计算流道水力损失Δh：

(10)

式中：下标1、2分别代表流道进口和出口；Ai为各微元面积；vai为垂直与断面流速。

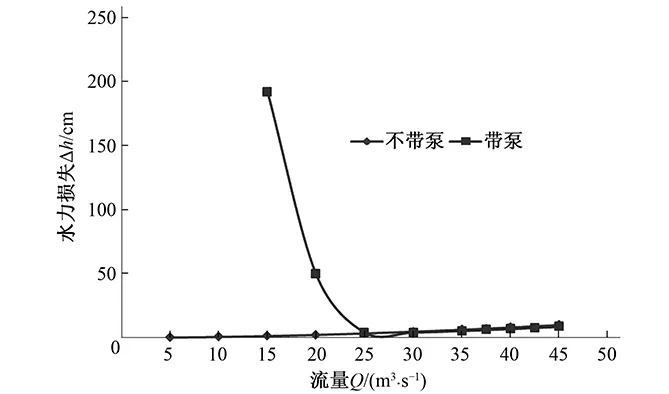
图8 进水流道水力损失曲线

由图8计算结果可知：水泵与进水流道耦合(带水泵)和非耦合(不带水泵)计算得到的竖井进水流道水力损失存在明显差异；耦合时小流量工况，受到水泵转轮的旋转扰动，扰动波向竖井流道内传播，水泵进口断面速度环量急剧增大导致进水流道水力损失也相应急剧增大，致使出现水力损失随流量减小而增大的畸变；大流量时，速度环量较小，带水泵的进水流道水力损失与不带水泵的进水流道水力损失接近，阻力系数为5.1×10-5s/m2。进水流道水力损失规律与水泵进口断面速度环量具有显著关联性。

4.3 水泵进口断面流速分布均匀度Vu和流速加权平均角

(11)

(12)

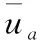
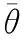
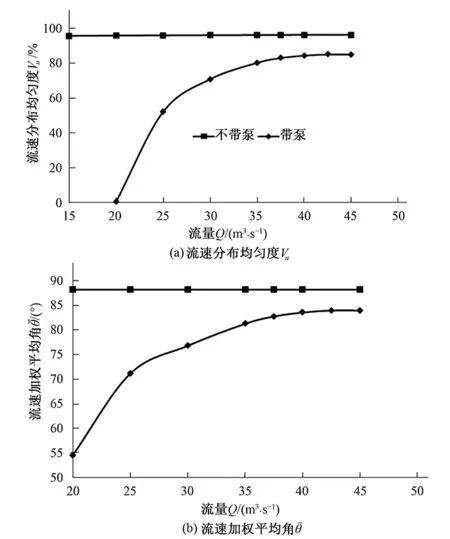
图9 流速分布均匀度Vu和流速加权平均角

4.4 水泵出口断面速度环量

水泵出口断面速度环量会影响出水流道水力特性，为此，根据水泵装置数模结果，仍按照式(9)计算得到水泵出口断面的速度环量，如图10所示。计算结果表明：导叶消减速度环量是不充分的，水泵出口存在6.84～12.21 m2/s的速度环量，且呈现具有极值曲线，大流量时速度环量变小且变化趋缓。

图10 水泵出口断面速度环量

4.5 出水流道水力损失特性

出水流道进口断面与水泵装置出口边界断面的总能量差即是出水流道水力损失。仍采用式(10)计算出水流道的水力损失Δhsc，如图11所示。计算结果表明：非耦合时的出水流道水力损失与流量平方成正比，但耦合时的出水流道水力损失曲线与不带泵的存在差异，它是开口向上的具有极小值的曲线。小流量时，两者差异较大，此系因水泵与出水流道耦合存在速度环量所致；大流量时，差值较小。

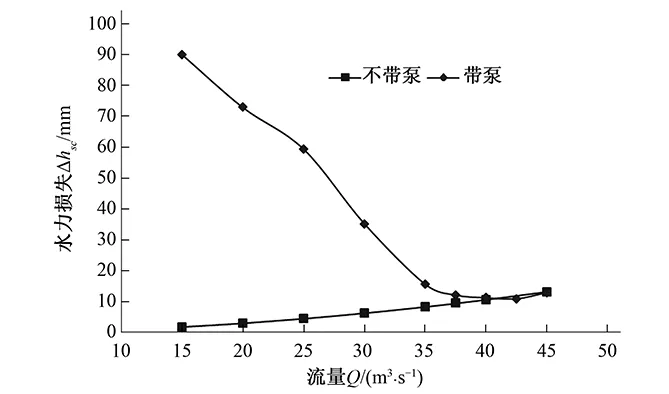
图11 出水流道水力损失曲线

4.6 水泵装置内流线与水泵出口断面涡角

出水流道中流线的扭曲程度可定量地用水泵出口断面的平均涡角表示：

(13)

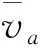
平均涡角小，流线扭曲剧烈，反之则相反。由计算结果图12可知，竖井贯流泵装置在水泵出口断面的平均涡角随流量增大而增大，这表明随流量增加，流线扭曲程度减弱。

图13清晰描述不同工况下水泵与出水流道耦合所诱发的流场变化。从中可看出：小流量工况时，出水流道内出现了强烈的螺旋流动，而随流量增大螺旋强度明显减弱，此与平均涡角的变化规律完全一致。强螺旋流不仅会增大出水流道水力损失，而且造成设置导流墩的出水流道出口两孔流量不均衡，计算表明，在净扬程0～1.22 m范围的两孔流量最大相对差值小于3.2%，大流量时，更均衡。

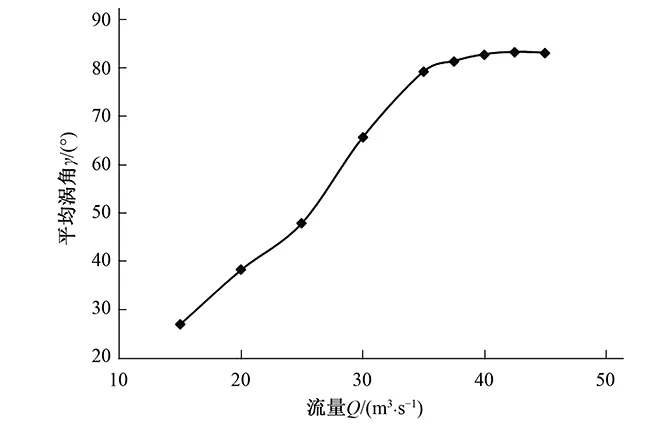
图12 水泵出口断面的平均涡角

图13 水泵装置内部螺旋流动演变

5 结 语

(1)水泵与进出水流道耦合作用导致进出水流道水力损失规律与不带水泵非耦合时的进出水流道水力损失存在较大差异；因此，优化竖井贯流泵站的进出流道应带上水泵段。

(2)在小流量工况，水泵旋转所诱发的扰动波会向进水流道传播，导致水泵入口的速度均匀度和流速加权平均角明显减小；大流量时，扰动明显减弱，但带泵的速度均匀度和流速加权平均角较不带泵稍差些。

(3)水泵导叶消除水泵出口速度环量是不充分的，水泵叶片出口边的螺旋运动会延伸至出水流道内。小流量工况， 流道内螺旋流动强度较大，大流量工况相对较弱。

(4)有关轴流泵不稳定马鞍区产生原因有诸多解释，但从本文数值结果看，小流量时水泵旋转诱导进水流道水流旋转，获得能量的水流并再次进入水泵，可能是导致马鞍区原因之一。