基桩正常使用极限状态失效概率区间估计方法
桑 意 平
(1. 武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072;2. 武汉大学 水工岩石力学教育部重点实验室,武汉 430072)
0 引 言
基桩是岩土工程中常见的岩土结构物。在基桩正常使用极限状态失效概率估计中,表征荷载-位移关系的双曲线参数通常被视为关键的随机变量[1-7]。此外,现有研究[5-7]表明基桩荷载-位移双曲线参数具有明显的负相关性,且这种负相关性对基桩失效概率的估计具有显著的影响,忽略双曲线参数的负相关性将严重高估基桩的失效概率。为了更加准确地估计基桩失效概率,实际工程应该充分考虑双曲线参数的负相关性,建立双曲线参数的二维分布模型。近年来,Copula方法[8]为基桩荷载-位移双曲线参数二维分布模型的建立提供了一条简单而有效的途径[5-7]。Copula方法相比其他方法的优势是,它将二维分布模型的构造简化为边缘分布函数的估计与Copula函数的选择问题,且边缘分布函数估计与Copula函数选择分开独立进行[5-7]。
试验数据是Copula方法构造二维分布模型的基础。当试验数据的样本数目无穷大时,基于试验数据建立的二维分布模型是精确的。然而,受技术经济条件的限制,实际工程中试验数据非常有限,基于有限试验数据建立的二维分布模型不可避免地存在较大的统计不确定性,这是因为基于有限试验数据估计的统计量如样本均值、标准差、相关系数和AIC值具有明显的变异性[9,10]。传统的基桩失效概率估计方法几乎无一例外地忽略了双曲线参数的统计不确定性,这些方法只能得到基桩失效概率的点估计。该点估计仅考虑了双曲线参数本身固有的变异性,而没有考虑因试验数据有限引起的统计不确定性。由于统计不确定性的存在,失效概率的点估计可能无法真实反映基桩的安全度。根据统计学理论,当考虑双曲线参数的统计不确定性时,基桩失效概率本质上是一个概率分布,此时将基桩失效概率表示为具有一定置信度水平的置信区间即失效概率的区间估计是一种更加合理的方法[11-13]。
实现基桩失效概率区间估计的关键一步是表征双曲线参数二维分布模型的统计不确定性。该统计不确定性可以通过直接模拟双曲线参数试验数据的统计量如样本均值、标准差、相关系数和AIC值的变异性来表征。然而,常规方法模拟统计量变异性需要已知大量与试验数据相同样本数目的样本,这在工程上是不可能实现的。幸运的是,作为重抽样方法的Bootstrap方法[14]为统计量变异性的直接模拟提供了一种有效的工具。Bootstrap方法通过对原始试验数据进行有放回地随机抽样获得大量的与原始试验数据相同样本数目的Bootstrap子样本,基于Bootstrap子样本即可计算统计量的估计值并获得统计量的变异性。Bootstrap方法模拟统计量变异性只需已知原始试验数据,无需对统计量的实际分布作任何假设和增加新的数据观测。Bootstrap方法的上述优点使得它在岩土工程领域岩土体参数统计量变异性模拟方面获得了广泛的应用[10-13]。
本文目的在于提出基桩正常使用极限状态失效概率区间估计方法,推动基桩失效概率估计从传统的点估计向区间估计转变。为此,首先介绍了基桩标准化荷载-位移双曲线参数的定义,并给出了钻孔现浇灌注桩(ACIP)双曲线参数的现场试验数据。其次,基于试验数据采用Copula方法构造了双曲线参数的二维分布模型,并应用Bootstrap方法表征了双曲线参数二维分布模型的统计不确定性。最后,给出了考虑双曲线参数二维分布模型统计不确定性的基桩失效概率区间估计方法,并比较了基桩失效概率点估计和区间估计结果的优缺点。
1 基桩标准化荷载-位移双曲线模型
1.1 双曲线参数的定义
基桩的荷载-位移关系是基桩设计的基础。为了得到基桩的荷载-位移关系,首先需要开展荷载试验获取荷载-位移数据,然后采用一定的模型如双曲线模型、幂函数模型、指数函数模型、GM(1, 1)模型等拟合荷载-位移数据,从而得出基桩的荷载-位移关系曲线。由于参数较少且物理意义明确,双曲线模型在拟合基桩的荷载-位移关系曲线中应用最为广泛。为了进一步减小实测基桩荷载-位移双曲线的离散性,有学者[4-5]提出采用基桩的实测极限承载力对基桩荷载-位移双曲线模型进行标准化,该标准化的基桩荷载-位移双曲线模型如下式所示:
(1)
式中:Q为基桩轴向荷载;QSTC为基桩的实测极限承载力;y为桩端位移;a和b是双曲线模型中两个参数,它们均具有明确的物理意义(见图1),其中a为双曲线初始斜率的倒数,而b为双曲线极限值的倒数。可见,基桩标准化荷载-位移双曲线模型由双曲线参数a和b唯一确定。

图1 双曲线参数的定义Fig.1 Definition of hyperbolic curve-fitting parameters
1.2 双曲线参数现场试验数据
如前所述,双曲线参数a和b是基桩正常使用极限状态失效概率估计的关键变量。为此,以文献[6]中钻孔现浇灌注桩(ACIP)双曲线参数现场试验数据(样本数目N=40,属于非常有限的试验数据)为例建立a和b的二维分布模型,并估计基桩的正常使用极限状态失效概率。图2给出了双曲线参数试验数据的散点图及其生成的40条基桩荷载-位移双曲线。由于场地变异性和基桩制造缺陷的存在,同一场地的同类型基桩得到的荷载-位移关系曲线并不相同,而是表现出明显的离散性,与之对应的荷载-位移双曲线参数a和b展现出显著的变异性。此外,a和b还具有明显的负相关性,由试验数据计算知:a和b的Kendall秩相关系数τ为-0.548。下面采用Copula方法建立a和b的二维分布模型以表征a和b的变异性和负相关性。

图2 双曲线参数试验数据及基桩标准化荷载-位移双曲线Fig.2 Test data for a and b and the resulting normalized hyperbolic load-displacement curves for single piles
2 基于Copula方法的双曲线参数二维分布模型构造
2.1 Copula方法
本文采用Copula方法构造双曲线参数a和b的二维分布模型。根据Sklar定理[8],a和b的联合分布函数F(a,b) 和联合概率密度函数f(a,b)可以分别表示为:
F(a,b)=C[F1(a),F2(b);θ]=C(u1,u2;θ)
(2)
f(a,b)=f1(a)f2(b)D[F1(a),F2(b);θ]=
f1(a)f2(b)D(u1,u2;θ)
(3)
式中:C(u1,u2;θ)为二维Copula函数;D(u1,u2;θ)为二维Copula函数的密度函数;θ为Copula函数的相关参数;u1=F1(a)和u2=F2(b)分别为a和b的边缘分布函数;f1(a)和f2(b)分别为a和b的概率密度函数。因此,若已知a和b的边缘分布函数和Copula函数,利用式(2)和式(3)就可以构造出a和b的联合分布函数和联合概率密度函数。
2.2 双曲线参数二维分布模型
Copula方法构造双曲线参数a和b的二维分布模型包括以下独立的两步:①确定a和b的边缘分布函数;②选择最优的Copula函数表征a和b的相关结构。基于图2所示的试验数据,下面采用Copula方法构造a和b的二维分布模型。
首先确定a和b的边缘分布函数。为此,选取岩土工程中常用的正态分布、对数正态分布、极值I型分布和威布尔分布作为备选边缘分布函数拟合a和b的边缘分布。为了避免出现负值,正态分布和极值I型分布在0处进行左截尾。上述4种边缘分布函数的分布参数可以利用a和b的均值和标准差求出(a的均值和标准差分别为5.15和3.07 mm;b的均值和标准差分别为0.62和0.16)。
在确定了备选边缘分布函数的分布参数之后,下一步就是采用AIC准则[15]识别出拟合试验数据最优的边缘分布函数。一般来说,具有最小AIC值的边缘分布函数被认为是拟合试验数据最优的边缘分布函数。对于参数a来说,基于试验数据计算的正态、对数正态、极值I型和威布尔分布的AIC值分别为202.47、196.03、194.71和196.53,最优的边缘分布是极值I型分布;对于参数b而言,4种分布的AIC值分别为-29.12、-30.32、-28.26和-27.53,最优的边缘分布是对数正态分布。
其次选择最优的Copula函数表征a和b的相关结构。众所周知,数学上存在多种二维Copula函数可以用来拟合随机变量的相关结构,如Gaussian、Plackett、Frank、Clayton、Gumbel、FGM、AMH Copula等。鉴于a和b具有明显的负相关性,选取岩土工程中常用的Gaussian、Plackett、Frank和No.16 Copula函数[8]作为备选Copula函数拟合a和b的相关结构。上述4种Copula函数都能表征a和b的负相关性,且相关系数绝对值都能达到1,非常适合表征a和b的相关结构[8]。这些Copula函数的相关参数θ可以利用a和b的Kendall秩相关系数τ求出(Kendall秩相关系数τ为-0.548)。
在确定了备选Copula函数的相关参数θ之后,下一步就是采用AIC准则[15]识别出拟合试验数据最优的Copula函数。同理,具有最小AIC值的Copula函数被认为是拟合试验数据相关结构最优的Copula函数。为此,计算了Gaussian、Plackett、Frank和No.16 Copula函数的AIC值,它们分别为-27.01、-31.37、-27.52和-28.25,可见Plackett Copula函数是拟合钻孔现浇灌注桩(ACIP)的双曲线参数相关结构最优的Copula函数。
3 基于Bootstrap方法的双曲线参数统计不确定性表征
3.1 Bootstrap方法
如前所述,基于有限试验数据估计的统计量如样本均值、标准差、相关系数和AIC值具有较大的变异性,这种变异性导致基于有限试验数据建立的二维分布模型存在明显的统计不确定性。为了表征a和b的二维分布模型的统计不确定性,本文采用Bootstrap方法模拟双曲线参数试验数据的统计量变异性。Bootstrap方法由Efron于1979年提出,它的基本原理是:通过对原始试验数据进行有放回地随机抽样获得大量与原始试验数据相同样本数目的Bootstrap子样本,然后基于Bootstrap子样本计算统计量的估计值,最终获得统计量的变异系数及其概率分布。Bootstrap方法只需已知原始试验数据,无需对统计量的实际分布作任何假设以及增加新的数据观测。尽管简单,但是该方法的理论依据及其良好的收敛性早已被统计学家所证明[14]。
令双曲线参数的试验数据为X={(ai,bi),i= 1, 2,…,N},从中有放回地随机抽样N次,每次抽取双曲线参数的一次观测,从而得到一个与X相同样本数目的Bootstrap子样本Bj={B1,j,B2,j, …,BN,j},该抽样过程如图3所示。由于是有放回地随机抽样,因此在Bj中双曲线参数的某次观测(ai,bi)可能出现一次、多次或零次。重复上述步骤Ns次,即可获得Ns个Bootstrap子样本。一般来说,为了达到良好的收敛效果,Bootstrap子样本数目Ns通常取值较大。参考前人的研究结果[10-13],本文采用Ns=104模拟统计量如样本均值、标准差、相关系数和AIC值的变异性。Ns个Bootstrap子样本可以得到Ns组样本均值、标准差、相关系数和AIC值。根据这些数值即可获得样本均值、标准差、相关系数和AIC值的概率分布和变异系数。
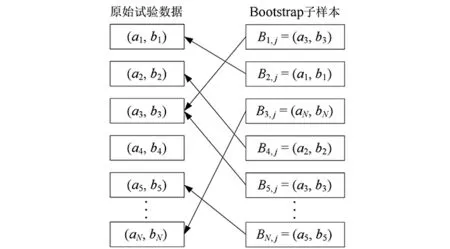
图3 Bootstrap方法抽样示意图Fig.3 The generation of one bootstrap sample
3.2 双曲线参数统计不确定性
由于Copula方法构造的二维分布模型由边缘分布函数和Copula函数组成,因此研究双曲线参数二维分布模型的统计不确定性可以转化为研究边缘分布函数和Copula函数的统计不确定性。
首先研究边缘分布函数的统计不确定性。图4给出了Bootstrap方法模拟的a和b样本均值和样本标准差的概率密度函数。可以看出,基于有限数据估计的样本均值和标准差具有较大的变异性,如a的样本均值和标准差的变异系数分别为0.09和0.17,b的样本均值和标准差的变异系数分别为0.04和0.12,可见高阶矩的样本标准差比低阶矩的样本均值变异性更大,表明样本标准差比样本均值更加难以准确估计。样本均值和标准差的变异性将导致a和b的边缘分布函数的分布参数具有统计不确定性,这是因为边缘分布函数的分布参数是根据样本均值和标准差确定的。

图4 样本均值和标准差的概率密度函数Fig.4 Probability density functions of sample mean and standard deviation for a and b
图5给出了Bootstrap方法模拟的4种备选边缘分布函数AIC值的概率密度函数。可以看出,基于有限数据估计的AIC值也具有较大的变异性。对于参数a来说,正态、对数正态、极值I型和威布尔分布的AIC值变异系数分别为0.06、0.06、0.06和0.06;对于参数b而言,4种分布AIC值变异系数分别为0.30、0.27、0.29和0.31。4种备选边缘分布函数AIC值的变异性将导致a和b的边缘分布函数的分布类型具有统计不确定性,这是因为边缘分布函数的分布类型是根据AIC值识别的。此外,4种备选边缘分布函数AIC值的概率密度函数重叠区域较大,这进一步说明4种备选边缘分布都有可能被识别为最优边缘分布函数。下面分析a和b的边缘分布函数的分布类型不确定性。

图5 4种备选边缘分布函数AIC值的概率密度函数Fig.5 Probability density functions of AIC scores for the four candidate marginal distributions
基于每个Bootstrap子样本计算的4种备选边缘分布函数的AIC值即可识别出该子样本的最优边缘分布函数,Ns个Bootstrap子样本就可以得到Ns个最优边缘分布函数。为了表征分布类型不确定性,统计4种备选边缘分布函数被识别为最优边缘分布的次数。对于参数a来说,Ns=104个Bootstrap子样本中正态、对数正态、极值I型和威布尔分布被识别为最优边缘分布的次数分别为94、3 435、3 958和2 513;对于参数b而言,4种分布被识别为最优边缘分布的次数分别为2 334、5 282、1 048和1 336。可见,在考虑AIC值的变异性时没有一种备选边缘分布函数能够100%被识别为最优边缘分布。上述结果表明:基于有限试验数据确定的a和b的边缘分布函数存在较大的统计不确定性,包括分布参数不确定性和分布类型不确定性。
其次研究Copula函数的统计不确定性。图6给出了Kendall秩相关系数的概率密度函数。可以看出,基于有限数据估计的Kendall秩相关系数也具有较大的变异性,其变异系数为0.17。Kendall秩相关系数的变异性将导致a和b的Copula函数的相关参数具有统计不确定性,这是因为Copula函数的相关参数是根据Kendall秩相关系数确定的。

图6 Kendall秩相关系数的概率密度函数Fig.6 Probability density function of Kendall rank correlation coefficient between a and b
图7给出了4种备选Copula函数AIC值概率密度函数。可以看出,基于有限数据估计的Copula函数的AIC值也具有较大的变异性,Gaussian、Plackett、Frank和No.16 Copula函数的AIC值变异系数分别为0.39、0.39、0.40和0.46。4种备选Copula函数AIC值的变异性将导致a和b的Copula函数类型具有统计不确定性,这是因为Copula函数类型是根据AIC值识别的。此外,4种备选Copula函数AIC值的概率密度函数重叠区域较大,这说明4种备选Copula都有可能被识别为最优Copula函数。下面分析a和b的Copula函数类型不确定性。

图7 4种备选Copula函数AIC值的概率密度函数Fig.7 Probability density functions of AIC scores for the four candidate copula functions
基于每个Bootstrap子样本计算的4种备选Copula函数的AIC值即可识别出该子样本的最优Copula函数,Ns个Bootstrap子样本可以得到Ns个最优Copula函数。为了表征Copula类型不确定性,统计4种备选Copula函数被识别为最优Copula的次数,可以得出Ns=104个Bootstrap子样本中Gaussian、Plackett、Frank和No.16 Copula函数被识别为最优Copula的次数分别为2 251、5 233、9 67和1 549。可见,在考虑AIC值的变异性时没有一种备选Copula函数能够100%被识别为最优Copula。上述结果表明:基于有限试验数据确定的a和b的Copula函数存在较大的统计不确定性,包括Copula函数的相关参数不确定性和类型不确定性。
4 基桩正常使用极限状态失效概率估计
4.1 失效概率计算方法
上面应用Bootstrap方法表征了a和b二维分布模型的统计不确定性,下面进一步给出考虑a和b二维分布模型统计不确定性的基桩正常使用极限状态失效概率区间估计方法。首先给出基桩正常使用极限状态失效概率计算方法。
对于基桩正常使用极限状态来说,当基桩实际位移大于允许位移时认为基桩失效,基桩失效概率计算的功能函数为[5]:
g=ya-y(Q)
(4)
式中:ya为基桩允许位移;y(Q)为外荷载Q时基桩的位移。如果将ya对应的荷载表示为Qa,可得基桩正常使用极限状态失效概率计算另一种表述方式,即当基桩实际荷载Q大于允许荷载Qa时认为基桩失效,基桩失效概率计算的功能函数为[5]:
g=Qa(ya)-Q
(5)
由于荷载数据比位移数据更加容易获得,这里采用式(5)计算基桩正常使用极限状态失效概率,相应的失效概率pf为:
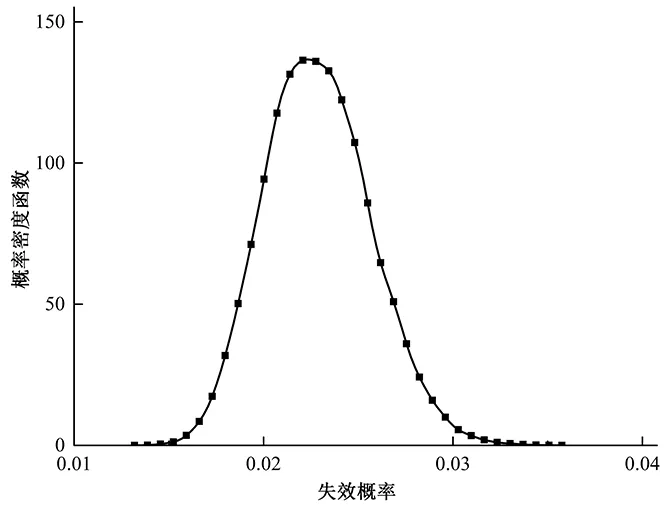
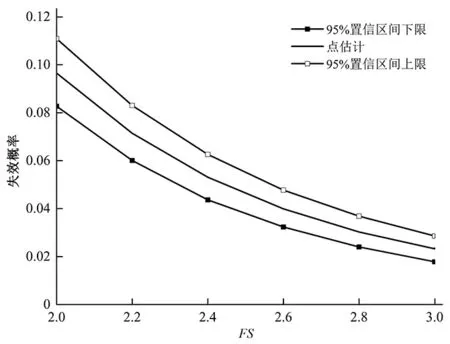
pf=P(Qa(ya) (6) 将式(1)代入可得: (7) 从式(7)可以看出,计算基桩正常使用极限状态的失效概率涉及5个随机变量:a、b、ya、Q和QSTC。为此,将式(7)进一步表示为: (8) 在给出基桩失效概率区间估计之前,首先给出传统方法计算的基桩失效概率点估计。如前所述,基桩失效概率点估计是忽略a和b的二维分布模型统计不确定性或直接采用基于试验数据建立的二维分布模型的结果。基于双曲线参数试验数据,本文第2节建立了a和b的二维分布模型,即a和b的最优边缘分布函数分别为极值I型分布和对数正态分布,a和b的最优Copula函数为Plackett Copula函数。上述最优边缘分布函数的分布参数和最优Copula函数的相关参数采用基于试验数据计算的样本均值、标准差和Kendall秩相关系数确定。下面给出基桩失效概率点估计结果。 基于本文第2节建立的a和b的二维分布模型,利用蒙特卡洛模拟方法即可计算出基桩失效概率的点估计。表1第2列给出了FS=3.0、2.5和2.0时基桩失效概率的点估计结果。可以看出,基桩失效概率随FS的减小而增大。基桩失效概率位于10-2量级,可见本文设定的蒙特卡洛模拟次数完全满足精度要求。此外,忽略a和b的二维分布模型统计不确定性,传统方法只能得到基桩失效概率的点估计。由本文第3节可知,a和b的二维分布模型具有较大的统计不确定性。因此,基桩失效概率的点估计可能无法真实反映基桩的安全度。针对上述问题,本文提出了基桩失效概率区间估计方法。该方法通过考虑a和b的二维分布模型统计不确定性,得出基桩失效概率的概率密度函数,并将失效概率表示为具有一定置信度水平的置信区间。下面给出该方法的具体实现步骤。 表1 基桩失效概率点估计和区间估计Tab.1 Point and interval estimates of probability offailure of single piles 本节进一步给出基桩失效概率区间估计。实现基桩失效概率区间估计的关键是成功模拟失效概率的概率分布。首先,基于每个Bootstrap子样本识别的最优边缘分布函数和最优Copula函数建立a和b的二维分布模型。其次,基于每个Bootstrap子样本的二维分布模型利用蒙特卡洛模拟方法计算出该子样本的失效概率,Ns个Bootstrap子样本就可以得到Ns个失效概率。最后,基于Ns个失效概率采用常规统计方法即可获得失效概率的均值、标准差、变异系数和概率分布。 图8以FS=3.0为例给出了基桩失效概率的概率密度函数。由于a和b的二维分布模型统计不确定性的存在,基桩失效概率具有明显的变异性,如FS=3.0时基桩失效概率的变异系数达到了0.121。为了表征基桩失效概率的变异性,本文将基桩失效概率表示为具有一定置信度水平的置信区间。为了简单起见,将基桩失效概率的97.5%和2.5%分位数分别作为基桩失效概率的95%置信区间的上下限。表1给出了基桩失效概率区间估计结果,包括基桩失效概率均值、标准差、变异系数和95%置信区间。与传统方法计算的基桩失效概率点估计相比,由于考虑了a和b的二维分布模型统计不确定性,基桩失效概率区间估计能够更加合理地表征基桩的真实可靠度水平。 图8 基桩失效概率的概率密度函数Fig.8 Probability density function of probability of failure of single piles 为了研究FS对基桩失效概率置信区间的影响,图9给出了基桩失效概率的95%置信区间随FS的变化曲线。为了比较,图中还给出了基桩失效概率的点估计。可以看出,基桩失效概率95%置信区间的上下限随FS的降低而增加,基桩失效概率置信区间的变化范围亦随FS的降低而增大。基于传统方法计算的基桩失效概率的点估计只能反映基桩的平均可靠度水平,而不能给出基桩失效概率的变异系数及其上下限。与其相反,基桩失效概率区间估计方法能够有效得到基桩失效概率的概率分布及其置信区间。这种置信区间不仅能够更加准确地表征基桩的可靠度,而且便于工程设计人员进行基桩的加固设计。这是因为工程设计人员能够方便地看到基桩失效概率的上下限随FS的变化关系。 图9 基桩失效概率随FS的变化曲线Fig.9 Variation of probability of failure of single piles with factor of safety (1)基于有限双曲线参数试验数据估计的样本均值、标准差、Kendall秩相关系数和AIC值具有较大的变异性,这种变异性进一步导致双曲线参数的二维分布模型存在明显的统计不确定性。 (2)Bootstrap方法通过模拟双曲线参数统计量的变异性,有效地表征了双曲线参数二维分布模型的统计不确定性。该方法只需已知双曲线参数试验数据,为有限数据条件下统计量变异性模拟和统计不确定性表征提供了一条有效的途径。 (3)双曲线参数二维分布模型的统计不确定性对基桩失效概率的估计具有重要的影响。有限数据条件下基桩失效概率具有显著的变异性。为了减小基桩失效概率的变异性,建议增加双曲线参数试验数据的样本数目。 (4)通过考虑双曲线参数二维分布模型的统计不确定性,基桩失效概率可以表示为具有一定置信水平的置信区间,而不是传统方法的点估计。基桩失效概率的区间估计相比点估计能更加合理地表征基桩的真实可靠度水平。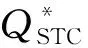
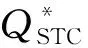
4.2 失效概率点估计
4.3 失效概率区间估计
5 结 语

