基于GM(1,N)模型的临漳县地下水矿化度研究

张紫悦，杜富慧，李明然，李新德，王 渊

(1.河北工程大学水利水电学院，河北 邯郸 056000；2.河北省保定水文水资源勘测局，河北 保定 071000)

0 引 言

我国属于水资源严重短缺的国家之一，近年来，随着经济的迅速发展，导致国内众多地区为了满足各用水部门的需水量，开始大量开采地下水资源，引起了众多的水资源问题[1]。其中河北省邯郸市属于极度缺水地区，由于近年来工农争水矛盾日益加剧，导致农业用水大量超采地下水，地下水常年超采已造成市域内超采区面积达64%[2]。作为本文研究区的临漳县，属于邯郸市严重超采地下水的区域之一，尤其是近年来，随着临漳县人口的增长与经济发展，为满足用水需求大量开采地下水，造成区域地下水位持续下降，引发了地面沉降、水质恶化等环境地质问题，同时，对当地地下水矿化度的变化也产生了影响，威胁到了临漳县的居民用水安全和农作物的生长，引起了人们的普遍关注[3]。

本文将根据邯郸市临漳县2010-2015年地下水矿化度的实测资料，运用灰色方法中的GM(1,N)模型预测其地下水矿化度变化情况。利用GM(1,N)模型原理简单、所需样本系列短且预测精度高的特点[4]，对临漳县2010-2015年的实测资料进行模拟，并将模拟结果与GM(1,1)模型和BP神经网络模型的模拟结果进行比较，确定出误差最小的模型，将该模型的预测结果作为本研究的最终成果。该研究旨在为邯郸市临漳县未来几年的地下水管理和水盐调控等工作提供参考依据。

1 区域概况及数据收集

1.1 研究区概况

临漳县位于河北省邯郸市最南端，地处东经114°19′～114°16′，北纬36°07′～36°24′之间，具体位置如图1所示。属暖温带半湿润半干旱大陆性季风气候区，临漳县属太行山山前冲积和洪积平原，由于漳河在历史上几经摆动，致使河道遍布全县，境内地势起伏，微地貌复杂多变，而且其位于华北平原的干旱区，年降水量偏少，区域水资源紧缺[5]。临漳县属邯郸市农业用水大县之一，由于农业用水长期大量超采地下水，造成了众多水文地质问题，其中引起的地下水矿化度的变化，对当地居民生活用水以及作物生长用水均产生了影响。

图1 临漳县地理位置图Fig.1 Geographical location map of Linzhang county

1.2 基础数据收集

本文以临漳县为研究区域，选择区域内的3口监测井：陈村监测井、香菜营监测井和洛村监测井，监测井具体位置见图1。由于影响矿化度的因子有很多，本文主要考虑的影响因子有井水位，降雨量和开采量，忽略其他的因子。三口井的矿化度和水位数据监测频次均为5 d一次，为了更好地反映不同年份总的变化情况，矿化度和水位均取各年的平均值，降雨量和开采量为临漳县总的年降雨和开采量。则各项监测指标2010-2015年的具体监测数据如表1所示。

表1 监测井各项监测指标值汇总表Tab.1 Summary of monitoring index values for monitoring wells

2 基于地下水矿化度的GM(1,N)模型的建立

GM(1,N)模型是应用于各变量动态关联分析的预测模型，它可以为高阶系统建模提供基础。因此，GM(1,N)反映的虽然是变量的变化规律，但是这个变量的变化都依赖于其他变量的值[6]。在本文中，在利用GM(1,N)模型建立研究区地下水的矿化度模拟模型时，主要依赖于监测井水位、抽水量及区域降雨量等变量的值。基于地下水矿化度的GM(1,N)灰色模型建立可具体分为以下几步：

第一步：确定主导系统的因素和关联系统的因素，围绕研究目的，定性分析系统的特征,也可以结合着关联因素进行定量分析。只有把前提把握准，才能充分认识问题的性质，进而为预测建模的成功打好基础[7]。本文的主导因素为监测井水位、抽水量及区域降雨量等变量，关联因素为监测井的矿化度。

第二步：建立GM(1,N)模型群。一般在预测时，为了调节和输入可控因素，也应建立GM(1,N)模型。该模型可反映一个关联因素对其中某个因素变化率的影响，即与增量的动态关系。则灰色模型的白化微分方程为:

(1)

式中：x1为监测井的矿化度；x2为监测井水位；x3为监测井水位抽水量；x4为区域降雨量。

第三步：是根据GM(1,N)模型建立系统状态方程矩阵，计算系数矩阵B及常数矩阵Y。

(2)

(3)

第四步：计算参数的系列值。

(4)

(5)

第五步：使用已求出的值计算出模拟及预测值。

第六步：计算模拟值与实测值的相对误差及方差比，分析模拟结果的可靠性。

3 结果与分析

3.1 GM(1，N)模型运行结果

将表1的监测数据输入到已经建立好的MATLAB软件中的GM(1,N)模型中，便可以运行得到临漳县地下水中矿化度的模拟及预测值，拟合区间为2010-2015年，预测得到2016-2020年浅层地下水矿化度预测值。同时绘制出地下水水位实测值与模拟、预测值的拟合曲线图。模拟与预测结果见表2。拟合曲线图见图2～4。

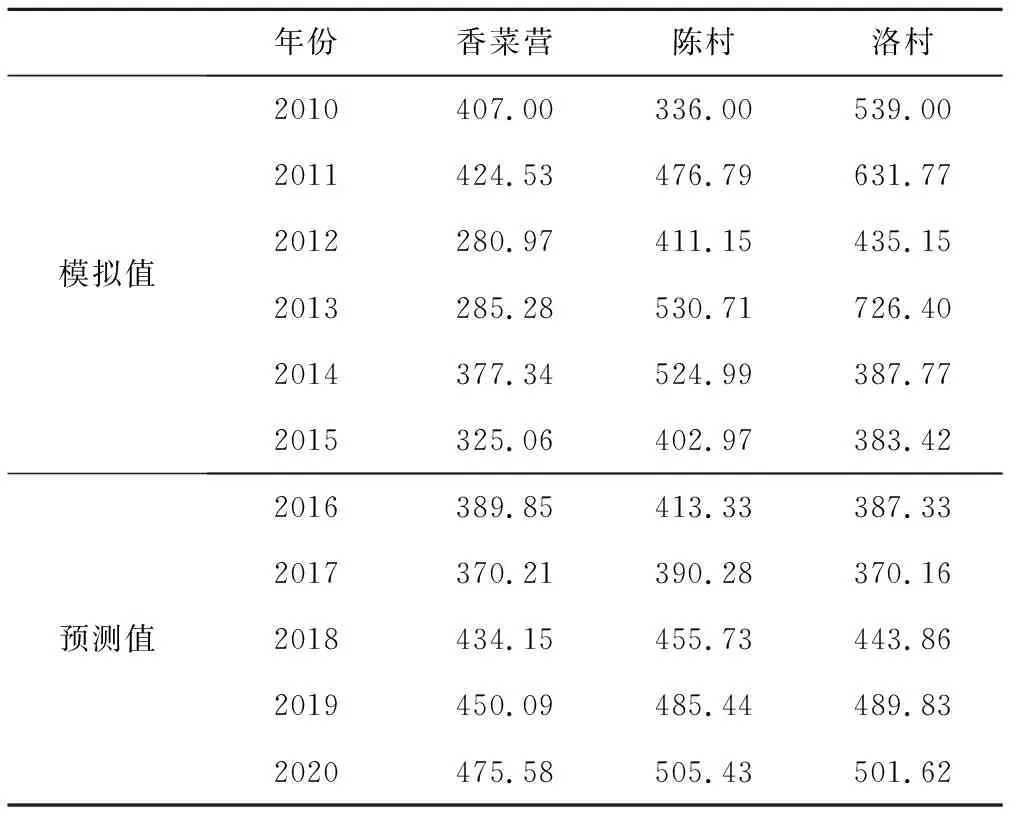
表2 GM(1，N)模型模拟与预测成果表 mg/L

图2 香菜营监测井拟合曲线图Fig.2 Monitoring well fitting curve of Xiangcaiying

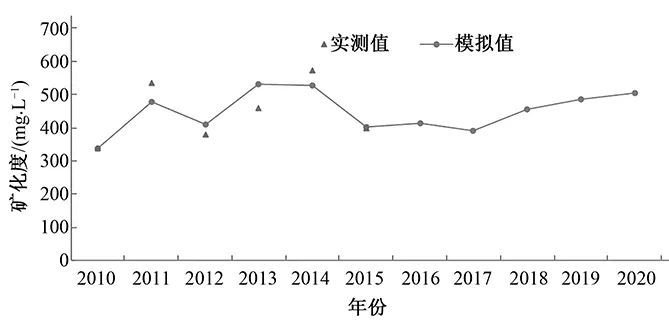
图3 陈村监测井拟合曲线图Fig.3 Monitoring well fitting curve of Chencun

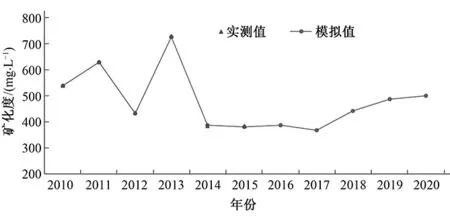
图4 洛村监测井拟合曲线图Fig.4 Monitoring well fitting curve of Luocun

3.2 拟合精度的比较

为了进一步验证GM(1,N)模型预测地下水成果的准确性，同时运用GM(1,1)模型和BP神经网络模型对邯郸市临漳县地下水矿化度进行了模拟，并对三个模型的运行结果进行了对比分析[8]，具体分析如下。

(1)GM(1,1)模型作为灰色预测模型中应用最多，也是最基本的灰色GM(1,1)模型，其原理是根据少量的已知信息，累加生成杂乱无章的原始数据，然后把新生成的数列建立一阶线性微分时间序列模型处理灰色信息，用来研究事物内部的特征及规律[9]。

(2)BP神经网络模型。BP神经网络是多层神经网络和非线性转换函数的结合，它包括输入层、隐含层(中间层)、输出层。其运行过程的实质是权值不断调整的过程，也就是网络的学习训练的过程。最终的结果一直进行到预先设定的学习次数或可接受的网络输出误差为止[10]。

将上述两个模型分别运用到临漳县地下水矿化度模拟中，并将模拟结果与GM(1,N)结果进行比较，分别计算三口监测井在不同模型下的模拟值与实测值的相对误差，详细结果见表3。

由计算结果可知，香菜营监测井在BP神经网络下的模拟值与实测值的平均误差为-1.78%，在GM(1,1)模型下的平均误差为2.09%，在GM(1,N)模型下的平均误差为-0.16%，由结果对比分析可知，香菜营监测井的GM(1,N)模型平均误差最接近0，精度最高；陈村监测井在BP神经网络下的模拟值与实测值的平均误差为5.15%，在GM(1,1)模型下的平均误差为2.07%，在GM(1,N)模型下的平均误差为1.06%，由结果对比分析可知，陈村监测井的GM(1,N)模型平均误差最接近0，精度最高；洛村监测井在BP神经网络下的模拟值与实测值的平均误差为-0.98%，在GM(1,1)模型下的平均误差为4.05%，在GM(1,N)模型下的平均误差为0.04%，由结果对比分析可知，洛村监测井的GM(1,N)模型平均误差最接近0，精度最高。

由各模型的相对误差的初步比较可知，GM(1,N)模型对三口监测井的模拟精度均优于BP神经网络和GM(1,1)模型的模拟精度。为了进一步比较三种方法的模拟精度，分别计算了三种方法的均方根误差，结果见表4。

由均方根误差对比分析可知，GM(1,N)模型下的三口监测井的均方根误差分别为7.62、44.54、2.08，均小于BP神经网络和GM(1,1)模型的均方根误差。主要原因是BP神经网络适合对长系列数据进行预测，而对短系列数据预测精度不高；GM(1,1)模型只考虑了单因素的变化情况对结果的影响。而GM(1,N)模型对短期系列预测精度高且兼顾了多种因素对结果的影响。故结果表明GM(1,N)模型对临漳县地下水矿化度的模拟精度最高。

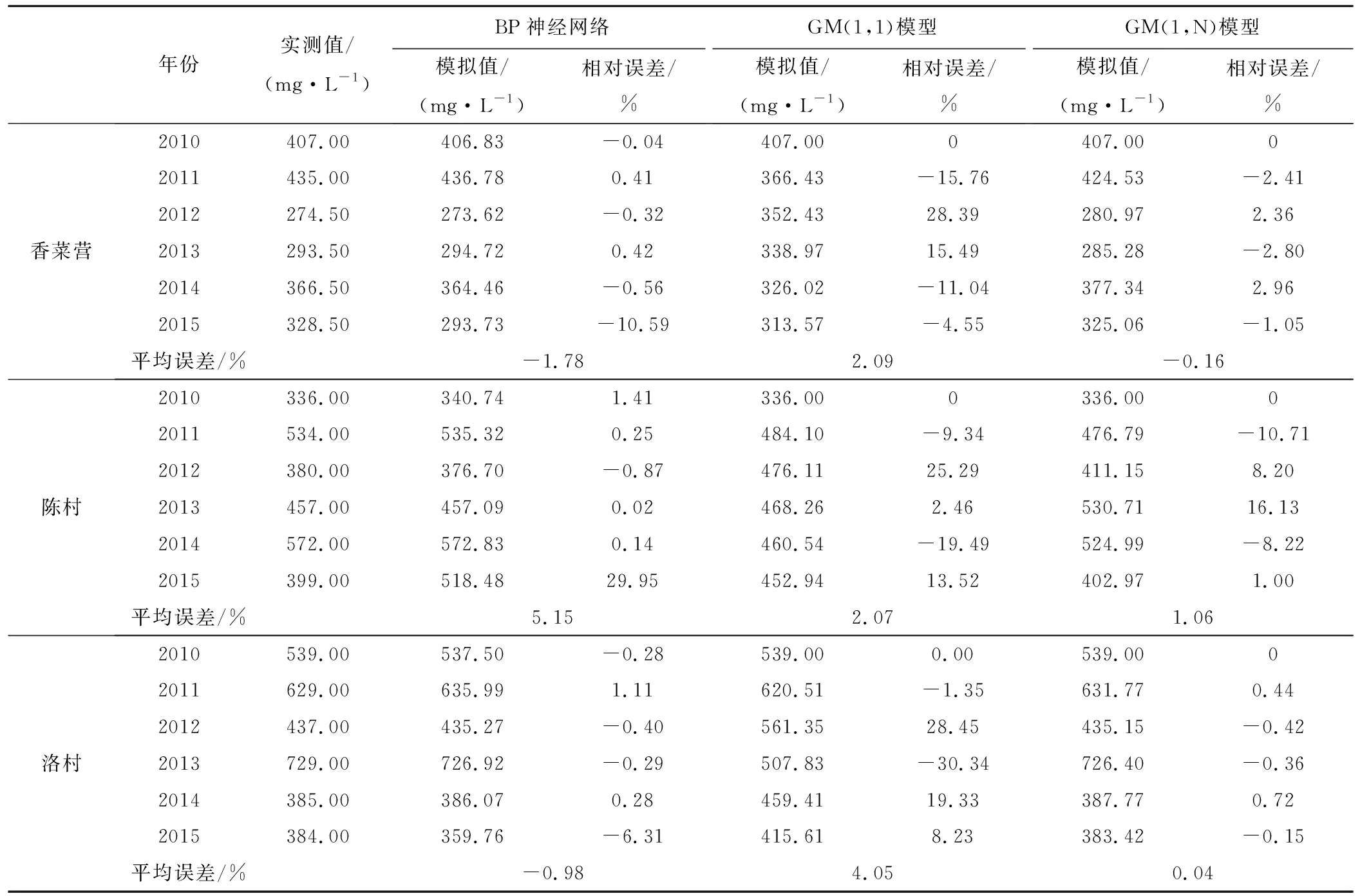
表3 监测井各模型模拟结果与实测值对比表Tab.3 comparison of simulation results and measured values of each model in monitoring wells

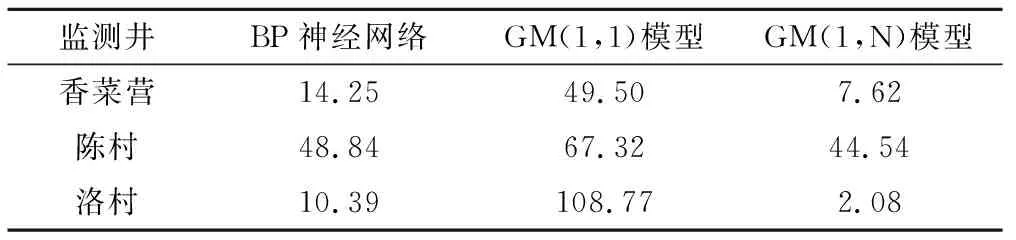
表4 3种模型的均方根误差对比表Tab.4 Comparison of RMS errors of three models

3.3 地下水矿化度预测成果

将GM(1,N)模型对临漳县地下水矿化度2016-2020年的预测结果作为最终预测成果，预测成果详见表2，由结果可知，2016-2020年临漳县三口监测井地下水矿化度整体均呈上升趋势，其中香菜营监测井矿化度于2020年达到475.58 mg/L，陈村监测井矿化度于2020年达到505.43 mg/L，洛村监测井矿化度于2020年达到501.62 mg/L。

4 结 语

本文针对邯郸市临漳县地下水矿化度问题，将GM(1,N)模型运用到当地香菜营、陈村和洛村三口监测井的矿化度模拟与预测中。以监测井水位，抽水量和区域降雨量为自变量，以矿化度为因变量，构建了基于地下水矿化度预测的GM(1,N)模型。并将GM(1,N)模型的拟合精度与BP神经网络和GM(1,1)模型的拟合精度进行了比较，结果表明GM(1,N)模型的拟合精度最高，说明该方法可以较好地应用到临漳县的地下水矿化度预测中。预测结果显示，三口监测井2016-2020年地下水矿化度变化均呈现上升趋势。该研究为邯郸市临漳县未来几年的地下水水质治理和水盐调控等工作提供了参考依据。