基于SSA-PPR模型的澜沧江枯季通航流量预测

王 超，杨绍琼，杨发瑞，周东俊，赵江艳，谢 平

(1.云南省水文水资源局，昆明 650106；2. 昆明市水文水资源局，昆明 650103；3.昆明市松华坝水库管理处，昆明 650201；4.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072.)

澜沧江是我国西南的国际河流之一，发源于青藏高原之唐古拉山北麓，国境内先后流经青、藏、滇三省。澜沧江天然落差1 768 m，水能资源极为丰富，中下游具有一定的通航能力，云南境内建有思茅港和景洪港两个港口。澜沧江素有“黄金水道”之美誉，中、老、缅、泰、柬、越等六国为之相连，全长4 900 km。由于其特殊的、重要的地理位置，发展其国际航运有利于加强我国和东盟国家的经济合作等外交关系[1]，有助于带动云南省的经济发展。

澜沧江流域主要为西南季风控制，径流主要来源于上游的冰雪融水和季风给中下游带来的降水，大气环流是影响径流变化的主要因素。澜沧江干湿季分明，5-10月为雨季，集中了77%以上的径流量。在全球增暖的大背景下，澜沧江年降水量、湿润指数均呈现震荡中下降的趋势,1951-2008年澜沧江年降水量下降46.4mm，气温约按0.15℃/10a的速度小幅上升，二者的变化对径流影响也较为明显[2,3],也是2009-2013年澜沧江流域干旱的原因之一。近年来澜沧江上的梯级水电站逐步建成，人类活动影响显著，由于梯级电站的调丰补枯，径流的年内变化幅度有所减小，对航运水量、补偿河道生态水量都有一定的调节和补充作用。

对于天然河道来讲，水深是能否通航的重要条件之一，在其他条件不变的一般情况下，河道水深与流量成正比，因此，流量是影响河道通航的重要因素之一。由于受大环流的影响对于天然河道流量一般呈现季节性变化，年内变化较大，最枯月平均流量通常只有年平均流量的几分之一甚至更少，因此，开展河道的最枯月流量预测研究，对航运保障具有重要的参考作用。

年最枯月流量，影响因子多，具有一定的周期性和较强的随机性，准确预测具有一定难度，李英晶[4-7]等学者运用多元回归、自回归模型、前后期径流相关法等对伊春河流域、密云水库等枯水季来水量预报进行了相关尝试和研究，精度基本能满足相关规范要求。年最枯月流量的预测影响因子较多，为解决个别预报因子噪声影响较大的问题，本文利用奇异谱分析技术对随机性较强的预报因子进行主周期成分重构，与其他原始因子混合后，与PPR结合形成SSA-PPR模型，对云南省澜沧江某站最枯月径流进行预测，以分析其通航保障能力。

1 SSA-PPR枯水预测模型原理

1.1 SSA分析技术

奇异谱分析，简称SSA，是对具有非线性特征的时间序列进行研究的一种行之有效的方法，它的思想是先重构时间序列的成份,然后关联经验正交函数，利用实测的时间序列，归一化后构造出轨迹矩阵，之后分解、重构轨迹矩阵，最后提取得到不同的成分和信号，并进一步识别出长期趋势、强周期和白噪声等成分，最后可对原始序列结构进行重构，目前，在各种时间序列的分析中也得到了大量应用。奇异谱分析和重构主成分，可以有效地去除时间序列中的噪声，重生序列能够较好地反映原始序列的特征[7,8]。其原理如下：

首先将所实际生产中实际观测得到的时间序列数据：x(t),t=1,2,…,n，选择适当的窗口长度：m(2≤m≤n/2)，转化为二维时滞矩阵(或轨迹矩阵)：

(1)

设其滞后协方差矩阵为S，它的特征值可表示为λ1≥λ2≥…≥λm≥0，即为{xi}的奇异谱，展开如下：

(2)

式中，i=1,2,…,N-M+1；j=1,2,…,M；Gkj为时间经验正交函数，akj为时间主分量。通过Gkj和akj进一步计算xi重建成分xkj，公式如下：

(3)

逐一对各重建分量进行分析，可识别各分量的振荡周期，并根据贡献的重要程度选择前(从大到小排)y个奇异值，使他们的贡献率之和大于一定阈值 (例如80%)，再对原序列重构，以滤除原始序列的噪声并显示原始序列的主要变化特征。

1.2 PPR技术

投影寻踪回归法(Projection Pursuit Regression，PPR)，是以直观的低维空间投影来表现复杂的高维数据，这种方法较好地解决了维数祸根和解决超高维等问题，效果较为明显。PPR应用领域日趋益广泛，特别是在水文资源、水环境等各个方面均有尝试，在洪水预报、径流预报、降水预报、水资源评估、聚类分析、水质评价等细分领域的应用均得到深入开展[9-11]。PPR建模的原理主要如下[14]:

年最枯月流量f(x)，非线性特征显著，x为预测因子，a为投影向量，二者维数均w。首先要计算得到岭函数族g(atx)。预测对象可用下式推求：

(4)

式中：g为岭函数；N为岭函数的个数。N=1、g=1时，式(4)就变为普通多元回归函数。岭函数采用Hermite多项式进行拟合，其投影回归关系式为：

(5)

式中：m表示输入样本的个数；j为多项式的阶数；c为多项式的系数；yi为在方向a上的投影；h为正交多项式(Hermite)，它们的分别表达为:

(6)

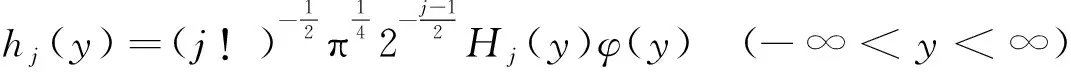
(7)

式中：φ(y)为标准高斯方程；j!代表多项式阶数j的阶乘；回归预测建模最终转化为求下式的最小化问题。

(8)

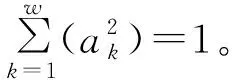
(9)

(i=1,2, …,m)

因此，投影寻踪回归预测的求解过程就转化为优选参数a、c和N。

目前，遗传算法应用最为广泛，另外，萤火虫法、差分法、粒子群法和仿生群智能算法(如蜘蛛群、蛾群、鸡群等优化算法[12,13])等也有很多探索研究，并取得了较好的效果，本文采用蜘蛛群算法确定最佳投影参数，具体步骤可参考文献[14]。

2 年最枯月流量奇异谱混合因子的投影寻踪预测建模步骤(SSA-PPR)

根据前述奇异谱分析和投影寻踪回归建模的原理，年最枯月流量预测建模的具体步骤如下。

(1)确定预测因子。利用相关分析方法确定最枯月径流的预测因子。根据所能获得的预报因子，计算最枯月径流与各种因子不同延迟时段的相关系数，选取相关系数最大且符合置信水平要求的延迟时段因子作为预报因子。

(2)对周期性较强且由于受人类活动等噪声影响较大的因子进行奇异谱分析和重构序列。其他影响因子采用原始观测因子作为预报因子。

(3)按照文献[14]用群居蜘蛛算法确定最佳投影参数，得到最终投影寻踪回归模型及模拟和预测结果。

(4)根据水文情报预报规范(GB/T 22482-2008)对最枯月径流预测结果进行评价。

3 澜沧江枯节通航流量预测模型构建与检验

本文选取澜沧江某站受人类活动影响较小的1957-1999年共43年资料进行验证，其中，1957-1994年共38年为训练期，后面5年为检验期。澜沧江某站最枯月径流多出现在每年2月，故以2月平均流量作为预报对象。当预测的2月平均流量低于澜沧江通航最小流量时，将无法正常通航，需通过一定的调度进行保障。

由于在该流域及其附近缺少全面的气象资料，所以大气环流方面的资料仅能从相近地区收集而得，23个气象因子名称见表1。

根据澜沧江流域2月份天气系统物理方面的成因，分析各因子的位置及影响范围，结合本流域与各因子的物理关系选取相应的预报因子，首先从物理成因方面对各个影响因子进行考察，通过考察后，为了使各预报因子与预报对象相关性更好，采用相关系数法逐一对因子进行筛选。采用计算机智能挑选的方法确定各预报因子的提前期。置信度a取0.05，阀值Ra=0.31，相关系数小于0.31的因子予以舍弃。

为提高回归分析的预测效果，在综合平衡的前提下，将独立性较差(相关性较好的一对因子其中之一)的因子去掉。最终选定的影响因子为因子2、因子4、因子9、因子19、因子20和因子23，同时，由于汛期5-10月份径流对后期最枯月径流影响较大，与预报对象2月份平均流量相关性较好，故将其纳入作为影响因子。由于汛期5-10月份径流受水利工程开发、调度等人类活动影响较大，数据白噪声也较大，因此采用SSA方法对其进行主成分重构，选取累积贡献率达85%的前10项对其重构，以消除其白噪声的影响，原始序列与重构序列对比见图1。

表1 预报因子序号、名称对照表Tab.1 Forecast factor's number, name comparison table

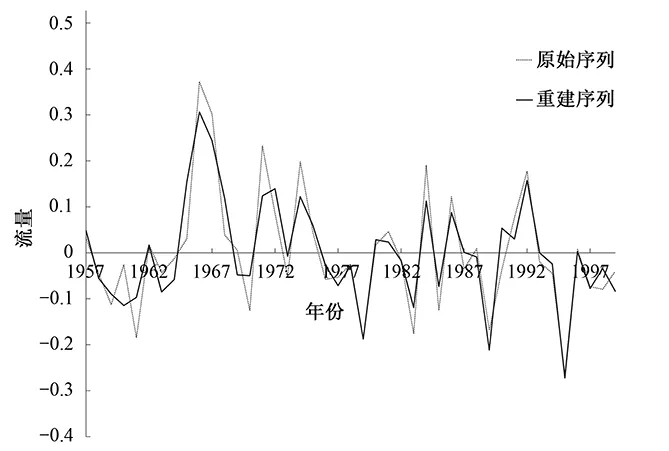
图1 影响因子(汛期径流量)原始序列与重构序列对比图Fig.1 Influence factor (Runoff of flood season) comparison between original sequence and reconstructed sequence

通过对比可以看出，SSA重构前后汛期径流量趋势一致性较好，由于去除了白噪声等随机性的影响，重构之后的序列变化更加平稳，变幅略有变小。

为验证奇异谱分析前后对预测结果的影响，分别将因子2、因子4、因子9、因子19、因子20、因子23、汛期5-10月份平均流量原始序列，因子2、因子4、因子9、因子19、因子20、因子23、奇异谱分析重构的汛期5-10月份径流序列两组因子分别用模型进行模拟和预测，详见表2。

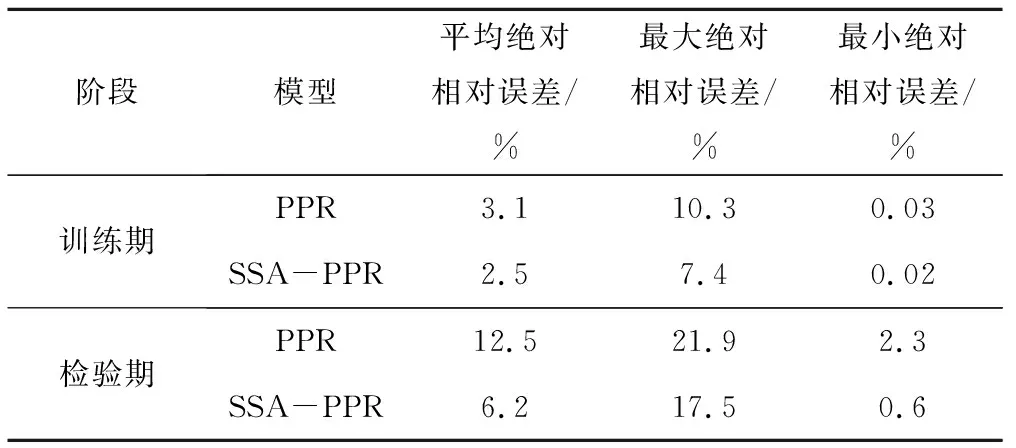
表2 PPR模型和SSA-PPR模型预测结果对比Tab.2 Comparison of Predicted Results

结果表明：澜沧江训练期和检验期SSA-PPR模型的平均绝对相对误差、最大绝对相对误差、最小绝对相对误差三者均较PPR模型小，说明SSA-PPR模型模拟和预报精度均较PPR模型高。SSA-PPR模型训练期平均绝对相对误差、最大绝对相对误差、最小绝对相对误差分别为2.5%、7.4%和0.02%，检验期分别为6.2%、17.5%和0.6%，检验期预测精度低于训练期模拟精度。

根据PPR模型和SSA-PPR模型模拟和预测过程对比可以看出，SSA-PPR模型模拟和预测过程与实测序列过程更为吻合，起伏过程一致性更好，同时预测结果与实测过程均显示总体呈现一个缓慢下降的趋势，与有关学者研究结论基本一致[19,20]，详见图2。

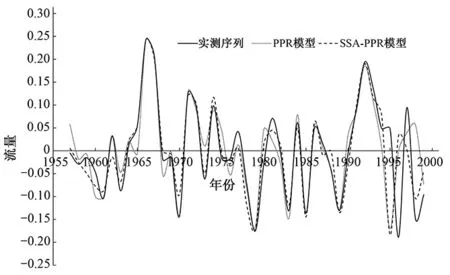
图2 PPR模型和SSA-PPR模型预测过程对比图Fig.2 Comparison of Prediction Process between PPR Model and SSA-PPR Model

按水文情报预报规范(GB/T 22482-2008)评定标准[15]，SSA-PPR模型预报总体合格率为88.7%，综合精度评价为甲等。总体上看SSA-PPR模型所预测的澜沧江某站年最枯月流量精度满足要求，效果较好。

上述成果经过训练期与检验期检验分析有一定精度，但也主要基于不同要素的时间序列分析而得，因子之间物理联系不明确，其成果存在一定不确定性。目前，澜沧江流域由于受多级水电站影响，且各级电站水位、出入库流量等监测信息还未统一报送，因此还暂时不具备构建流域水文模型的条件。在条件成熟时应构建水文模型，在多种方法相结合的基础上综合分析，进一步提高预测成果可靠性。

4 结 语

为解决澜沧江枯季通航能力预测实际问题，从影响枯水径流的因子及枯水径流序列出发，提出了将影响因子与经过奇异谱重构的径流周期因子相混合，并利用投影寻踪回归对澜沧江枯水径流进行预测；根据云南省某站(1957-1999年)的年最枯月流量资料预测，结果表明：

(1)天然河道径流量是影响澜沧江通航的重要因素之一，由于受大环流的影响季节性强，年内变化较大，开展澜沧江的最枯月径流量进行预测研究，对航运保障具有重要的参考作用。

(2)训练期和检验期SSA-PPR模型的平均绝对相对误差、最大绝对相对误差、最小绝对相对误差三者均较PPR模型小；SSA-PPR模型模拟和预测过程与实测序列过程吻合更好，SSA-PPR模型预测效果总体更优。

(3)SSA-PPR模型训练期平均相对误差绝对值为2.5%，预测期平均相对误差绝对值为6.2%；预报合格率较高，为88.7%，按预报标准评价其精度为甲等。SSA-PPR模型所预测的澜沧江最枯月流量精度达到要求，可供澜沧江枯季通航流量预测和调度使用。

(4)笔者提出SSA-PPR模型，在传统的多元回归基础上为枯季通航流量预测增加了一种方法，但由于受水利工程调度的影响，实际工作中还要结合短期的预报对成果实时进行修正，各部门应加强澜沧江流域梯级电站水文信息共享建设，为构建物理意义明确的流域水文模型创造条件，对预报的实际效果不断验证并对方案逐步完善，提高预报成果的确定性，以满足实际工作的需要。