应用PSO-KELM模型预测水文时间序列

涂 异，汪金能，朱曲平，安雪玮，梅 艺，陈东祖

(重庆工程学院土木工程与建筑学院，重庆 400000)

水文水资源及水利工程中，有大量问题涉及时间序列，如径流量预测、蒸发量预测等。而这些问题正是水利工作者决策时所需参考的关键因素之一[1,2]。

有大量数学方法被引入水文时间序列预测之中。如周秀平等[3]应用最小二乘支持向量机进行年径流量预测，并通过马尔科夫链对模型计算结果进行修正，进而组合得到最终结果；蒋晓辉等[4]提出了径流预测的混合回归模型，将该模型应用于黄河三门峡站年径流量预测之中，并取得了较为满意的应用效果；覃光华等[5]采用小波方法对径流序列进行分解，以获取其确定性项和随机项，尔后采用广义回归神经网络再次建模，建立了WA-GRNN组合模型，并将该模型应成功应用于沱江中上游三皇庙水文站年径流预测之中；崔文东[6]将神经网络用于径流预测中，同时比较了单隐层BP神经网络、多隐层BP神经网络、RBF网络和GRNN网络的应用效果，结果表明后三者都能取得较前者更好的结果。另外，还有灰色理论等诸多数学模型被用于水文时间序列的预测之中[7]。

由上述可见采用数据驱动建模进行水文时间序列预测是目前的一种较为可靠的方法。极限学习机是一种典型的数据驱动建模方法，其实质上是一种单隐层神经网络，网络的结构特点决定该方法具有运算速度快的优点，目前已在滑坡位移预测、风力预测等工程领域得到了一定应用。但标准极限学习机也存在一些缺点，如其前馈层网络权值仍需随机给定，一定程度上降低了该方法的稳健性。针对上述不足，一些修正极限学习机的方法如核极限学习机也被陆续提出，大大改善了其原有的性能[8-9]：最为典型的即是参照最小二乘支持向量机(LSSVM)的特点，将核方法引入极限学习机中，即核极限学习机(limit learning machine with kernel function, KELM)。研究表明核极限学习机能够取得更优于LSSVM的结果。但由于核函数有多种类型，典型的有RBF核函数和多项式核函数，选择不同的核函数对模型结果具有较大的影响。从目前的研究上来看：融合多种核函数的混合核函数方法能够获得较为满意的结果。

鉴于上述分析，本文拟提出一种水文时间序列预测的新方法，即混合核PSO-KELM模型。应用兰州站年径流量和金沙河流域年径流量实测数据验证新方法的合理性。

1 混合核PSO-KELM模型

1.1 模型的构建

极限学习机[8](ELM)是一种简单、有效的单隐层前馈神经网络。因其结构简单，易于实现，已在工程领域得到了一定应用。与BP模型不同，ELM模型无需对网络中的连接权值进行迭代调整，仅通过设置网络的隐含层节点数量就能够通过解析计算得出网络的输出权值，因此拥有计算速度快和泛化性能好的优点。

尽管ELM方法拥有上述众多优点，但由于其输入权值和隐含层偏差是在网络初始化时随机产生的，在一定程度上导致了算法输出权值的不稳定[9]。为此KELM通过引进核函数替换ELM算法中原有的随机映射函数，改善了ELM方法输出权值不稳定的缺点[9]。给定训练数据p，其期望输出值表示为t。按照标准优化的观点，KELM的训练函数可表示为：

(1)

其中，ξ=[ξi,1,ξi,2,…,ξi,m]T表示样本xi的模型实际输出与期望输出的误差；β是隐含层与输出层节点间的连接权值；C表示惩罚系数；h(xi)为训练样本xi的隐含层输出值。根据KKT理论，可以将式(1)等效为式(2)：

(2)

式中：αi,j是Lagrange乘子；βj为连接隐含层和第j个输出节点之间的权值向量，且β=[β1,β2,…,βm]。据KKT优化条件，有：

(3)

其中，ai=[ai1,…,aim]T,a=[ai1,…,aiN]T，再对式(2)进行求解，整理得到如下表达式：

(4)

根据Mercer条件，定义KELM 的核矩阵为：

Ω=HHT:Ωi,j=h(xi)·h(xj)=K(xi,xj)

(5)

则KELM模型的输出表达式为：

(6)

通常认为，满足Mercer条件的函数即可作为KELM的核函数。按照多核学习的思想，定义混合核函数[10,11]如下：

K=aKpoly+(1-a)Krbf=

(7)

构造的混合核函数K结合了全局函数多项式核函数Kpoly和局部函数RBF核函数Krbf的优点。a表示Kpoly和Krbf之间的调节系数，当a趋向1 时，此时的K的功能就偏向于Kpoly；同理，当a趋向于0时，K就偏向于Krbf。

对式(7)进行分析，可知需对式(7)中3个变量δ、q、a优选，而上述的惩罚系数C也可用优化方法进行寻优[11]。则混合核KELM的求解问题可归结为关于四个变量的优化问题，即x=[C,δ,q,α]。目前，解决这类问题的一个有效方法是运用智能算法进行寻优。其中，智能算法包括遗传算法(GA)、粒子群算法(PSO)、人工蜂群算法(ABC)等，本文选择最易实现的PSO算法优化混合核KELM的四个参数。PSO算法的核心是粒子更新速度和位置，即[12]：

(8)

式中：w表示惯性权重，通常取值从0.9到0.4递减；c1、c2表示学习因子，通常取值均为2；r1、r2表示两个随机数。

应用PSO算法对混合核KELM的待优化参数x=[C,δ,q,α]进行寻优，选用适应度最佳的一组参数作为混合核KELM模型的参数，其中适应度的计算公式如下：

(9)

1.2 模型的进一步分析

由上述分析可见，PSO-KELM模型本质上也是一种黑箱模型，即其建模机理是基于数据驱动，故该种模型具有普适性，只需要求数据样本不能过少。正如引言所指出，这类基于数据驱动的建模方法擅长处理非线性问题。而与其他数据驱动建模方法，如BP神经网络模型、RBF模型相比，新模型在稳健性上有了较大的改进，这主要是新模型避免了随机产生输入权值和隐含层偏差的不足。另外，新模型综合了核方法的优点，使用径向基核函数和多项式核函数相混合的方式，这能够最大程度的保证模型的稳健性。下文将以实例验证，对比新模型和BP神经网络模型、RBF模型的应用效果，以检验模型是否合理。

2 工程实例

2.1 兰州站年径流量实例预测

本文以兰州站年径流量预测为例，检验PSO-KELM是否有效。兰州站1955-1982年年径流量实测数据见图1[7]。取1995-1977年的实测数据用于训练模型，以获取模型结构参数，后5年的实测数据用于检验模型，作为对比，同时和水文时间序列中采用较多的BP模型进行径流预测，以比较两者方法之优劣性。PSO-KELM模型和BP模型的预测结果见图2。本文所有计算结果均由MATLAB实现。

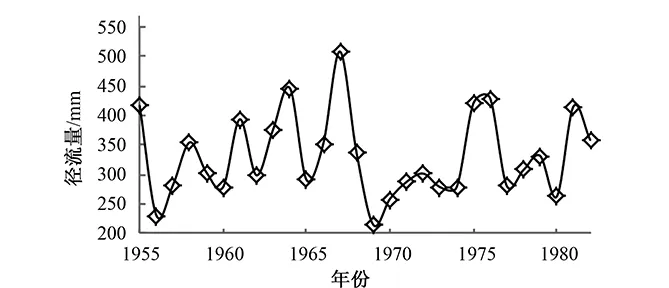
图1 兰州站1955-1982年年径流量实测数据Fig.1 Measured data of annual runoff of LanZhou Railway Station in 1955-1982

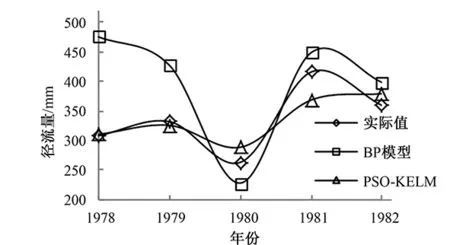
图2 模型预测结果比较Fig.2 Comparison of model prediction results

两种模型的相对误差统计见表1：在1978～1980年间和1982年，显然PSO-KELM模型精度高于BP模型，而在1981年，PSO-KELM模型精度低于BP模型，这可能与样本的分布有关，这也是数据驱动建模的特点，即预测结果取决于样本质量。但从整体误差统计上分析，无论是最大、最小、平均误差，PSO-KELM模型精度都优于BP模型。

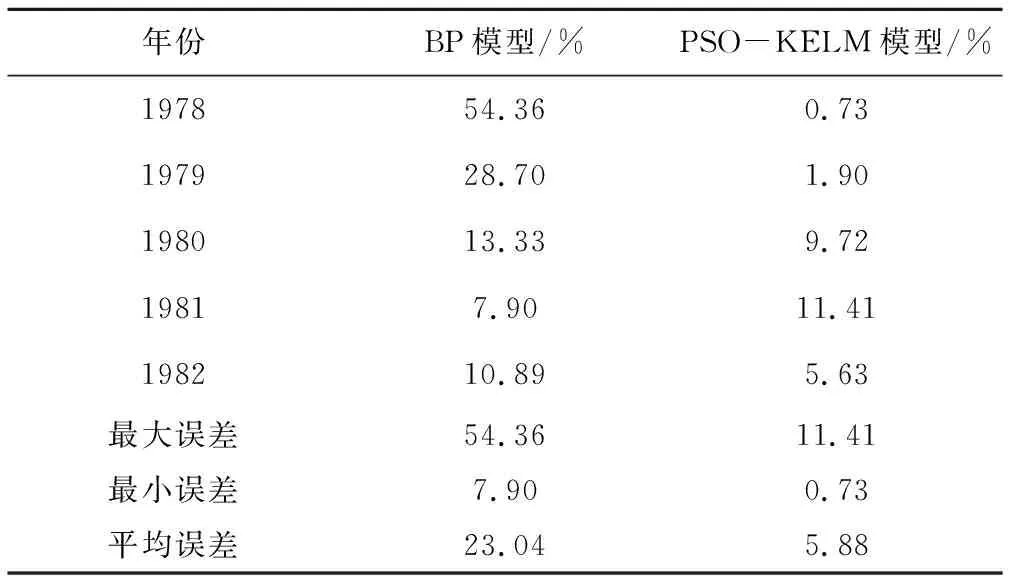
表1 两种模型的相对误差Tab.1 Comparison of model relative error

2.2 金沟河流域年径流量预测

以位于金沟河流域的八家户站年径流量实测数据进一步检验模型有效性。金沟河流域1957-2003年年径流量数据见图3所示[13]。以1957～1995年的实测数据进行建模，1996-2003年的数据用于检验模型。作为比较，同时计算了BP模型和RBF模型的结果，三种模型的比较见图4。

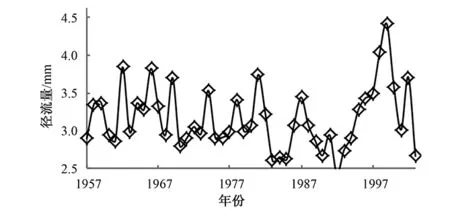
图3 金沙河流域1957-2003年径流量实测数据Fig.3 Measured data of annual runoff of Jinsha River Basin in 1957-2003

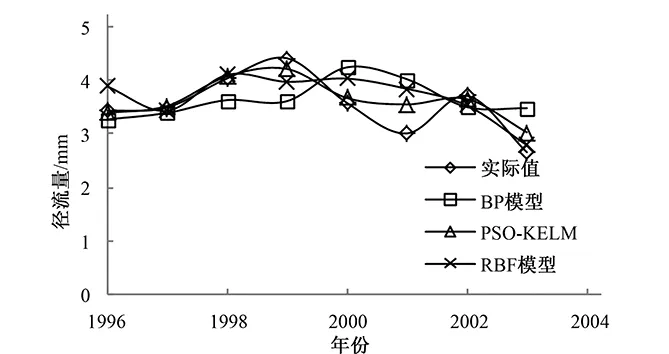
图4 模型预测结果比较Fig.4 Comparison of model prediction results

三种模型的预测相对误差对比见表2，可见除2003年外，PSO-KELM模型的预测结果都优于前BP和RBF模型。仍然从整体误差上分析，由表2可见，整体预测性能PSO-KELM模型最优、其次为RBF模型、BP模型的性能最差。

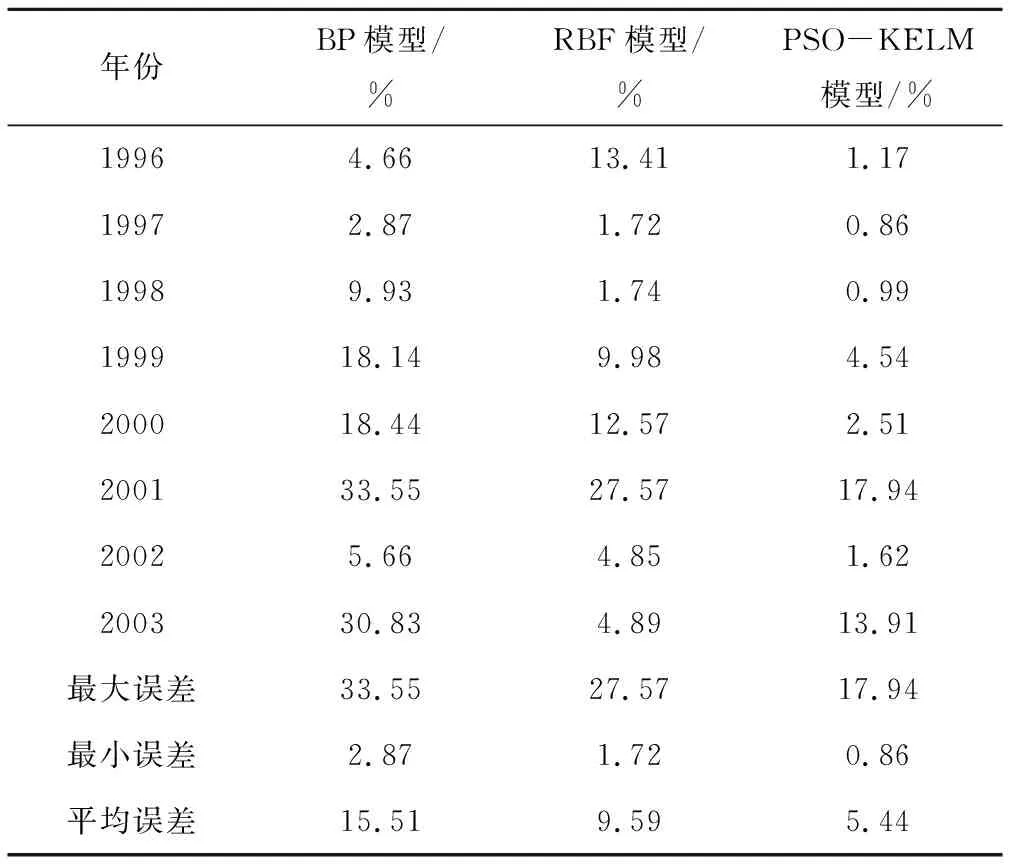
表2 模型的相对误差Tab.2 Comparison of model relative error

需要说明的是，在复杂性程度上，PSO-KELM模型与BP和RBF模型相比，既省却了繁琐的网络训练过程，又保证了预测准确度；而与ELM相比，增加了核函数参数搜索的步骤，但由于采用PSO算法进行搜索，可较为快速的获取到最优参数。同时，由于PSO-KELM避免了ELM可能存在的结果不稳健的缺点，在实用性上更强。而与LSSVM(该模型同样存在参数，也需要通过优化算法获取最优参数值[14])等模型相比，新模型能够在同等精度的条件下拥有更小的计算量。据此可判断：PSO-KELM模型应用于水文时间序列预测是可靠的。

3 结 语

基于数据驱动建模方法，以典型的水文时间序列为例，研究所提出方法的合理性，取得结论如下。

(1) 提出了一种预测水文时间序列的混合核PSO-KELM模型：按照多核学习思想，将典型的全局核函数(多项式核函数)和典型局部核函数(RBF核函数)加权得到混合核函数，代入极限学习机模型中，并通过PSO算法获取最优的模型参数，进而实现水文时间序列的预测。

(2) 通过兰州站年径流量预测实例表明：PSO-KELM模型的平均误差较BP模型大大减小；通过金沟河流域年径流量预测实例表明，PSO-KELM模型的预测精度要高于RBF模型和BP模型。同时PSO-KELM模型省却了BP模型等存在的繁琐的网络训练过程，便于工程应用。

(3) 实例分析中表明，PSO-KELM模型仍然具有一定的误差，这可能是样本量造成的。故建议在实际应用中增加更多的样本训练以保证模型准确度。