基于静气弹修正的亚音速大展弦比飞机疲劳载荷计算研究
郭天天, 王 天
(航空工业西飞设计院 结构强度所,陕西 西安 710089)
引 言
飞机疲劳载荷主要用于估算机体结构的使用寿命和进行疲劳可靠性分析,为最终设计阶段的全机及部件疲劳试验做准备。在飞机飞行过程中,作用于机体结构上的实际载荷就称之为疲劳载荷。编制飞机疲劳载荷谱时必须以飞机疲劳载荷作为编制基础。
疲劳载荷计算主要包括计算情况的确定、计算模型的建立、计算方法的选取、原始数据的准备等,其准确度直接决定飞机结构的疲劳强度和疲劳寿命。亚音速大展弦比飞机(机翼、平尾和垂尾等)主翼面是飞机结构的主要承力和传力部件,其设计技术是飞机设计关键技术的核心,对飞机的安全性和经济性有重要影响。现代飞机主翼面结构主要承受气动载荷、发动机推力(或拉力)载荷及惯性载荷作用,机体结构柔性大大增加,所以翼面载荷设计必须考虑弹性变形的影响。
弹性变形翼面气动力分布载荷的修正是指考虑机翼弯曲和扭转变形对机翼气动载荷影响的修正技术,对于大展弦比翼面结构飞机,其载荷在飞行状态时复杂程度最高,同时飞行状态下飞机气动载荷分布将会受到其结构弹性变形的显著影响,《中国民用航空规章》第25部R4版[1](CCAR-25-R4)§25.301(c)条款规定如果载荷作用下的结构变形会显著改变外部载荷或内部载荷的分布,则必须考虑这种载荷分布变化的影响,因此,弹性变形翼面气动力分布载荷修正方法的研究是对气动分布和结构变形耦合情况下的载荷重新分布做计算分析。
这种工程方法以风洞试验为基础,根据《飞机设计手册》第9册[2]和《中国民用航空规章》第25部R4版中的计算理论和适航条款,对于刚性体飞机,在修正结构弹性变形所带来的气动载荷分布影响时可采用亚音速稳定常流的改进二元升力线理论配合以风洞试验方法,计算出压力分布的刚性影响,借助于线叠加原理对部件载荷的分布加以确定,即可随之计算得知飞机各部件的剖面载荷。上述计算方法将风洞试验数据和气动理论进行了统一,多年的实践检验和载荷测量试飞验证表明该方法具有较高的计算精度,适用于亚音速大展弦比结构飞机。
本文以某亚音速大展弦比结构飞机为例,将机翼疲劳载荷计算结果与载荷谱飞行实测进行了对比分析,得出了相关结论。
1 载荷计算情况
疲劳载荷计算情况的确定原则首先是要保证此种情况在整个飞行过程中是可能出现的,其次是要选取足够多的情况以保证每一部件的严重受载情况不被遗漏。相较于静载荷计算,疲劳载荷计算最大的不同之处就在于载荷计算情况的差异。
静载荷计算情况是基于飞行包线的边界,其飞行参数大多数是飞机的极限值,同时还需要将计算结果乘以安全系数来保证飞机足够的安全性;而疲劳载荷计算是确定飞机在正常使用状态下的载荷,其峰谷值要根据实测参数的统计规律来确定,每个任务段的典型飞行参数是各任务段的中值,这些值要远小于其飞行极限。疲劳载荷计算结果不需要乘安全系数,因此,疲劳载荷计算情况与静载荷计算情况的不同决定了疲劳载荷在数值上远小于静载荷。
飞机在正常使用过程中每一时刻的飞行参数都不相同,无法给出飞行过程中的载荷随时间的变化历程,首先是由于燃油质量和装载方案以及飞机飞行状态参数存在不确定,然后是飞机在飞行过程中受到突风受载情况等随机性。这些情况都决定了不可能给出整个飞行过程中每一时刻的疲劳载荷。所以必须基于飞行情况简化统计规律,把飞机飞行情况分成诸多任务段,以具有代表性的质量数据以及飞行参数对各个任务段飞机飞行情况加以替代,在每一任务段中给出载荷的变化,就可以确定出该任务段的载荷谱。而每一任务段的载荷变化也是一个随机过程,无法事先确定,只能根据统计规律确定。同时由于在飞行过程中不可能对所有部件载荷进行统计,因此需要建立起飞机部件载荷和飞机某一统计参数的关系,有了这种关系就可根据此统计参数的变化规律确定出载荷的变化规律。飞机飞行过程中重心的过载最容易获得,同时过载又是所有部件载荷的集中体现,因此飞机部件疲劳载荷计算通常是将部件载荷与飞机重心过载相联系,假定每个任务段各部件载荷随飞机重心过载线性变化,则只需确定飞机各部位的1g情况以及每g情况载荷,即可根据飞机重心处过载的变化对各个部件不同任务段载荷的变化情况加以确定。总的来说,疲劳载荷计算的就是飞机各部件的1g载荷和每g载荷。当然对于飞机部件在某些情况下的载荷变化可能与飞机重心处的过载变化关系不大,即过载变化以不能正确反映载荷变化,如偏航机动时的垂尾载荷和方向舵载荷,此时应建立部件载荷与另一统计参数的变化关系。如在偏航机动时给出单位舵偏的载荷增量就能根据舵偏角的统计规律确定偏航机动时飞机部件的载荷变化,这里不再讨论。
综上所述,疲劳载荷计算情况根据飞机疲劳飞行剖面和飞机自身的受载特点确定,飞行任务的差异事实上是源于飞机装载方案以及燃油质量存在差异,将飞机飞行任务分为多个任务段飞机能够确定飞机飞行的受载形式。
2 载荷计算过程
2.1 计算方法
首先根据飞机典型飞行剖面确定疲劳载荷计算的载荷情况,然后根据飞行剖面中对应的飞行质量、飞行速度和受载情况确定飞机在该任务段中的飞行参数,即全机过载、攻角、侧滑角和转动角加速度等飞行参数,并依据风洞试验数据及弹性修正计算出弹性飞机在此飞行参数下的气动载荷,再根据其质量特性数据对飞机在该飞行参数的惯性载荷加以计算,最终把气动载荷与惯性载荷叠加即可得到机身机翼各站位总载荷。
2.2 计算模型
在载荷计算中,对于亚音速大展弦比飞机,可根据前文介绍的载荷计算方法建立载荷计算模型。根据《空气动力学》[3]中的机翼低速气动特性,采用改进的二元升力线理论计算翼面气动力。将其沿弦平面方向顺气流分成为一系列梯形气动分块而弦向则不处理,并在气动分块弦线的1/4线处布马蹄涡用于模拟升力,结构模型为截面刚度随位置变化的单梁结构。对细长体结构(包括机身、短舱等)进行了简化,简化成为曲轴旋成体,同时将其体表分为一系列的三角以及四边形气动力分块,其上部气动面元用于模拟细长体厚度效应和翼身气动干扰,以机身和发房为例,计算时其作为翼面的气动分块之一参与气动分布载荷计算。
2.3 计算理论
参考《民用飞机载荷计算研究与软件研制》[4]中的计算理论,如下图1机翼平面示意图,对翼面进行划分,将其分为m(图1中m=4)气动分块,各个分块弦线的1/4处布置如下的马蹄涡,以其代替翼面各气动力分块的升力。对于其中之一,假定马蹄涡所在剖面二元升力线正切值为m0,升力为l。

图1 机翼平面马蹄涡布置
基于库塔—儒可夫斯基升力定理,二维翼型存在如下公式:
l =ρVΓ
(1)
(1)式中: ρ表示当前高度下标准大气密度;
V表示的是飞机的真空速;
Γ表示的是直线涡元的环量。
此外,基于亚音速线性化理论:
(2)
(3)
在(2)和(3)式中:
αf表示机体轴线相对气流方向的迎角;
wr表示与涡量相切的曲线对距其r处所具有的诱导角速度;
c表示与机体对称面平行的当地气动弦长;
r表示诱导角速度所在之处与涡核的间距。
由(1)和(2)可得
(4)
将(4)式代入(3)式可得
(5)
将控制点选在3/4弦长处,即r=c/2时有:
(6)
对于大展弦比的机翼若考虑m段升力,则式(6)以矩阵方式表示为
(7)
上式中:
{ }为列矩阵;

由图1马蹄涡布置可对马蹄涡对控制点诱导速度进行如下推算:
(8)
上式(8)种[S1]矩阵表示气动影响系数矩阵,后文将对其进行导出。
式(1)、式(8)联立可得下式(9):
(9)
上式中q为速压,q=ρV2/2。
由方程(9)和(7)有
即飞机在对称飞行过程中及机翼各分块气动力{l}可做如下表达:
(10)
式中:
[S1]表示气动力影响因子矩阵,其矩阵形态仅受翼面几何外形影响;
q表示的是飞机的当地动压;
mo表示的是翼面处的二元升力线正切值;
αf表示机体轴线相对气流方向的迎角。
式(10)中,以mo表示二元升力线正切率而非以2π加以表示,其主要原因在于压缩性考虑以及利用真实风洞试验数据两方面。
式(10)中,可通过风洞试验数据逆向推算得到mo。而由于气动影响矩阵[S1]仅受机翼平面形状影响,只要知晓平面形状即可推算[S1],所以只需求得各剖面零升力线攻角αf,即可计算得知展向升力分布{l}。
式(10)为机翼翼面气动力求解方程,假定各任务段涡单元流动为二维剖面流动,倘若各翼剖面处mo和αf值为已知,即可推导出机翼翼面气动分布。下述三部分组成了各翼剖面实际攻角αf:
{αf}={αr}+{αs}+{αg}
(11)
在式(11)中,{αr}表示的是翼根弦线相对气流的迎角,{αs}表示气动分布载荷导致飞机机翼剖面弹性扭转而出现的翼弦线迎角增量,其随翼剖面的气动载荷{l}线性变化,如下(12)所示:
{αs}=[S2]{l}
(12)
矩阵[S2]表示的是机翼弹性影响系数矩阵,其受到飞机机翼刚度影响。
在式(11)中,{αg}迎角增量产生的主要原因为控制面偏转、机体滚转以及机翼扭转、气动载荷干扰扭转等导致的机翼结构变形;次要原因为机翼结构惯性载荷、外挂物的作用力等导致的翼面结构扭转。
工况设计已有的条件通常是飞机的质量以及使用过载,所以增加了两个力和力矩的平衡方程,其一为式(13)所示的力平衡方程:
2[2h]{l}+pT-nW=0
(13)
其二为式(14)所示的力矩平衡方程:
-2[2hx]{l}+2q[2hc2]{cmo}-pTxT+nWxT=0
(14)
式(13)和式(14)中:
h表示的是二分之一涡宽;
PT表示的是水平尾翼的平衡力;
n表示飞机重心处垂向过载,向上为正;
W表示的是全机质量;
x表示的是飞机力矩参考点与机翼涡升力作用点的间距;
Cm0表示的是翼剖面零升俯仰力矩系数;
xT表示的是飞机力矩参考点与平尾平衡力作用点的间距;
[ ]表示为行矩阵。
(10)、(13)、(14)式即为飞机在对称飞行工况下计算气动力分布的三个基本方程。
通常情况下,由于机身、发动机短舱和机翼气动力之间存在相互干扰,通过Ted L. Lomax[5]飞行载荷计算方法,可以得到下面的方程:
(15)
其中: [I]表示的是单位矩阵;
[D]表示发动机短舱干扰系数矩阵;
[Si]表示的是机身气动力镜像涡系数矩阵;
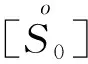
αi表示的是飞机机翼安装角。
式(15)是表示飞机对称飞行工况的基本方程。从形式上而言,反对称飞行基本方程的形式与之呈现一致性,其差别仅仅在于气动力影响系数矩阵[S1]的量值差异。此外,需要考虑副翼偏角与滚转角速度的变化对机翼迎角增量的影响。由于前二者与后者之间存在线性关系,因此可先对单位舵偏与角速度变化导致的各机翼剖面零升迎角的增量进行计算,其后再基于二者实际值对瞬时的机翼迎角增量加以计算推导出反对称工况下的机翼升力分布。
不论飞机处于何种飞行情况,都可将其分成对称情况和反对称情况,其后采取分别求解、结果叠加的方式计算出该情况下飞机的总载荷。
2.4 理论及技术创新点
目前,国内各飞机设计所对于气动力的弹性修正已经基本掌握并用于实际型号设计中,相对于传统的疲劳载荷计算方法,我们以《飞机设计手册》第9册和《中国民用航空规章》第25部R4版为设计规范,使用计算机FORTRAN语言自主编制研发而成了一套完整的计算程序。在国内首次将亚音速稳定常流改进的二元升力线理论和风洞试验数据结果相结合,并借助于融合后的方式对静气弹予以修正,同时基于刚性飞机全机气动分布的刚性影响进行了计算,结合线叠加原理对全机所有部件气动力分布加以确定,最终推算得出剖面载荷。多年实践检验和载荷测量试飞验证表明,该方法具有较高的计算精度,适用于亚音速大展弦比结构飞机。
在计算过程中通过载荷计算代码结合程序中的判断模块识别疲劳载荷计算剖面及工况,使用数据集管理系统存储和处理原始计算数据,当载荷计算过程中需要对数据文件进行调用时,只需直接调用数据集中对应的数据文件即可,并可按照相应的计算代码按需打开和读取对应的数据文件,无需逐一调用。此方法在国内也属于首次尝试,并已成功申请国家发明专利。
3 载荷计算实测验证及对比分析
根据《飞机结构载荷/环境谱》[6]一书中飞机飞行载荷谱实测以及编制部分,对于机翼,可粘贴应变片于各实际测量剖面,借助于载荷地面标定构建应变与载荷的实际对应,即可推算飞机部件的实测载荷。实测载荷能表示出飞机载荷时间历程,然而因为数据采集量大,加之飞机改装存在较大困难,因此载荷测量剖面选择数量有限,需要通过计算方可推算出其他部位的载荷,载荷测量的作用仅在于对计算准确性进行验证。
为验证本方法的可行性,以某亚音速大展弦比飞机为例,对飞行实测数据和机翼疲劳载荷计算结果进行了对比分析。
首先,参考《飞机结构疲劳定寿文集》(第一集)[7],按照实际情况,将该型飞机分为训练飞行和航线飞行两个飞行任务段,同时将各任务段分为飞行和地面两种。其中,飞行情况又可分为多个小任务段,同时也可根据受载形式将其分成机动以及阵风等工况,表1为该型飞机任务段参数。因为在全机质量分布、商载和飞参等方面,载荷谱飞行实测与计算采用的飞机参数存在一定差异,为方便与飞行实测数据进行对比,计算了训练飞行中接近的飞行质量以及装载各任务段载荷测量点的载荷,给出了右机翼三个测量剖面附近的1g载荷和每g载荷。计算数据详见《MA60飞机疲劳载荷计算研究》[8]。

表1 某亚音速大展弦比飞机飞行剖面参数
然后,载荷谱实测时选取了和计算参数接近的1g工况载荷,同时按照机动及阵风等工况对飞行实测的每g载荷进行计算,获得了计算与实测的载荷对比,实测数据见《飞机机体载荷谱飞行实测与数据处理》[9],对比分析结果见表2,力的单位为千牛(KN),力矩的单位为千牛·米(KN·m)。
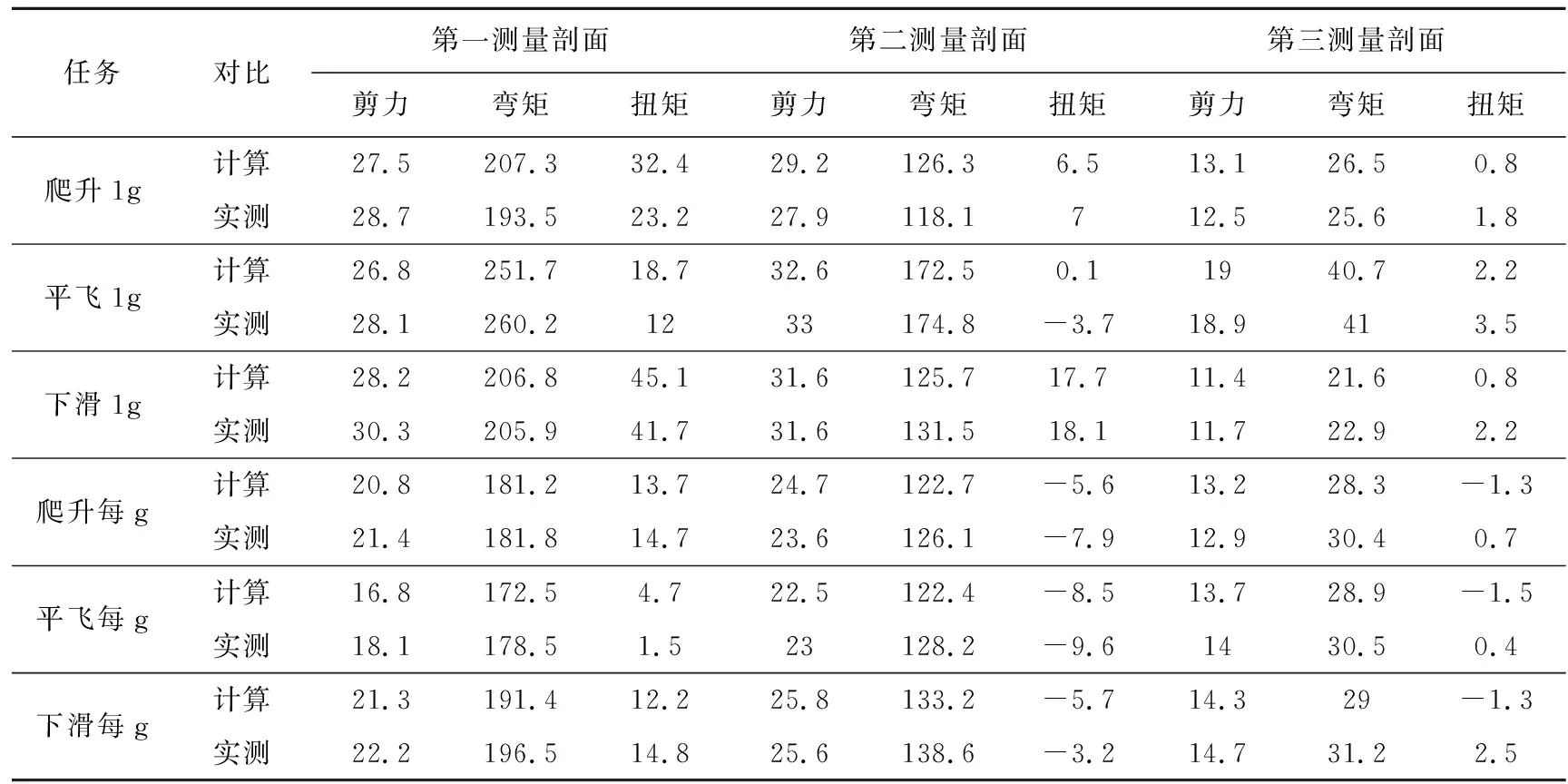
表2 某亚音速大展弦比飞机计算载荷与实测数据对比
通过表2计算载荷与实测数据的对比分析可以得出:剪力及弯矩的误差范围基本在10%以内,而扭矩由于量级较小容易引起较大相对误差,为便于弹性变形修正计算,机翼沿弦平面仅有1个气动力分块,因此难以精准模拟静气弹变形时的弦向气动力。同时实测飞机瞬时质量、重心以及飞行参数与载荷计算相同也将导致扭矩计算误差。然而因为扭矩自身量级较小,基本不会显著影响到结构疲劳寿命。以上对比分析验证了本疲劳载荷计算方法的准确性。
4 载荷计算结果及分析
下面对各任务剖面机翼疲劳载荷数据进行分析说明,计算结果详见《某型飞机疲劳分析用全机疲劳载荷计算》[10]。
训练飞行1g和航线飞行1g时机翼各肋弯矩的计算结果分别见图2和图3。1g载荷情况下各个飞行任务段计算速度存在差异,而空速则是对载荷造成影响最主要的因素之一,飞机在平飞及下滑段载荷与空速的增加成正比增大,放襟爬升以及下滑段载荷因为空速差距较小因此基本持平,但是襟翼的偏度仍将在一定程度上影响飞机各部件的载荷分布。还可以看出,同一任务段下由于航线飞行质量大于训练飞行质量,前者机翼1g载荷大于后者。质量相同而装载不同时,航线飞行机翼载荷大于训练飞行,因为后者燃油多,无商载,而前者相反,且商载则分布于机身,燃油多分布于机翼,机翼燃油惯性力部分平衡了气动力,同时机身商载的存在要求机翼提供更大的气动力以承受飞机机身质量。基于此,处于航线飞行状态的飞机飞行情况下机翼受载程度更高。

图2 训练飞行1g各肋位弯矩Fig.2 The frame bending moment of training flight 1g condition
图3 航线飞行1g各肋位弯矩
Fig.3 The frame bending moment of airline flight 1g condition
训练飞行每g与航线飞行每g时机翼各肋弯矩增量的计算结果分别见图4和图5。构形不同是每g情况增量载荷的主要影响因素。对于襟翼偏度为0°的任务段,载荷大小基本持平。而对于襟翼偏角较大的任务段,每g载荷增量也较大。
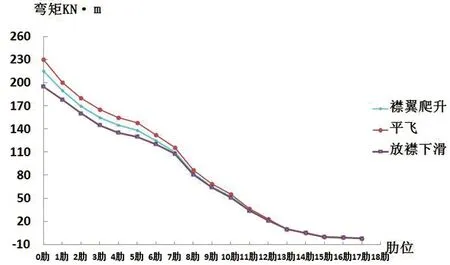
图4 训练飞行每g各肋位弯矩增量Fig.4 the frame bending moment increase of training flight each g condition
图5 航线飞行每g各肋位弯矩增量
Fig.5 the frame bending moment increase of airline flight each g condition
5 结 论
通过对某亚音速大展弦比飞机疲劳载荷计算结果的计算和对比分析,可以得出以下结论:
1)基于压力分布改进的二元升力线理论与风洞试验结合进行飞机各部件载荷计算的方法能够满足计算精度要求;
2)飞机不同任务段下飞行速度和外形变化分别是1g载荷和每g情况载荷大小的决定因素;
3)相同质量下机翼燃油惯性载荷的减载效果会导致大商载情况机翼受载较严重。

