柴油机曲轴静强度分析

李 宁,陈 克

(沈阳理工大学 汽车与交通学院,沈阳 110159)

大量试验表明,柴油机曲轴失效破坏的主要形式是弯曲疲劳断裂,这与曲轴的结构特点和受力工况有关。大多数研究采用整体曲轴进行分析,而曲轴静强度分析主要用于概念设计阶段对曲轴的评估,或用在优化设计曲轴时对比曲轴强度的变化,可不必采用整体曲轴模型[1]。

确定曲轴强度的方法有两种:一是试验研究、二是分析计算。由于试验研究费用高,只能在已制成的曲轴进行,不能在设计阶段进行,并且不能代表整批曲轴强度,因此应采用分析计算[2]。曲轴强度的计算方法主要有三种,即截断简支梁法、连续梁法和有限元法[3]。简支梁法计算简单,使用方便;连续梁法计算复杂,但与实测结果比较吻合;有限元法计算精确,可准确地计算出曲轴应力[4]。

本文基于有限元法加载余弦载荷,进行求解计算,得到应力分布情况,使用HyperMesh和Abaqus有限元软件联合对A和B两种不同几何结构的柴油机曲轴模型静强度进行分析。曲轴简化为1/2曲拐模型,采用不同网格类型对其划分,计算在余弦载荷工况下的曲轴强度,对于曲轴设计及优化具有参考意义。

1 曲轴模型的建立

根据柴油机曲轴结构参数,用Pro/E软件画出柴油机1/2 曲轴几何模型A、B,如图1所示。本文以A曲轴模型为例进行研究。特别注意在Pro/E中保存副本,格式为*.stp,以便导入HyperMesh。

图1 1/2曲轴几何模型

2 网格模型生成与处理

用Abaqus进行有限元分析计算之前,需要将网格进行处理。为在Abaqus中方便创建载荷,在主轴颈和连杆轴颈处建立一个120°对称约束接触面,再将单元类型更改为C3D10M。网格数目较少时,低高阶两种单元类型的计算精确度相差很大,此时采取低阶单元不合适。当网格数目较多时,低高阶两种单元的精确度相差不大,此时采用高阶单元不经济[5]。所以本文采用二阶四面体单元C3D10M,A曲轴网格模型如图2所示。

为在Abaqus中加载更为方便,在连杆轴颈上创建一个节点位移接触点集T,接触点集T的位置如图2所示。在主轴颈上加载径向弹簧约束(9个)。

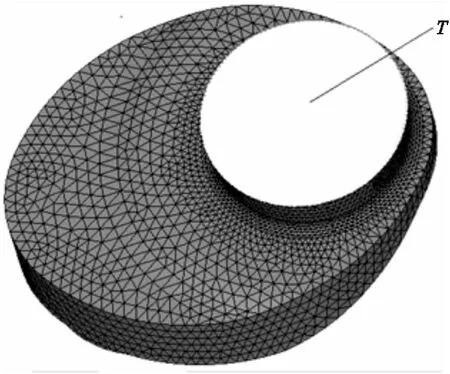
图2 网格模型

3 Abaqus有限元分析

Abaqus对曲轴进行有限元分析之前,要对模型先进行材料定义、建立接触关系和约束、建立分析步及加载等。然后提交运算,并对分析结果进行查看。

3.1 载荷计算

曲轴材料为45#钢,弹性模量206800MPa,泊松比0.30。表1为最大扭矩工况A、B型发动机最大爆压与转速。

表1 最大扭矩工况A、B型发动机最大爆压与转速

以A模型为例,采用1/2曲轴截断简支梁模型,曲柄销、主轴颈上径向施加120°余弦载荷,并采取轴向抛物线分布形式,模型示意图如图3a所示,两轴颈载荷分布示意图如图3b所示。曲轴强度计算参数见表2。

主轴颈载荷q1公式[6]

(1)

即

q1(X,Y,Z)=幅值×(1-4×Z×Z/28/28)×cos(1.5×atan(X/Y))

(2)

式中X、Y、Z代表坐标。

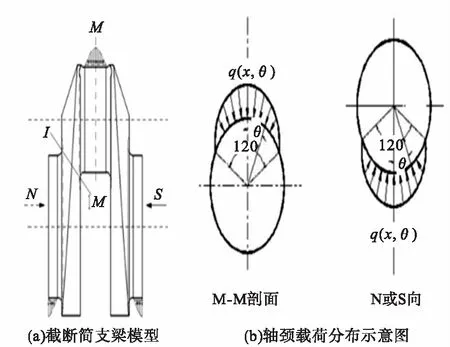
图3 截断简支梁模型和两轴颈载荷分布示意图

表2 A模型柴油机曲轴强度计算参数

连杆轴颈中心坐标的计算:连杆轴颈中心与主轴颈中心同在YZ平面内,所以连杆轴颈中心坐标在X方向的数值没有变化。Y方向距离为60mm。Z方向距离为

故连杆轴颈中心坐标为(0,-60,-64)。

连杆轴颈载荷q2公式[6]

(3)

沿用global(全局坐标系),将X、Y、Z分别用X、(Y+60)、(Z+64)表示,

即

q2(X,Y,Z)=幅值×(1-4×(Z+64)×(Z+64)/27/27)×cos(1.5×atanX/(Y+60))

(4)

上述式中的Fp表示曲柄销载荷,Fj表示两主轴颈支承反力,两者关系:Fj=Fp/2

最大受压状态下,曲柄销径向载荷为-131216.8N[7],左、右主轴颈支反力均为65608.41N;最大受拉状态下,曲柄销径向载荷为7327.42N[7],左、右主轴颈支反力均为-3663.71N。(正负号规则:拉正压负)。

3.2 加载载荷

Abaqus通过定义幅值加载余弦分布载荷,加载后的几何模型A如图4所示。

图4 加载余弦载荷后模型A

3.3 应力分布图

通过有限元计算可以得到A曲轴模型的应力结果。曲柄销圆角的应力以拉应力为主,所以取主应力的最大值来计算应力集中系数。主轴颈圆角的应力以压应力为主,所以取最小主应力的绝对值来计算应力集中系数。

图5曲柄销圆角处最大应力451.9MPa,图6主轴颈圆角处最大应力-443.7MPa。

有限元仿真优势在于比较准确得到曲轴最大扭转工况下的应力分布大小,清楚的看到曲轴的高应力区域,确定出高应力区域的最大应力值,为后面计算有效应力集中系数提供可靠依据。

图5 曲柄销应力云图

图6 主轴颈应力云图

4 曲轴强度计算

4.1 计算方案

计算方案:柴油机一个工作循环中,单拐曲柄销受到的最大载荷为最大爆压与惯性力的合力,最小载荷仅为惯性力;最大、最小载荷产生的交变载荷是引起曲轴破坏的主要因素。计算中将此两工况作为计算状态。

4.2 计算截面弯矩

单个曲拐的危险截面见图3中所示的1-1截面,该截面上所受应力易使曲轴发生断裂或失去负载能力,因此应计算出截面弯矩。最大受压状态的截面弯矩1771427.07N·mm,最大受拉状态的截面弯矩-98920.17N·mm。

4.3 名义弯曲应力

表3 名义弯曲应力 MPa

4.4 理论应力集中系数计算

有效应力集中系数kσ=1+q(α-1),式中q表示材料的敏感系数,对45#钢材料,取q0.4811[8]。则得到最大受压状态下曲柄销圆角处和主轴颈圆角处有效应力集中系数为2.58、2.55。

4.5 安全系数

曲柄销圆角和主轴颈圆角处,对钢曲轴的疲劳安全系数nσ、塑性安全系数ns的计算公式如下:

σm≥0时

(5)

(6)

σm<0时

(7)

(8)

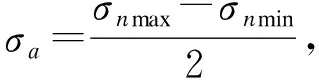
考虑到曲轴扭振的影响,安全系数n1、n2为

表4 材料参数选取表

表5 A曲轴模型各圆角处安全系数

针对不同的曲轴几何模型B,同样施加余弦载荷,按照上述同样的计算方法,计算出B曲轴最大扭矩工况下的安全系数,见表6所示。

表6 B曲轴模型各圆角处安全系数

钢曲轴许用安全系数取1.5。据表1可知,对A模型柴油机45#钢曲轴:最大爆压16MPa、最大转速1544rpm下,安全。对B模型柴油机45#钢曲轴:最大爆压13.5MPa、最大转速1400rpm下,安全。由表5、表6可知,A、B模型曲轴的安全系数皆高于许用安全系数,故A、B模型曲轴安全可靠。A模型曲轴的安全系数(n=1.78)比B模型曲轴(n=2.17)小,说明A曲轴设计在选取结构尺寸等方面还需进一步优化。

5 提高曲轴疲劳强度措施

柴油机曲轴的疲劳失效通常从应力集中处开始,因此在最大载荷不变的前提下,要提高曲轴的疲劳强度就应降低主轴颈和连杆轴颈过渡圆角处的应力集中效应。

(1)为改善两轴颈应力集中情况,可采用曲率变化的过渡圆弧曲线。在高应力区域选用较大的圆弧半径,这样可在一定程度上改善应力集中情况。

(2)采用加大圆角半径及圆角滚压强化的综合措施来提高曲轴的疲劳强度。增大圆角半径显然能降低圆角处应力集中,采用圆角沉割的方式滚压可使应力分散。

6 结论

(1)在轴颈圆角处有应力集中现象,曲柄销圆角处应力最大值比主轴颈处大,因此曲柄销过渡圆角处会因应力集中较易发生疲劳失效。

(2)采用两种曲轴模型进行疲劳强度分析,根据计算的安全系数得出两曲轴满足曲轴安全的要求,但A类型曲轴结构需进一步优化。

在计算分析的基础上提出了两种改善圆角应力集中以提高曲轴疲劳强度的措施,可以用于指导设计优化。