时差式超声波流量计改进方法研究

王玉琢，王洪源，陈慕羿，王连峻

(沈阳理工大学 信息科学与工程学院，沈阳110159)

流量测量是石油开发、日常供水、城市排水、农业生产等领域必不可少的一部分。从20世纪20年代起，国外科学家便开始了超声波流量计的研究，直至20世纪60年代末期，利用多普勒原理研制的超声波流量计才正式问世[1]。经过了近一个世纪的接力，流量计量技术不断更新，到二十世纪末期，随着科技的进步和工艺技术的发展以及高精度时间数字转换芯片TDC的出现，使超声波流量计的高精度测量达到了ps级。目前，国外主流的超声波流量产品流量量程可达0.01～25m/s，精确度可达0.5%[2]。相比之下，国产超声波流量计研究和发展较为滞后，目前市场上销售的AFV型超声波流量计精度小于1%，量程为0～30m/s；FV2000B33型超声波流量计，精度小于1%，量程可达0.01～32m/s。

与传统流量计不同，超声波流量计在安装方式、使用环境、功耗以及灵敏度方面都有极大优势，因此得到了广泛应用。超声波流量计虽已得到了普遍的认可，但其在工作过程中会受到温度、流体状态、超声波声速等的影响依然不可否认。因此，本文对其影响因素进行分析并提出切实可行的解决方案。

1 时差式超声波流量计传统流量测量原理

时差法流量测量理论是目前在流量计设计领域中应用最为广泛的一种理论，是通过利用时间差与流速之间的关系，求得流量的过程。由于多普勒效应，超声波在同一路径上顺流和逆流的传播速度是不同的，且与其传播时间成线性关系，所以可以根据这一关系，得到液体的流速。同时，管道的直径、长度等可以手动测量的参数都可视为已知条件，所以根据液体流量计算公式便可求得在某一段管道内某一时段的液体流量。图1 为时差法测量流速原理图[3-4]。

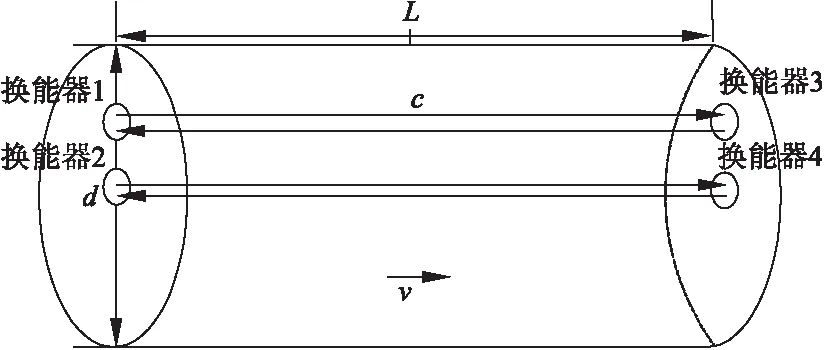
图1 时差法原理图

设管道直径为d，m；长度为L，m；液体流速为v，m/s；超声波静态传播速度为c，m/s。

当超声波顺流传播时，传播速度为静态超声波速度与液体流速之和，即c+v，则超声波顺流传播时间为

(1)

逆流传播时，传播速度为静态超声波速度与液体流速之差，即c-v，则超声波逆流传播时间为

(2)

超声波在液体中顺逆流传播时间差为

(3)

由于超声波在液体中的传播速度远大于液体的流速，即c2>>v2，将式(3)化简可得：

(4)

则，

(5)

根据流量定义可知，单位时间内流过的液体体积为流量。利用式(5)结合液体体积公式可得流量Q为(该式成立的前提条件是管道内的流体为单向均匀流动)

(6)

2 误差分析

不同流速的液体在流动过程中都会发生热交换，因此，温度对测量结果的影响不可忽略。同时，在实践过程中，发现影响流量测量结果的方面还有很多，但以温度、流速、以及管材为主。由于在本实验中对超声波探头进行插入式一字型摆放，所以下面主要对温度及流速两方面进行误差分析。

2.1 温度对测量结果的影响

常温下超声波在水中的传播速度为1500m/s，超声波在液体中传播时，随着温度的升高，超声波传播速度呈现先增大后减小的态势[5],且温度对超声波速度的影响是非线性的,如图2所示。

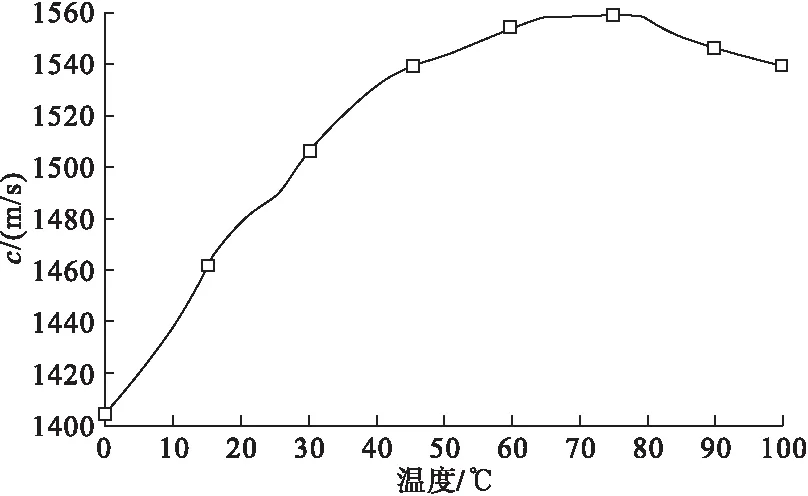
图2 超声波速度与温度关系图

当温度达到70～80℃时，超声波在液体中的传播速度达到峰值，此时与其在0℃时的传播速度差大于150m/s。根据式(5)可知，超声波速度对液体流速的测量结果至关重要，而由此带来的液体流量测量值变化将达到20%以上，因此必须进行温度补偿。

由于超声波声速的影响因素繁多，且获取指标困难，本文研究并实现了一种倒差式流速测量方法，其原理为：

根据式(1)可得：

(7)

根据式(2)可得：

(8)

将式(7)与式(8)做差运算，可得：

(9)

由此可得：

(10)

式(10)消除了超声波声速c对液体流速v的影响，从根本上保证了液体流速测量结果的稳定性及准确性。

2.2 流速对测量结果的影响

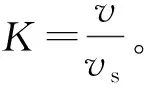
(11)

在流体力学中，流体在管道中流动时，一般分为三种状态，分别是：层流状态、湍流状态及过渡状态。流体状态不同，修正系数也会不同。而流体正处于何种状态，主要取决于雷诺数Re，其定义式为

(12)

式中：vm为流体管道横截面上的平均速度；d为管道直径；γ为流体的运动粘度。

当管径和流体运动粘度一定时，层流态转化为湍流态时的速度称为上临界速度；反之，称为下临界速度。当管径和流体运动粘度改变时，临界速度也随之改变，但是，无论发生何种变化，Re不变，并且，上临界雷诺数Rec为2320，下临界雷诺数Rec’为13800。当Re>Rec’时，管道中的流体为湍流状态；当Re2320时，管道中的流体为湍流状态。

2.2.1 层流状态修正系数

当流体处于层流状态时，其在管道内呈抛物线分布，处于管道中轴线上流动的部分速度最大为vmax。以管道直径为沿线的流速为

(13)

式中，vr为r处的流速；r为直径方向的径向距离。

通过对式(3)积分可得其线平均流速和面平均流速分别为：

(14)

(15)

由上两式可得层流状态下的流速补偿系数为

2.2.2 湍流状态修正系数

当流体处于湍流状态时，流体在管道内径向流速差异小于层流状态。仍然是位于管道轴线处的流速最大。处于湍流状态时，其运动方程求解过程复杂，因此，通常管道湍流状态的速度分布用经验性指数公式表示如下：

(16)

式中n为管道雷诺数与管道粗糙度的函数。

通过对式(16)积分可得其线平均流速与面平均流速分别为：

(17)

(18)

综合上两式可得，湍流状态下的系数补偿为

当流体处于过渡状态时，采用经验公式[6]计算K值大小：

K=1.119-0.011logRe

3 计时模块对测量结果的影响

由本文研究的倒差式流量测量理论可知，超声波传播时间的测量对流量计算结果具有决定性影响，时间测量模块的精确度将直接影响流量的测量结果，因此，采用TDC-GP22高精度计时器，可以一定程度上确保流量测量的精确度。

TDC-GP22是德国ACAM公司生产的一款基于CMOS设计的，根据内部逻辑门的延迟来进行时间间隔测量的一款计时芯片，是GP21的升级产品，TDC-GP22芯片最主要的提升是内部集成了一个第一波识别模式，更好的适用于高动态范围的应用。其测量范围为500ns至4ms，单通道典型分辨率为90ps，四精度(双传感器)模式最高分辨率可达22ps[7]。其内部具有两种测量范围(测量范围1和测量范围2)，验证过程采用的是测量范围2。

测量范围2中，只有一个stop通道对应start通道，并且具有3次采样能力，可以自动进行计算并自动校准。每个单独的stop信号都有一个精度为10ns的可调窗口，可提供准确的stop使能。其测量原理如图3所示。

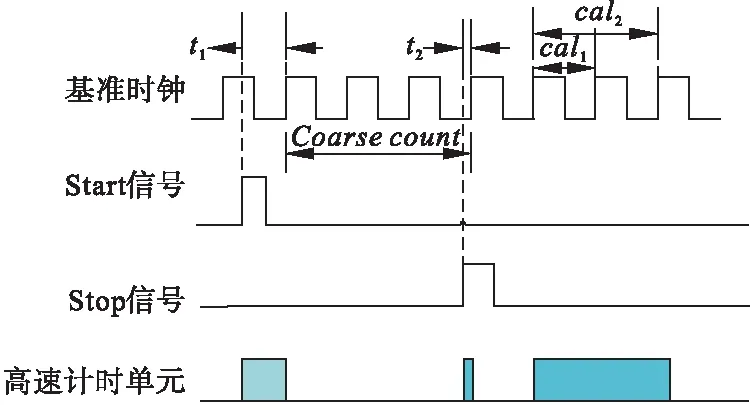
图3 TDC测量范围2工作原理图

由图3可知，TDC高速单元只是测量start/stop信号到相邻的第一个基准时钟上升沿间的时间间隔，即t1/t2(该部分为精确计数)，而非整个时间间隔。并且TDC会记录下两次测量所经历的基准时钟周期数，即coarse count(该部分为粗值计数)[8]。在测量范围2，将寄存器3的第31位EN_AUTOCALC_MB2置为1，TDC会自动计算所有开启获得的脉冲，并将这些结果写入寄存器4中。由于测量范围2的特殊测量方法，Start脉冲在TDC内部作为Stop脉冲处理。

ALU计算的时间间隔如下：

Time=RES_X*Tref*2CLKHSDIV

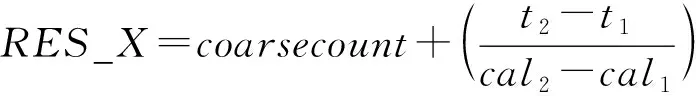
若实验管道长度为15cm，以液体中静态超声波速度为1500m/s，液体流速为0.2m/s进行测试，可得时差Δt约为27ns。根据前文所述，单通道典型分辨率为90ps可知，理论上所得测量误差将小于0.4%。

4 硬件设计

硬件实现部分是采用TDC-GP22与Arduino相结合的方式。在TDC-GP22外围电路中，添加一个4MHz外部晶振，作为TDC-GP22的高速校准时钟单元；用一个32.768KHz的晶振作为基本时钟单元，并从此发出start或stop脉冲，图4为TDC-GP22芯片电路图。

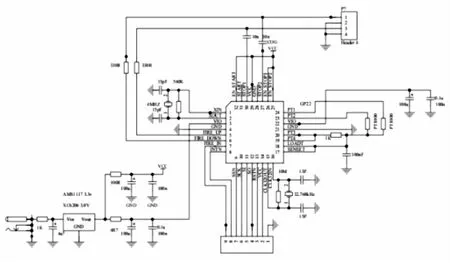
图4 TDC-GP22内部电路图

Arduino Uno控制板的核心处理器为ATmega328，接口丰富，便于同时控制TDC-GP22以及其他功能模块。但相较于Arduino内部的计数器，TDC-GP22测量时间差/频差的精度更高。同时，利用TDC-GP22的第一波检测功能，还可以有效降低管道内气泡等杂质对测量结果造成的影响。

Arduino控制板通过SPI总线与TDC-GP22相连接，Arduino向TDC-GP22发送指令，再由TDC-GP22内部的脉冲发生器向超声波传感器发射脉冲信号，经过片内时间窗延迟后产生启动信号，在回波信号处理电路中产生停止信号。回程相同，Arduino从TDC中读取数据。通过TDC内部的ALU计算出往返的时间差，并确定出管道中流体的顺逆流传播时间，从而计算出流量。

5 实验测试

测试环节主要完成两个实验：流速补偿实验和理论验证实验。图5为主要部件实物图。图6为实验装备结构示意图。

图5 主要部件实物图

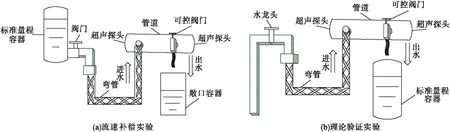
图6 实验装备结构示意图

5.1 流速补偿实验

将两个相同流量计在同一温度下(室温)安装至被测管道装置测量位，并对其中一个流量计进行流速补偿。将阀门开至不同程度以控制流速及流量，对大、中、小三种不同流量类型，分别以3.6s为测量时间进行流量测量，并将测量结果进行对比。实验结果如表1所示。

由表1中的数据可知，未进行流速补偿的流量计，测量流量越小结果误差越大；进行流速误差补偿的流量计测量结果的误差相对稳定。在实验中，未进行流速补偿时，误差最大为7.8%，最小为2.7%，相差4.9%；进行流速补偿后，误差最大0.9%，最小0.4%，相差0.5%。

5.2 理论验证实验

将时差式流量计和倒差式流量计均进行流速补偿并在同一温度下安装至流量测量位。将阀门位置固定，以相同的流速使容积为3L的容器在出水口接水至盛满容器。改变水温，分别在25℃、50℃、75℃做上述实验，对两个流量计进行测试，每个温度实验三组。测量结果如表2所示。

由表2数据可知，时差法流量计在不同流体温度下的流量测量结果稳定性较差，温度越高测量结果误差越大；倒差式流量计对于不同温度下的流量测量结果误差相对较小，不同温度下的流量测量结果相对稳定。在实验中，时差法流量计在不同温度下，最大误差为-1.52%，最小误差为0.39%，相差1.91%；倒差式流量计在不同温度下最大误差为0.91%，最小误差为0.32%，相差0.59%。

5.3 实验结果分析

由于在改进的倒差式测量原理中，消除了温度对流速测量结果的显著影响，因此降低了流量测量的复杂性和不确定性，提高了测量的准确度。TDC-GP22第一波检测功能的应用很好的解决了气泡干扰问题，便于有用信号的提取。结合实验数据可知，采用倒差式流量测量理论并用流速补偿标定后的流量计能很好的适应各种液体温度下的不同流量类型，测量结果稳定性和准确性相较于时差式测量理论及未进行流速补偿的流量计都有明显提高。

6 结论

通过理论分析对流量测量原理进行改进，结合误差分析对测量结果进行误差补偿，并通过实验验证了改进原理及误差补偿方法的可行性和准确性。实验数据证明，对影响因子进行改进后的流量计，有效减小了测量误差，提高了测量的稳定性。