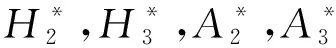宽体式扁平钢箱梁颤振特性分析

张亮亮，游志雄，符 健

(1.重庆大学 土木工程学院，重庆 400045；2.中国市政工程中南设计研究总院有限公司 第四设计院，湖北 武汉 430019)

随着大跨度桥梁不断涌现，轻质、轻柔成为桥梁结构的发展方向，桥梁的宽高比随之不断增大，扁平式钢箱梁因而广泛地应用于大跨斜拉桥和悬索桥中。但随着宽高比的增大，桥梁对风的作用越来越敏感，桥梁由于颤振形成的气动力而出现失稳现象，最终导致破坏，因此有必要对宽体扁平钢箱梁颤振特性进行研究。

众多学者对大跨度桥梁结构的颤振特性进行了研究。辛大波等[1]通过分析不同雨强下主梁的颤振临界风速以及颤振导数，得到大跨桥梁颤振稳定性受降雨的影响规律。熊龙等[2]在考虑静风效应的基础上，采用状态空间法对大跨度桥梁进行了三维颤振分析。李翠娟等[3]提出大跨悬索桥的扭转刚度可以通过设置交叉吊索得到显著的提升，提高大跨悬索桥的颤振性能。白桦等[4]给出了以三分力系数为基础并可快速评价桥梁颤振稳定性的参数F，利用参数F可快速将不同方案的颤振稳定性进行分析对比,便于气动选型。陶仕博等[5]在萤火虫算法的基础上，使其同量子遗传算法中的量子计算、变异和交叉操作相结合，得到混合萤火虫算法，并用于对桥梁颤振进行分析。夏锦林等[6]结合了二维3自由度的颤振分析方法，研究上下组合的中央稳定板对跨海悬索桥箱梁颤振特性的影响。许福友等[7-8]提出了改进的随机搜索算法和新颖的直接方法确定桥梁的18个颤振导数。PHAN等[9]通过二维桥面模型试验指出机械控制可以提高悬吊桥颤振速度。VU等[10]提出利用复杂记法计算桥梁断面18个颤振导数的精确公式。PATRUNO等[11-12]发现RANS模型在预测颤振初始速度方面非常准确。SARKIC等[13]发现采用URANS方法可以高效地导出桥梁颤振导数。上述文献对跨度较大桥梁颤振特性的影响因素与其颤振稳定性评价方法进行了研究，但针对宽高比相对较大的扁平钢箱梁颤振特性开展的研究较少，采用数值模拟与风洞试验相结合对宽高比相对较大的扁平钢箱梁颤振导数识别与临界风速求解的文献也不多。

本文采用数值模拟与风洞试验相结合的方法研究宽高比为12的宽体式扁平钢箱梁的颤振特性，求解其在成桥状态与施工状态的颤振临界风速值，并识别扁平钢箱梁在3种不同透风率下的颤振导数。

1 工程概况及模型设计

1.1 工程概况

寸滩长江大桥为双塔单跨悬索桥，全长 1 600 m，其主桥跨径布置为(250+880+250)m，矢跨比为1/8.8。加劲梁的宽高比为12，梁高为3.5 m，梁宽为38 m。桥位场地类别为B类，桥面设计标高为267.8 m。主梁的标准横断面见图1。

图1 主梁标准横断面(单位：cm)

1.2 模型设计

采用木材制作主梁节段模型，用塑料板制作其他附属结构。节段模型的几何缩尺比定为1/60，模型的长度、宽度、高度分别为2.1，0.7，0.058 m。主梁节段模型风洞试验考虑成桥和施工2种不同状态，模型具体的设计参数见表1、表2。

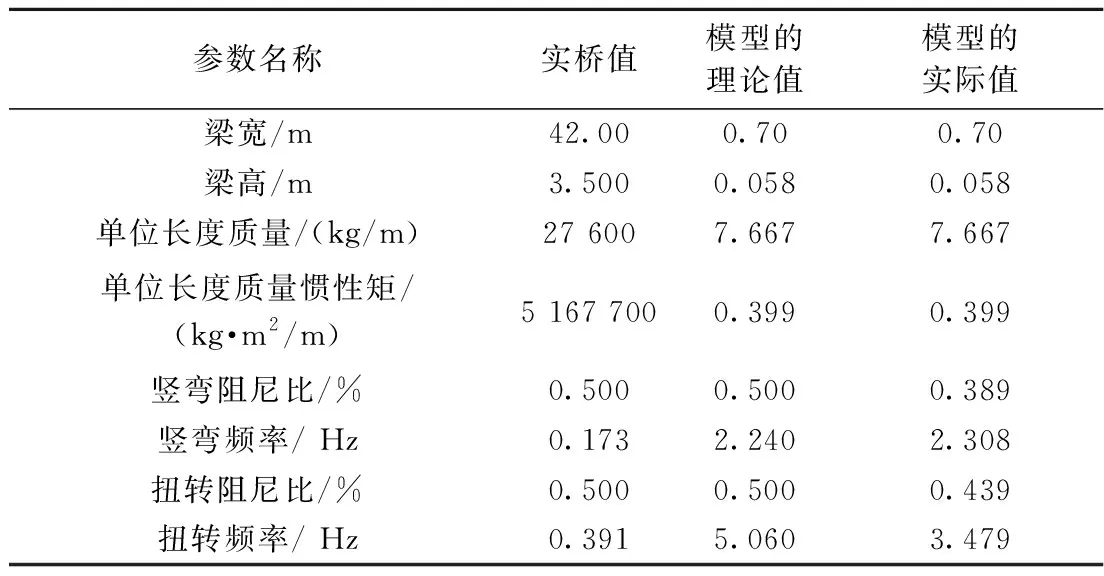
表1 成桥状态节段模型参数

表2 施工状态节段模型参数

为模拟主梁在扭转和竖向2个自由度上的振动特性，用8根拉伸弹簧把已制好的动力节段模型挂在支架上，弹簧间距为108.0 cm，使之形成2自由度振动系统。试验在节段模型下部一定高度处固定2个激光位移传感器，位移传感器间距为40.0 cm，并且将其对称放置在模型中心线两侧，以测试桥面边缘处位移响应。动力节段试验模型见图2。

图2 风洞中的动力节段试验模型

本节段模型试验主要在不同工况下测定主梁临界风速及在均匀流下识别不同风速(4～18 m/s，间隔 2 m/s)的颤振导数。

1.3 数值模拟

为验证数值计算程序的可行性，将平板数值计算结果与Theodorsen理论解进行对比。模拟平板横截面尺寸见图3。对比结果见图4。图中各符号的含义见后文2.1节。

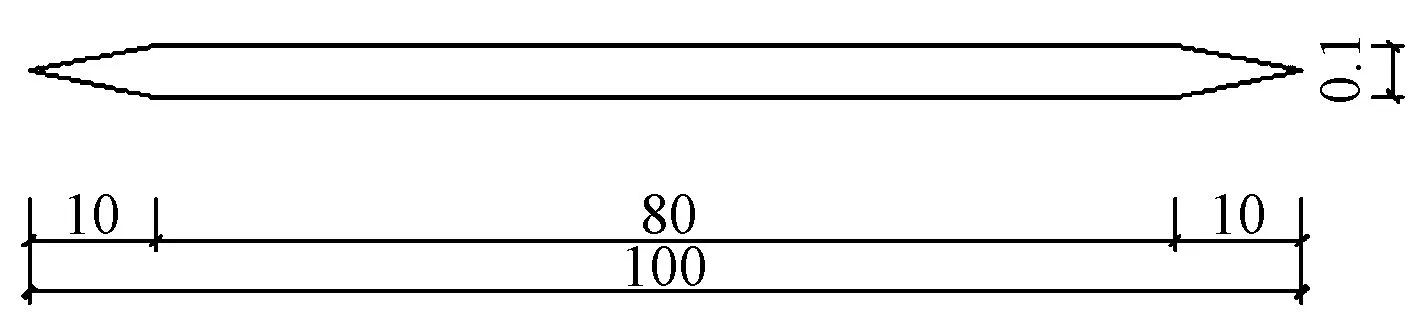
图3 模拟平板横截面尺寸(单位：cm)

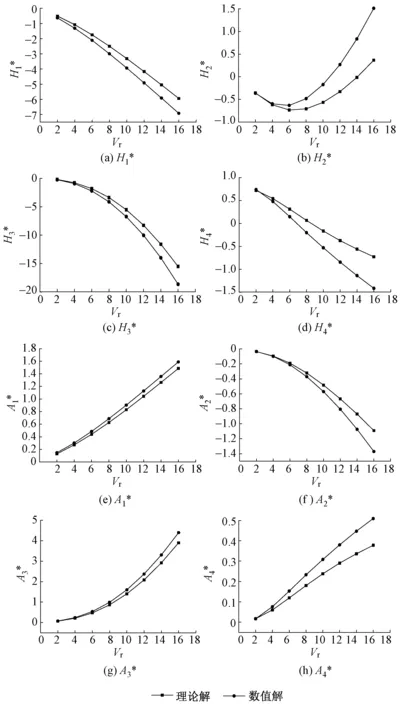
图4 平板数值模拟结果与Theodorsen理论解对比

由图4可见，在折算风速比较小时，数值解与理论解很接近，之后随着折算风速的增加，两者的偏差也随之增大。但通常在验算颤振稳定性时，针对其相应的颤振检验风速，仅需要在较小折算风速范围内的相应颤振导数，因此折算风速较大时所存在的偏差对结构的颤振稳定性验算影响较小。另外，平板的数值解与理论解随折算风速的变化趋势明显一致，说明了数值模拟识别颤振导数的可行性。

在数值模拟中,主梁节段模型几何缩尺比的大小仍设置为1/60。流场网格划分为刚性边界层网格区域、动网格区域、静止网格区域3个部分[14]。用GAMBIT软件划分刚性边界层网格、动网格、静止网格，网格数分别为 36 437，72 195，27 096，具体见图5。采用FLUENT软件对其分析，基本参数见表3。

图6 节段模型颤振导数风洞试验结果与数值模拟计算结果对比(施工状态)

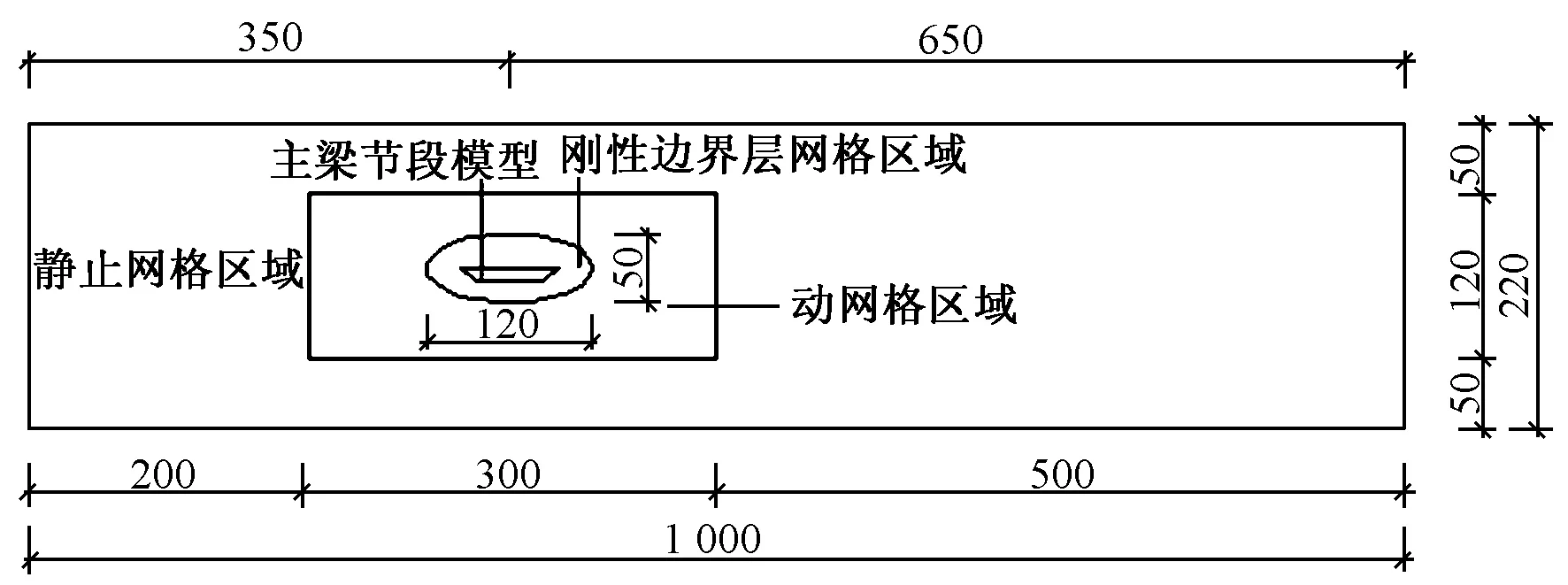
图5 数值模拟流场的区域设置(单位：cm)

表3 FLUENT软件的基本参数

计算采用k-ε标准湍流模型，湍流黏性比为10，取进出口湍流强度为5%；不考虑能量交换和温度变化；取入口风速分别为4，8，12，16，20，24，28，32 m/s；时间步长取为0.01 s。

2 数值模拟结果与风洞试验结果对比

2.1 颤振导数对比

对比施工状态下节段模型对应的风洞试验结果和数值模拟结果，见图6。

采用主梁节段模型风洞试验和数值模拟方法研究颤振导数。改变栏杆的透风率，将主梁节段模型的颤振导数相关研究分为3种情况，见图7。

图7 主梁的3种透风率栏杆(单位：m)

由图7可见，人行道栏杆透风率从大至小依次为59.8%，45.8%，35.6%。在3种透风率下，主梁节段模型颤振导数的风洞试验结果与数值模拟计算结果对比见图8。

图8 主梁节段模型颤振导数风洞试验结果与数值模拟计算结果对比

由图8可知：

1)风洞试验中所设置的3种不同透风率栏杆，对主梁模型8个颤振导数在总体变化趋势上基本没有影响，仅是数值大小有所差别。

2)风洞试验中，在折算风速比较小时，主梁模型(设置3种不同透风率栏杆)的颤振导数大小比较接近，而随着折算风速的逐渐变大，颤振导数大小差异明显变大。这表明折算风速对不同透风率栏杆的颤振导数值影响较大。

2.2 颤振临界风速对比

根据文献[16]规定，成桥状态下桥面高度处的设计基准风速为

Vd=V10(Z/10)α=27.5×(122.8/10)0.16

=41.08 m/s

(3)

式中：Vd为设计基准风速；V10为桥址处设计风速，为标准高度10 m、平均时距10 min、重现期100年的平均年最大风速；Z为构件基准高度；α为地面粗糙度系数，根据文献[16]表3.2.2取值。

施工阶段的设计风速为

Vsd=ηVd=0.92×41.08=37.79 m/s

(4)

式中：Vsd为不同重现期下的设计风速；η为风速重现期系数，根据文献[16]表3.3.1取值。

因此，成桥状态的颤振检验风速为

[Vcr]=1.2μfVd=1.2×1.256×

41.08=61.92 m/s

(5)

式中：μf根据规范[16]表6.3.8取值。

施工阶段的颤振检验风速为

[Vcr]=1.2μfVsd=1.2×1.256×

37.79=56.96 m/s

(6)

主梁节段模型在风洞试验中可通过直接测量获得临界风速值的大小；而其数值模拟下的颤振临界风速大小通过SCANLAN二维颤振临界风速计算方法求得。结果对比见表4。

表4 数值模拟与风洞试验的颤振临界风速对比 m/s

对比2种方法下的颤振临界风速值，结果较为接近，而且不同方法下的结果均比颤振检验风速值要大，这表明寸滩长江大桥的颤振稳定性满足要求。桥梁的颤振临界风速可通过数值模拟计算的方法进行预估，在桥梁的初步设计时可以运用该计算结果，具有一定的工程意义。此外，对比2种不同状态下的颤振临界风速值，成桥状态下的数值相对要小，表明主梁上的附属结构对主梁的颤振稳定性产生不利作用，因此在设计时应慎重设置附属结构。

3 结论

1)成桥状态下的颤振临界风速值相比于施工状态下的颤振临界风速值要有所减小，表明主梁上的附属结构会对主梁的颤振稳定性产生不利作用，因此在设计时应慎重设置附属结构。

2)成桥状态下，主梁模型(设置不同透风率栏杆情况下)的8个颤振导数在整体变化趋势上基本没有影响，仅数值的大小存在差异。折算风速比较小时，主梁模型(设置不同透风率栏杆)的颤振导数大小比较接近，而随着折算风速的逐渐变大，颤振导数大小差异不断地变大。这表明折算风速对不同透风率栏杆的颤振导数值影响较大。