基于智能算法的防空阵地标定流程优化研究∗
谢瑞煜 高绍忠 孙 瑾
(1.海军航空大学 烟台 264001)(2.中国人民解放军91697部队 青岛 266400)
1 引言
现代战争的一大特点就是:空地结合,越点打击。实现这一战术的基本途径就是通过强大的空中力量,包括作战飞机、巡航导弹和精确制导炸弹,高密度地实施对地面攻击,从而达到和实现摧毁地面有生力量的战术目的。现代战争战术的演变,也要求新一代防空导弹武器装备具备新的、先进的战术技术性能[1]。
防空武器系统在阵地部署时,必须先进行标定。按照战术技术的要求,防空武器系统在作战状态时,必须纳入全国防空情报网,武器系统应具备定向定位的手段[2]。它是通过地面作战系统中的指挥单元来实现的。同时由于地面作战系统的各设备在阵地上是分散布置的[3]。为完成各车间的目标坐标的传输、变换和修正等,作战装备间应进行方位和距离的标定。即确定各车之间的相对距离和相对方位角度[4]。
比如某型防空武器系统的标定包括指挥单元(A)的绝对标定及指挥单元、火力控制单元(B)和武器单元(C)之间的相对标定。
2 标定流程优化问题
2.1 标定流程
防空阵地展开完成后,各车辆之间开始进行标定,标定过程中首先对B车进行绝对标定,其采用的方法是通过车载数字罗盘进行寻北,测量车辆机械零位与正北方向的夹角,这项步骤是设定该防空武器系统以正北为基准,方便系统与友邻系统有一个更好的对接。
对A车完成绝对标定之后,就开始着手A车与B车,B车与C车的相对标定,这项标定流程也是本文考虑的重点流程。相对标定采用光学互瞄方式,即方位角通过标定望远镜互瞄雷达上的十字确定,距离则由激光测距仪进行测距[5~6]。
2.2 标定流程优化的数学模型
标定流程优化问题,是在一定的优化目标和约束条件下,解决要求的在多辆车同时标定时的最短时间问题。在S车进行绝对标定后,相对标定要按照一定的规则进行。在进行B车标定时,B车不能同时与两辆车及以上进行标定。在进行C车标定时,只需要与对应B车进行相对标定,因为C车在进行发射时,发射指令由对应的B车发出,它的标定只需要与B车进行相对标定即可,不需要再与A车进行相对标定;同时其标定的参数涉及到方位角和相对距离,方位角的标定需要首先知道B车机械零位与正北方向的夹角,因此,必须先将B车与S车进行相对标定,才能进行与C车的标定。基于考虑上述因素,本文给车辆标定流程优化的数学模型。
假设阵地上有1辆指挥单元A,火力控制单元为 Bi,i=1,2,…,m ,武 器 单 元 为 Cj,j=1,2,…,n。S车与每辆B车要进行标定,记A车与Bi车的标定时间为ti,C车与对应的B车进行标定,记Cj车与Bi车的标定时间为Ti。
标定流程在约束条件下,总的时间要求最短,即目标函数可表示为

约束条件:
(a)B车与C车的标定必须在同一辆B车与S车标定之后才能进行;

(b)B车与A车,B车与C车的标定只需一次。
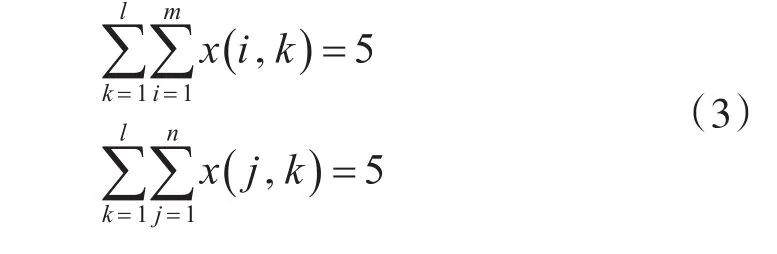
3 求解算法
针对上一节给定的标定流程优化问题的求解,本文采用两种智能优化算法——粒子群算法(PSO)和遗传算法(GA),PAO作为一种典型的智能优化算法,虽然在计算上和GA有着很多相同的地方,但是遗传算法的因子是用生物技术中的杂交和变异时计算所要的,而粒子群算法在搜索时是模仿鸟、兽、鱼等动物群体来实现的,因此粒子群算法有着许多优点,比如有一定的并行性,实现简单,控制参数不多,概念容易理解。但是粒子群算法在有着众多优点的同时,也在许多方面存在需要进一步研究的内容,尤其在理论分析和应用研究领域需要得到更多发展。PSO有着算法跳出局部最优解的能力不足,算法求解高维复杂多峰问题的精度不高、算法的计算复杂度过高,针对单目标优化问题时,不具备处理约束条件和多目标的机制等缺点。为了求解本文含有约束条件的离散标定流程优化问题,本文采用基于离散二元粒子群算法DBPSO(Discrete Binary Particle Swarm Optimization)对该优化问题进行求解[7~8]。
3.1 离散二元粒子群优化算法简介
3.1.1 标准粒子群算法
设种群的大小N,每个粒子在t迭代时刻的D维坐标空间上的位置:同时粒子的速度:在t+1时刻,粒子位置xi(t)和速度vi(t),可以用下面的公式进行变换:

粒子在探索和开发时寻找最优的位置,粒子群算法的运行快慢将因为这两种寻找方式而受到许多影响。原始PSO如果引入惯性权重,将会使这两种搜索得到更佳的控制,它的速度更新公式如下:

公式中,Tmax表示最大进化代数;Wmin表示最小惯性权重;Wmax表示最大惯性权重;t表示当前迭代次数。在大多数的应用中Wmax=0.9,Wmin=0.4[9]。
3.1.2 DBPSO算法
20世纪末,Kennedy和Eberhart提出了在编码方式上与PSO有所不同的基于PSO算法的离散版粒子群算法BPSO,这个改进算法同样要考虑粒子的数目,粒子的长度,粒子的范围,粒子的速度,学习因子,关行权重等等几个变量,有所不同的是标准粒子群算法的粒子位置,速度都是实数域内是连续编码的,但是BPSO中的例子位置使用0,1二进制表示,从而我们也将其称为二进制粒子群算法或二元粒子群算法。
二元粒子群算法的在数学表达上与标准粒子群算法不同是用一个函数——sigmoid函数来实现的:

其数学表达式为

3.2 采用DBPSO算法的标定流程
标定流程问题的候选解 x(i,k),x(j,k),i=1,2,…,m ,j=1,2,…,n,k=1,2,…,l,是两个粒子,所以粒子的维数为m×l或n×l。文涉及到约束条件,可以采用罚函数法来进行处理,通过罚函数法,将标定流程的优化问题转化为一个无约束目标的优化问题,最后经DBPSO算法或者GA算法进行解算。
针对约束条件[10],定义的一个罚函数 f2,为了使结果中的违反约束条件的解与正常解有较大区别,这里设定一个惩罚系数k,本文取k=100。则f2可表示为

式(9)中VI为不满足约束条件(a),(b)的个数。
最后,可得到如式的无约束优化问题:

式(10)中 f0是DBPSO算法或GA算法的适应函数[11]。
3.3 DBPSO算法流程
1)建立阵地车辆相对标定的数学模型,确立目标函数,约束条件,利用罚函数法将有约束条件的优化问题转化为无约束条件的优化问题,得到DBPSO的适应函数。
2)定义DBPSO,初始化粒子群的种群数量,粒子的维数,限定粒子群的位置,制定速度的范围;设定迭代的总次数。
3)获取A车与B车,B车与C车之间的相对标定时间这几个基本参数。
4)将数据代入DBPSO的适应函数得到第一个适应度值,将各个粒子的位置作为它们的个体最优值(pbest),并从中选取群体最优值(gbest)。
(5)根据DBPSO的更新公式,更新粒子的位置、速度,并计算适应值。
(6)迭代结束后,在所有的 pbest中选取gbest,并将这个全局最优值作为最终的优化结果输出[12]。
4 算例分析
假设一个防空阵地上需要标定的车辆是一辆A车,5辆B车,5辆C车,它们相对标定的时间如表1所示。

表1 车辆相对标定的时间
表1中A—GPi表示A车与B车的相对标定,Cj—Bi表示C车与B车的相对标定
本文采用的DBPSO算法例子种群群数为50,迭代次数为200;GA算法种群数为50,迭代次数为200,交叉率为0.7,变异概率为0.01。结果如表所示。

表2 DBPSO算法和GA算法的最优解
表1中采用DBPSO算法和GA算法的适应值相等,说明两者的收敛情况一样,通过在多次仿真试验后,发现这就是最优解,最优的标定时间即为11.5min。

表3 基于DBPSO算法和GA算法的最优流程
表2是分别用DBPSO算法和GA算法而到的具体标定流程,而且两者的最优流程一样。
图1只截取了迭代前60次的收敛图,图上DBPSO算法在收敛性上明显比GA算法快,而且两者最后都能收敛到全局最优[13]。

图1 DBPSO算法和GA算法的收敛曲线比较
5 结语
本文针对防空阵地车辆标定流程中的不足,提出了一种基于智能算法的标定流程优化方法,建立了使标定时间最小化的数学模型,通过罚函数法,将有约束条件的问题转化为无约束条件的问题。同时针对普通粒子群优化算法的不足,将其进行改进,在保持粒子群算法传统的解算速度快这项优势情况下,要求提高其寻找全局最优解的能力。结果通过与遗传算法的仿真实例对比,发现,DBPSO不仅解算速度快,而且容易寻找到全局最优解,在标定流程的优化问题中能得到良好的应用。
通过智能算法的优化,标定的流程得到改善,时间得到最大限度的缩短。在现代战争的背景下,时间对战争胜负产生巨大的影响,标定时间的缩短,意味着防空阵地的展开部署效率大大提升,给后续的目标搜索、指示、跟踪、制导留下大量时间,有效提高目标的拦截的概率。

