基于排队论的防空系统射击效率模型研究∗

宋 剑

（海军陆战队训练基地 广州 510430）

1 引言

空中威胁复杂多变，手段呈多样化、综合化、一体化和系统化。当有空中目标来袭时，如何分配防空武器是极为关键。是使用一种武器组成多道防线防空系统，还是同时使用多种武器同时组成多防线防空系统？这些都需要指挥员进行决策，要决策出来哪种防空效果更好。研究地面防空系统作战效能、地面防空作战部署方案优化和地面防空作战资源需求等问题时，如何决策都必然涉及地面防空系统射击效率问题，排队理论是人们通常选择的用于计算射击概率的方法，它的射击过程类似于排队论的服务系统与顾客的关系，防空效能也可以应用排队论进行计算［1～2］。

防空过程中，防空系统就是“服务机构”，来袭的空中目标是“顾客”，当来袭目标超过超出服务能力后，顾客来袭目标肯定不会等待，就叫做放弃服务，因此就突破防御攻击成功了。因此，应用排队论的方法，建立了M/M/C/C排队模型，为解决单层防空系统、同类或不同类武器组成的多道防线防空系统效能的计算问题提供了一个有效的途径，进而决策出哪种设计方案效能最高［3～4］。

2 防空系统射击效率模型指标

2.1 目标流

现代空袭兵器的速度越来越快，来袭目标一般具有排队论所谓的顾客流的性质，称为目标流。来袭目标流具有不同程度的泊松特性，我们建立数学模型时把目标流处理成最简单流。但这种假设对于实际只能是一种近似，服从分布的参数记为λ，其物理意义为单位时间来到的目标的平均数，它表明了目标流的强度［5～6］。

2.2 服务

来袭目标受到侦测；其信息为情报中心录取和处理；目标受到一次攻击。

2.3 服务台

侦察、测量系统，指挥系统的信息处理中心，一门高炮（或高炮连）或导弹发射架。

2.4 服务时间

理论上、实践上一般都把射击时间看作服从指数分布的随机变量，有时采用k级爱尔朗分布的假设。在服务时间为指数分布的假设下，参数μ是单位时间所射击的目标的平均数，1/μ是射击一个目标平均所需时间。

2.5 排队规则

防空系统一般是损失制排队系统。当防御武器不足以应付所有来袭目标时，多出来的来袭目标就会飞过这种武器的防御区，这就是所谓的“顾客离去”。

一般情况下，射击武器（服务台）都采取“先来先服务”的规则。但在多目标情况下，防空系统选择对我威胁最大的目标优先射击（实行优先权服务）。

2.6 系统的稳态特性

从数学上看，系统的稳态要经过无穷大的时间才发生，但实际系统只要求时间足够长久可认为是稳定的。有研究表明，在防空系统中，如果空袭时间超过一部武器对目标的作战时间的2～3倍，就稳定了。也就是说射击过程的非平稳性实际上对系统的统计特性已影响甚微，可以应用所获得的各个稳态公式［7］。

2.7 火力配置与防空系统的效能［8～9］

体现射击效果，主要数量指标有：

防空系统能够击落空中目标数的数学期望或对来袭目标的毁伤概率；

能够突破防空系统的目标数的数学期望值或来袭目标的突防概率；

从提高防空效率的可能性出发，对防空武器的主要战术技术性能作出评价；

根据要达到的防空效率，在给定防空武器的战术技术性能的条件下，确定防空系统的组成与配置。

各个数量指标都可以直接或间接地用来改进射击的效果。在对目标射击的计算中，不考虑目标的还记。这绝不仅仅是为了数学处理的方便，而主要是由从现代防空作战的特点出发，按不给敌人还击时间的要求，以目标进行火力对抗之前开始射击的战术原则为前提进行火力系统的效能估计，故可以不考虑目标的还击。

3 单层防空系统的模型

假设空袭目标流可看作最简单流，强度为λ；记来袭目标总数为N。守方为单层防线的防空火力系统，共有C部同类型防空武器。各武器的射击时间服从参数为μ的指数分布；每一架飞机（或每一枚导弹）只受一座防空武器射击，被击毁概率为P；如果目标飞临时因C部防空武器都无暇射击或虽该目标遭受射击但未被击毁，则该目标突防［10］。

使用爱尔朗公式可算：

状态分为三类：

1）所有武器都不射击，概率为：

2）C座武器中有n座射击，n=1，2，…，C-1 ，概率为：

3）所有武器都正在射击，概率为：

此外，目标受到射击的概率Ps，即防空武器有“空闲”的概率

目标被击毁的概率为：PH=Ps⋅P=(1-Pc)P。

目标突防概率为：Pt=1-PH=1-(1-Pc)P。

被击毁目标的数学期望为：MH=N ⋅PH=N ⋅(1-Pc)P 。

突防目标的数学期望为：Mt=N ⋅Pt=N ⋅[1-(1-Pc)]P 。

正在射击的武器数的数学期望为：

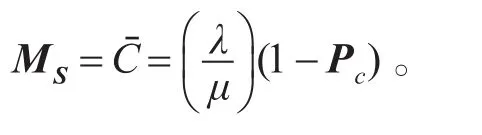
4 由同类武器组成的多道防线防空系统

假设由同类武器组成α道防线，每道防线上配置 C1，C2，...，Cn个火力单位。

在第一道防线上得不到射击而突防的概率为

当第一道、第二道防线上的所有火力单位都在射击时，后到的敌机才得不到射击而突破防线。因此，敌机突破第二道防线的概率为

以此类推，敌机得不到射击而突破α道防线的概率为

5 由不同类武器组成的多道防线防空系统［11～12］

1）目标流为泊松流/强度为λ；

2）来袭敌机通过各防线只受到一类武器的射击。目标在各防线停留时间较短，以致不能保证各防线完全可靠地毁歼目标；

3）设各道防线上的武器对目标射击时间都是随机变量，它们分别为 μ1，μ2，...参数的负指数分布。

任意时刻，该防空系统在抗击目标流时的可能状态为：

S00第一、第二道防线都不射击；

S10第一道防线正在射击，第二道防线不射击；

S01第一道防线不射击，第二道防线正在射击；

S11第一、第二道防线都在射击。

则系统稳态概率的代数方程组如下：

得到下列稳态解：

1）两道防线上武器都不射击的概率：

2）第一系统忙，第二系统空闲的概率：

3）第二系统忙，第一系统空闲的概率：

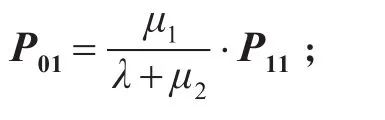
4）敌机突破防空系统的概率：

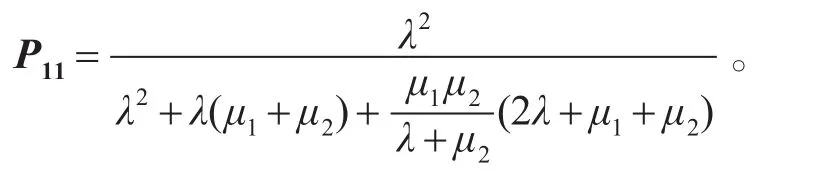
6 结语

排队论是一种仿真方法，具有层次精确细致的特点。将排队论恰当的应用于“抗击层”结构模型，仿真得出分层抗击的射击效率。目标的行动样式很多种，对于每一种目标行动的可能样式进行计算后，对比得出哪种射击方法（单层防空系统、由同类武器组成的多道防线防空、由不同类武器组成的多防线防空）效率最优，该方法克服了单纯用概率进行计算对来袭目标相互独立的限制，构成全程抗击防御系统，符合动态作战的实际。