铝硅酸盐矿物/石墨复合材料吸附甲基橙性能研究*

王恩文，叶绘英，余红英

(1.安顺学院 资源与环境工程学院，贵州 安顺市 561000；2.安顺学院 旅游学院，贵州 安顺市 561000)

印染废水中的染料虽然给人类社会带来色彩斑斓的世界，但其危害也极大，主要表现为：破坏水生生态系统，具有较强的环境累积效应、三致效应和生物毒性[1-3]。据不完全统计，我国由于染料废物所造成的水体污染占工业废水排放量的第5位，每年排放量约为20亿t。目前，我国印染废水回用率不到7%，若按1 t 印染废水污染20 t清洁水推算[4]，每年由于染料所带来的水体污染将为370亿t左右。因此，印染废水的治理刻不容缓、意义重大。

由于印染废水的可生化性差，在水中形成水合离子半径为10-12m数量级的污染物。而传统的物理、化学及生物方法对于此类污水的去除效率非常低，达不到预期效果，因而人们不断尝试新的治理方法，如光催化法[5]、膜分离法[6]、高能物理处理法[7]、超声波气振法[8]、MBR法[9]及UASB法等[10]。从处理效果看，无论是传统方法还是新工艺处理这类废水，均有其局限性，要么治污效率不高，要么是治污产污，不能从根本上解决日益加剧的环境污染问题。

本研究利用3种典型的铝硅酸盐矿物和石墨作为基材，以含甲基橙的印染废水为研究对象，制备一种可再生利用的高效复合材料，探讨其净化的技术方法与吸附机制，以期为后续制备一种可高效循环利用的矿物基吸附材料并用于净化复杂体系污染水体奠定理论基础。

1 材料与方法

1.1 主要试剂、原料及仪器

主要试剂为：羧甲基纤维素钠(CMC-Na，TP)，高氯酸(HClO4，GR)，浓硫酸(H2SO4，AR)，浓硝酸(HNO3，AR)，高锰酸钾(KMnO4，AR)，溴化钾(KBr，GR)，甲基橙(Methyl Orange，以下简称MO，AR)；所用的矿物材料分别为：组分A，主要矿物为累托石；组分B，主要矿物为偏高岭土；组分C，主要矿物为膨润土；组分D，主要为膨胀石墨。

主要实验仪器为：SRJX-4-13型高温马弗炉，HZQ-C型空气浴振荡器，ZW09X-Z型造粒机和UV-3000PC型紫外可见分光光度计等。

1.2 硅酸盐矿物/石墨复合材料的制备

铝硅酸盐矿物/石墨复合材料(aluminosilicate minerals/graphite composite，以下简称AGC)的制备方法：将组分A、B、C、D、粘结剂按质量比为40∶40∶25∶20∶18的比例混合均匀，再添加去离子水造粒(Φ8 mm)，于80℃烘箱中干燥8 h，而后再将温度升高至105℃干燥至恒重，调节升温速度为200℃·h-1，焙烧温度为800℃，焙烧4 h，便制得AGC。

1.3 样品测试及表征

AGC形貌结构分析测试采用德国蔡司公司Zeiss Ultra Plus型场发射扫描电子显微镜完成；红外光谱分析利用美国Nicolet公司的IS-10型傅立叶变换红外光谱仪完成；比表面积、孔径、孔体积等采用美国麦克公司ASAP2020M全自动比表面积及孔隙度分析仪；抗压强度采用美国MTS公司产MTS810型陶瓷试验机测试，其中加载速率为0.5 mm·min-1。

1.4 吸附性能评价

1.4.1 吸附效率

将100 mL待处理的含一定浓度的MO印染废水加入到250 mL锥形瓶中，再加入已知质量的AGC并将锥形瓶封口，放入恒温空气浴振荡器中反应一段时间(振荡频率为110 r·min-1)，后滤除AGC并将滤液以5000 r·min-1的速度离心5 min，用UV-3000PC型紫外可见分光光度计测定其中各残留MO的含量。并依式(1)计算AGC对MO的吸附效率：

(1)

式中，η为AGC对MO的吸附效率，%；c0为印染废水中各MO的初始浓度，mg·L-1；ce为吸附后废水中MO的残留浓度，mg·L-1。

由于未焙烧的AGC遇水后几乎全散，因此本研究未做焙烧前后AGC吸附性能对比研究。

1.4.2 吸附量

吸附量的评价依式(2)所示：

(2)

式中，qt为单位质量的AGC在t时刻吸附废水中MO的质量，mg·g-1；M为AGC用量，g。其中当ct为吸附MO达平衡浓度(ce)时，qt则可表示为AGC吸附废水中MO的平衡吸附量(qe)；当ct为最小残留浓度(cmin)时，qt则可表示为最大吸附量(qmax)。

2 AGC性能表征

2.1 物理性能

从表1中可知，AGC具有多孔性、低散失性，且抗压强度及比表面积均较大等特点。其中，低散失率(0.74%)和高抗压强度(2.53 MPa)特性对再生利用极为有利。如图1所示，按照IUPAC分类[11]，AGC的N2吸附-脱附等温线为Ⅲ型，表明待测样品主要存在较多的介孔(孔径范围为2～50 nm)及少部分的大孔(孔径大于50 nm的孔)[12]，且在5.0 nm附近呈现一个宽度较窄的尖峰，有利于特性吸附。另外，在0.52～0.95的高压区域存在H4型回滞环，与层状矿物堆积形成的狭缝型孔有关[13]。

表1 AGC物理性能测试结果

2.2 形貌结构分析

图2为800℃温度下焙烧成型的AGC外表面和横断面SEM图。结合图1分析可知，AGC既保持了基材中铝硅酸盐矿物的层状结构，又具有十分发育的微、介孔结构(由于高温焙烧使基材中有机物挥发，膨胀石墨氧化为CO2，以及表面吸附水、层间水、结构水的逸出而得到)。这就使得AGC在保持层状铝硅酸盐矿物良好的吸附性能外[14-15]，又由于大量孔道的形成，造成AGC内外表面形成晶格缺陷，成为不饱和键聚集区，该区实际上是一个能量过剩的活性区，具有极大的化学活性[13,16-17]。

2.3 官能团分析

AGC官能团分析是利用美国Nicolet公司的IS-10型傅立叶变换红外光谱仪进行测试分析(如图3所示)。波数3453 cm-1处为水分子中羟基的对称伸缩振动特征吸收峰；1633 cm-1为水分子H-O-H弯曲振动特征吸收峰，1085 cm-1和784 cm-1分别为材料中Si-O-Si的对称伸缩振动和弯曲振动特征吸收峰；677 cm-1为材料中Si-O-Al的伸缩振动特征吸收峰；611 cm-1和479 cm-1分别对应的是Si-O-AlVI弯曲振动和Si-O-Fe伸缩振动特征吸收峰[13,18-19]。综上可知，AGC官能团以层状硅酸盐矿物的基团为主且Fe元素含量较高。

图2 AGC的扫描电镜形貌

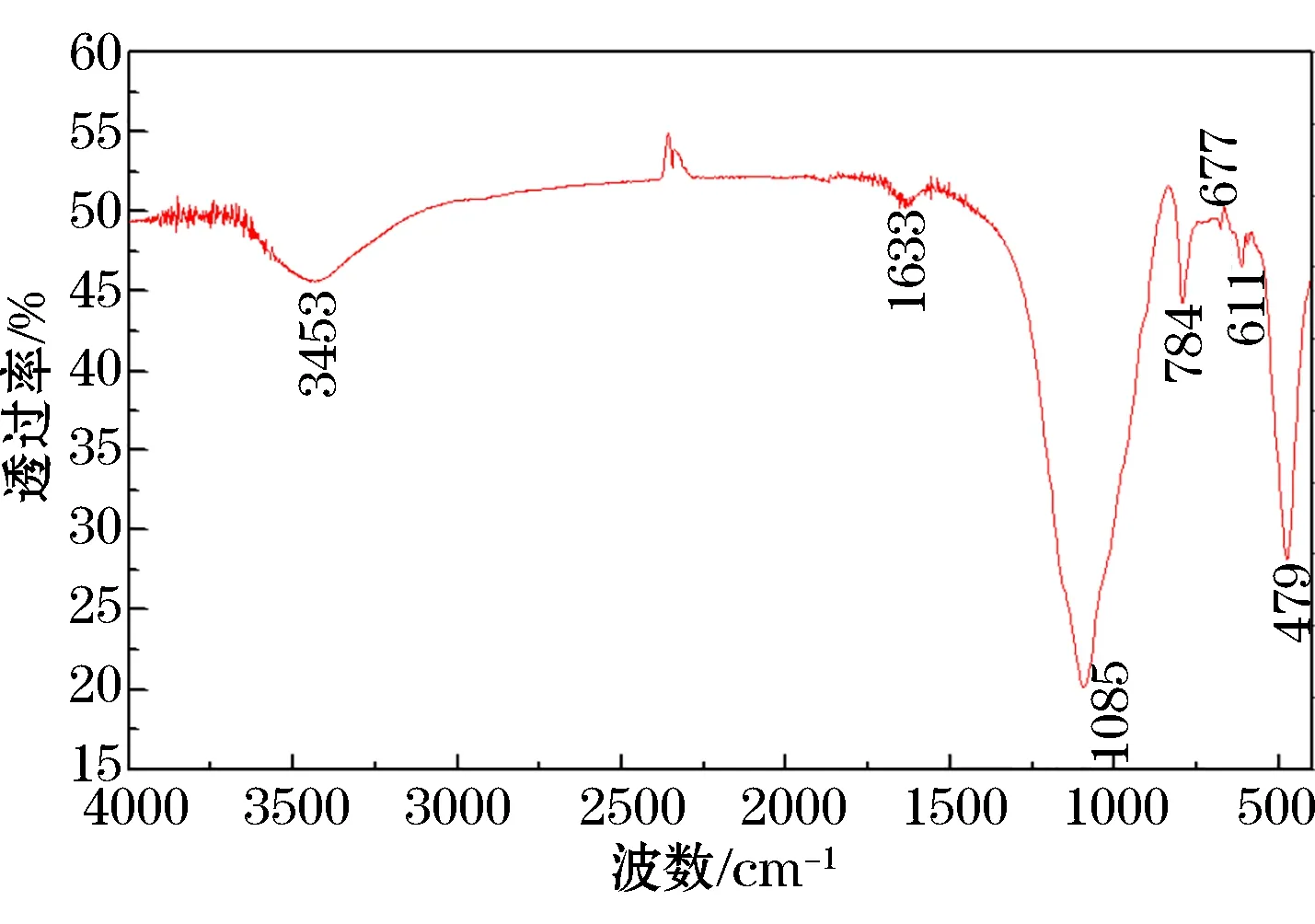
图3 AGC的傅立叶红外光谱

3 MO最大吸收波长和工作曲线的确定

3.1 最大吸收波长(λmax)的确定

由图4可知，对于MO溶液，在不同pH值条件下，显示出两个λmax值，即当pH值范围为4.0～12.0时，λmax= 464 nm，与自然条件下确定的λmax值相同，而当pH值范围为0.0～2.0时，λmax= 507 nm。

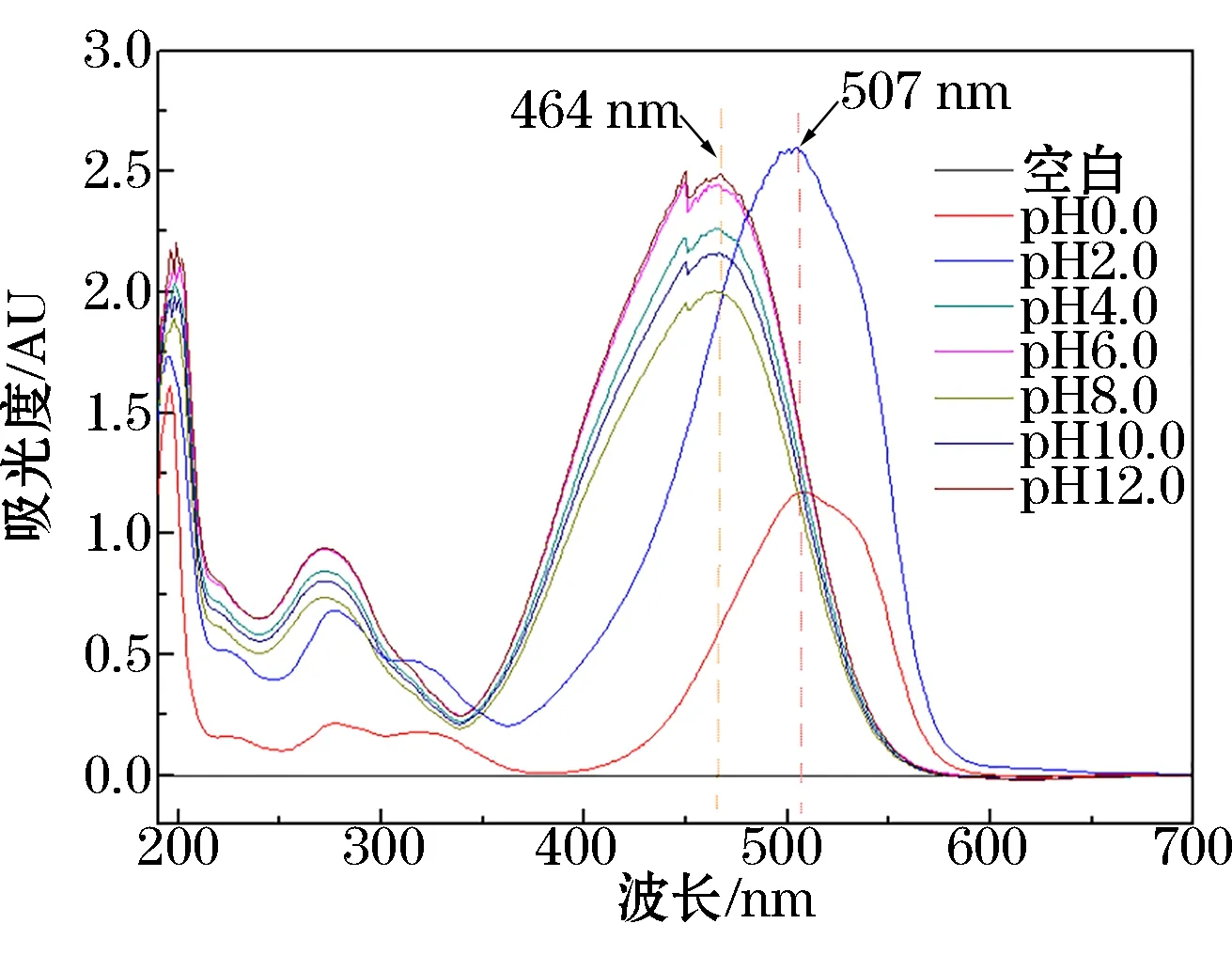
图4 pH值对MO溶液的UV-vis峰的影响

3.2 染料溶液标准曲线的确定

配制已知浓度梯度的MO溶液，利用图4确定的λmax测量分析，以确定不同浓度MO与λmax下吸光度之间的标准工作曲线(结果如图5所示)。

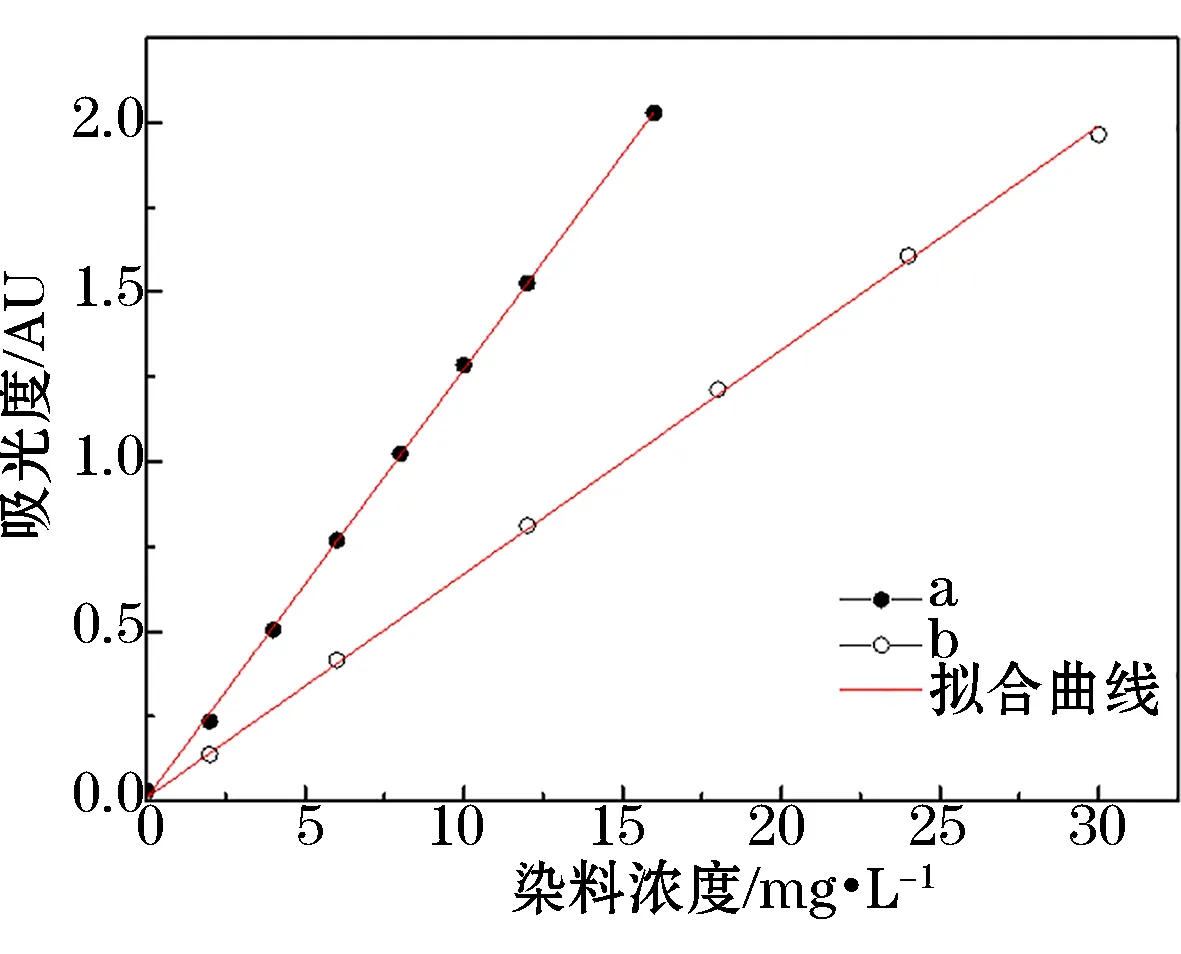
图5 MO溶液浓度梯度的标准曲线

由图6可得到MO在不同pH值范围内的浓度计算公式，结果如表2所示。

注：c为溶液中染料的浓度，mg·L-1；x为相对应的吸光度。

4 试验结果分析

4.1 AGC用量影响

取MO溶液(浓度为500 mg·L-1、pH值为6.44)100 mL于250 mL锥形瓶中，在空气浴振荡器中，调节温度为35℃，反应时间为48 h的条件下，分别调节AGC用量为1.0，2.5，5.0，7.5 g·L-1以及10.0 g·L-1，研究AGC用量对印染废水中MO的影响。结果如图6所示。

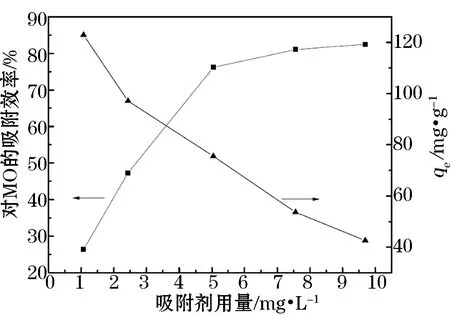
图6 AGC对MO吸附效率和平衡吸附量的影响

通过图6可以发现：

(1) 随着AGC用量的增加，MO的去除率显示出上升趋势(由1.04 g·L-1逐渐增加到9.95 g·L-1)，废水中MO的去除率从26.37%提升到82.50%，而qe则显示出明显地下降趋势(从122.88 mg·g-1下降到42.57 mg·g-1)；

(2) AGC对MO吸附时，以5.0 g·L-1为宜。

4.2 MO初始浓度影响

调节MO溶液的初始浓度分别为200，400，500，600，800 mg·L-1以及1000 mg·L-1，AGC用量为5.0 gL-1，其余条件同4.1节，研究MO初始浓度对AGC吸附性能的影响。结果如图7所示。

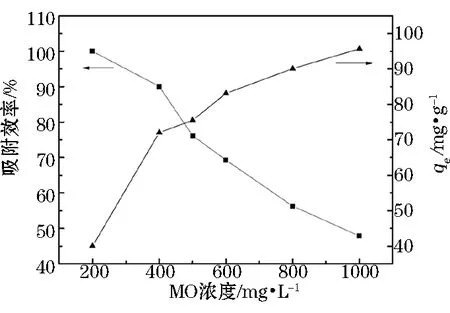
图7 MO初始浓度对AGC吸附效率和平衡吸附量的影响

从图7中可知，随着MO初始浓度提升，AGC的qe亦随之提高。这主要是由于吸附材料中的不饱和活性吸附位点与废水中的染料浓度之间存在的某种平衡关系引起的。主要表现为：

(1) 该用量的AGC吸附较低浓度的MO废水48 h后，其中的残留染料几乎完全被去除，此时材料中的不饱和活性吸附位点占主导；

(2) 当逐渐提升体系中染料的浓度，AGC中的不饱和活性吸附位点数急剧下降，染料的去除率亦急剧下降，而AGC的qe变化则趋于平缓。

因此，平衡关系可归纳为：在AGC总质量一定的情况下，不饱和活性吸附位点数量相当，则AGC的qmax一定，但qmax是一个理论值，只能随着体系中MO浓度的不断增加而无限趋近但很难达到，因此当MO初始浓度超过某一阈值时，AGC平衡吸附效率的下降趋势明显而qe提升变为缓慢。针对AGC，MO初始浓度的阈值为600 mg·L-1。

4.3 吸附时间影响

吸附试验总时间为48 h，调节时间间隔为2 h，MO溶液的初始浓度为600 mg·L-1，其余条件同4.2节。研究吸附时间对AGC吸附MO性能的影响。结果如图8所示。

由图8可知，AGC对MO的吸附可分为两个阶段：第一阶段为快速吸附阶段，主要是由于废水中染料向整个AGC外表面吸附引起的；第二阶段为缓慢吸附阶段，主要是由于吸附接近平衡后，废水中染料向AGC内表面吸附引起的[20]。AGC吸附MO两阶段分界点时刻为6 h，对应的吸附量(qt)为82.70 mg·g-1。

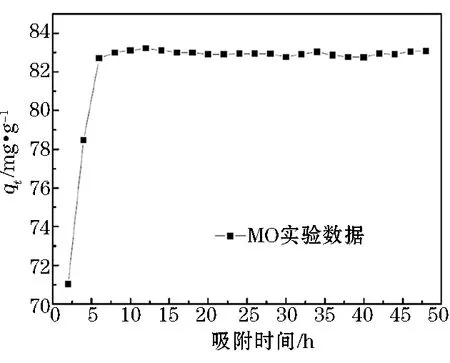
图8 吸附时间对AGC吸附量(qt)的影响

4.4 初始pH

调节MO溶液初始pH(pH0)分别为0.0，2.0，4.0，6.0，8.0，10.0，12.0，吸附时间为6 h，其余条件同2.5节。研究吸附时间对AGC吸附MO性能的影响。结果如图9所示。

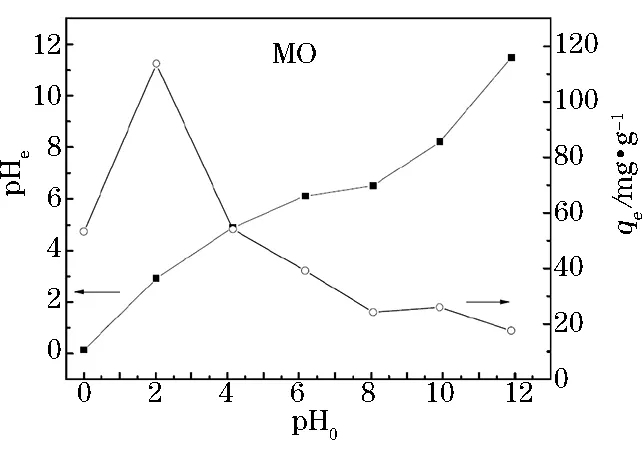
图9 pH0对AGC平衡吸附量(qe)和平衡pH(pHe)的影响

由图9可知，pH0对于AGC吸附料净化废水中MO确实影响显著，当染料废水pH0为2.0时，平衡吸附量曲线出现最大值，为113.74 mg·g-1，较废水原液的提高约37.5%。

4.5 AGC脱附再利用研究

将吸附饱和的AGC在750℃下焙烧1 h，而后按2.6节试验条件，调节MO溶液pH0为2.0，循环使用5次，结果如图10所示。

从图10中可知，脱附再生的AGC的吸附性能表现较佳，第5次再生后对MO的qe为101.73 mg·g-1，较初次使用的AGC仅下降10%左右，而平均质量损失率(散失率与烧失量之和)仅为5.78%。

4.6 吸附等温线分析

为研究“AGC—MO”表面的交互作用，本研究利用Langmiur和Freundlich两个常用的吸附等温线模型进行定量分析及预测，结果见图11和表3。

2种吸附等温线模型方程的描述如式(3)和式(4)。

Langmiur吸附等温线模型方程：

(3)

Freundlich吸附等温线模型方程：

(4)

式中，qe表示为单位AGC的平衡吸附量，mgg-1；ce表示为当吸附反应达到平衡时溶液中MO的浓度，mgL-1；qm表示为AGC表面单层吸附MO的最大容量，mgg-1；KL表示为Langmiur常数，L·mg-1；KF和n均是Freundlich吸附等温线常数，KF代表AGC吸附量大小的量(即当KF值越大，则吸附量越大)，由AGC/MO的特性、环境温度及AGC用量等决定，为有量纲常数，mg1-1/nL1/ng-1；n代表吸附模型的线性偏离度，与吸附液相/固相体系的性质有关，通常情况大于1，为无量纲常数。

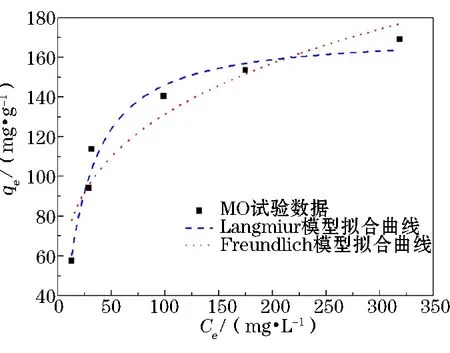
图11 AGC吸附MO的吸附等温线模型拟合(温度为 35 ± 1 ℃)

表3 AGC对MO的吸附等温线非线性拟合参数

结合图11与表3分析发现，Langmuir吸附等温线模型与试验数据的非线性拟合程度高于Freundlich的，且相关系数(R2)大于0.95，说明AGC对染料MO表现出良好的表面单层化学吸附[20]；用Langmuir吸附等温线模型对AGC吸附MO的曲线拟合数据来看，其最大吸附量(qmax, fitted)参数为170.83 mg·g-1，较试验的平衡吸附量(qe, exp)高，说明AGC对MO的吸附有一定的提升空间。

4.7 吸附动力学

采用准一级吸附动力学模型(Pseudo-first-order kinetic model)和准二级吸附动力学模型(Pseudo-second-order kinetic model)，对AGC吸附净废水中MO进行吸附动力学研究，结果如图12及表4所示。

2种吸附动力学模型方程的描述如式(5)和式(6)。

准一级吸附动力学模型方程：

qt=qe(1-e-k1t)

(5)

准二级吸附动力学模型方程：

(6)

式中，qt为t时刻单位AGC吸附MO的质量，mg·g-1；qe为平衡时单位AGC吸附MO的质量，mg·g-1；t为吸附时间，min；k1为准一级吸附动力学常数，min-1；k2为准二级吸附动力学常数，g·(mg·min)-1。

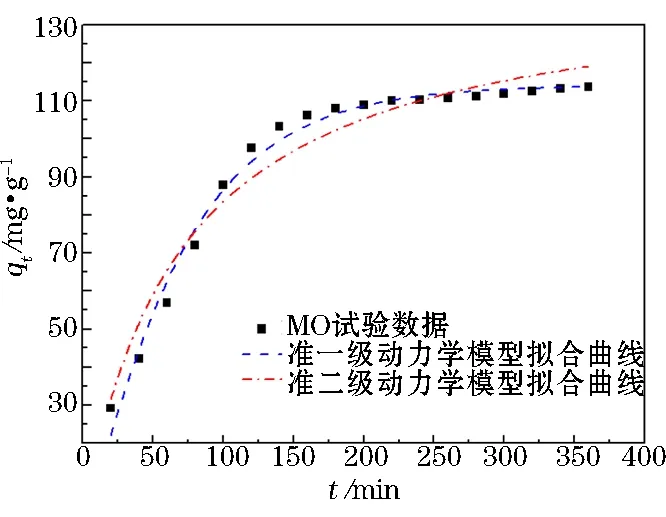
图12 AGC对MO的吸附动力学模型曲线(温度为 35 ± 1 ℃)

分析图12及表4可以发现，准一级动力学模型与试验数据的非线性拟合程度更佳，相关系数(R2)大于0.98，且通过准一级动力学模型得到的平衡吸附量理论计算值(qe1)与试验数据更接近，进一步说明准一级动力学模型更适宜用于描述AGC吸附MO随时间变化的行为过程。

表4 AGC吸附MO的动力学模型拟合参数

4.8 吸附热力学

通过不同温度(288，298，308，318 K)条件下AGC吸附MO的数据分析，计算出相关热力学状态参数，即吉布斯自由能变(ΔGθ)、熵变(ΔSθ)、焓变(ΔHθ)3个参数，计算式可参见公式(7)和公式(8)。

ΔGθ=-RTln(106KL)

(7)

ΔGθ=ΔHθ-TΔSθ

(8)

式中，R[8.314 J·(mol·K)-1]为气体常量；T为开氏温度，K；KL为Langmiur常数，L·mg-1。

AGC对MO的吸附热力学分析详见图13和表5。在15℃～45℃温度试验条件下，AGC热力学参数为：ΔGθ小于零、ΔHθ小于零、ΔSθ大于零，说明其对于MO的吸附能自发地进行。另外，ΔHθ小于零，说明该吸附属于放热过程。

图13 AGC吸附MO的吉布斯自由能与温度关系

表5 AGC吸附MO的热力学参数

5 结 论

本研究以3种铝硅酸盐矿物和石墨为基材制备了一种复合材料(AGC)，其具备多孔径分布、大比表面积、低散失率等优良特性，保留了层状铝硅酸盐矿物高吸附性能的官能团，且避免了粉体材料回收困难易于形成二次污染的问题，但再生吸附效率有待进一步研究提升。AGC对于阳离子染料(MO)的吸附等温线符合Langmiur模型，吸附动力学遵从准一级动力学模型。吸附热力学参数分别为ΔGθ<0、ΔHθ<0、ΔSθ>0，说明了吸附体系为放热反应，且在15℃～45℃温度下加热有利于反应自发进行，揭示了增加吸附体系温度，有利于材料吸附官能团的活化和吸附位点的增加。