立足“素养立意” 灵动“问题解决”
——数量关系运用中提高学生解决问题能力的实践研究
浙江杭州市萧山区靖江第一小学(311221) 徐华锋
学生数学能力“缺失”的重要原因是缺乏思维的方法,缺乏解决问题的策略。教学中,教师要采取有效策略,对学生进行逻辑思维训练,引导学生从问题本身的内在逻辑关系(数量关系)入手,厘清解题的思路,激发学生数学思维的原点,从而有效培养学生解决问题的能力。那么,如何做到“春种一粒粟,秋收万颗子”呢?
【策略一】“借东风”——借助情境,强化体验
1.从情境中体验数量关系
与问题解决有关的题目一般都是由情境和数量关系两方面组成的,其中数量关系是问题求解的关键,情境是指条件和问题的表达方式,是影响学生理解数量关系的重要因素。问题的解决,在于透过情境把握数量关系,进而确定算法。问题解决的教学,要使学生经历掌握数量关系的过程,经历对较复杂的数量关系进行分析综合、抽象概括和判断推理的过程。
如三年级上册的“解决问题”:小明的妈妈在统计自己的手机流量,她发现上周用了386兆流量,这周用的流量是上周的2倍。小明的妈妈两周一共用了多少兆流量?
教师可引导学生按下列步骤解决问题:
(1)分析数量关系:上周用的流量+这周用的流量=两周一共用的流量,列出算式:386+386×2=386+772=1158(兆)。
(2)如果把上周用的流量看作1份,那么这周用的流量则是 2 份,列式:386×(1+2)=386×3=1158(兆)。
(3)想一想:我们是怎样解决问题的?(使学生在这样的情境中感悟上周用的流量、这周用的流量与两周一共用的流量三者之间的关系)
实际教学显示,在良好的教学情境下,学生解决问题时不是把问题和类型相联系,而是将情境中的问题与运算相联系。因此,教师不必在语言上做太多的强化,而是应该为学生提供真实又熟悉的情境,让学生在情境中自主探索和体验问题里的数量关系。
2.从体验中概括数量关系
生活和工作中随处都有数量关系,人们常常利用数量关系去认识事物、分析事物,用数量关系去解决问题。因此,数量关系的概括是学生学习数学的必备技能。教师要有目的地进行教学,让学生了解常见的数量关系式,如“单价×数量=总价”“速度×时间=路程”等,学生对这些数量关系比较熟悉,在充分体验和感悟的基础上能够自主概括出来,从而留下深刻印象。
例如,教学“单价、数量、总价”时,我先用课件出示一个花店的情境图,然后引导学生依次解决以下问题:
(1)自己提出问题并尝试解决,在解决问题的过程中感悟单价、数量和总价的含义。(如:小红买3枝菊花,需要多少元钱?再买1枝百合花,一共需要多少元钱?)
(2)简要概括单价、数量、总价之间的关系。
(3)请设计一个配花方案,用于布置国庆联欢会会场,价格不超过80元。你会怎样配?
通过实际体验,学生不但理解了单价、数量和总价的含义,而且感受到了运用“单价×数量=总价”这个数量关系式的重要性。
【策略二】“联纵横”——数形结合,有机联合
数形结合是通过数与形的相互转化、相互对应关系来解决数学问题的一种数学思想方法。数形结合,可将抽象的数学与直观的图形相结合,或从直观的图形中概括抽象的数学。著名数学家华罗庚说过:“数缺形时少直观,形少数时难入微。”在教学数量关系时,可以借助图形的性质,将数与形结合起来,使抽象的概念和关系直观化、形象化,帮助学生有效分析数量关系,提高问题解决的正确率。
1.从“形”到“数”,逐步建立数学模型
由于年龄和心理发展的特点,学生的数学思维需经历从形象直观逐步走向抽象的过程,因此教师在教学中要引导学生从直观的图形演示和对比中寻找数学知识内在的联系,从而构建问题解决的基本模型。
如教学“一个数是另一个数的几倍”的应用题时,我校一位教师是这样设计的:
师(谈话引入):六一儿童节快到了,老师想和小朋友一起装扮我们的教室。你们看老师准备了什么?
师:谁能说一说这两种花之间的关系?
生1(预设):相差关系。红花比蓝花多4朵,蓝花比红花少4朵。
生2(预设):相加关系。红花和蓝花一共有12朵。
生3(预设):倍数关系。红花的数量是蓝花的2倍。
师:为什么说红花的数量是蓝花的2倍呢?这节课我们一起来学习倍数的有关知识。
生4(预设):蓝花有4朵,红花有2个4朵,8÷4=2。
生5(预设):把蓝花的数量看成1份,红花的数量则为 2 份,8÷4=2。
师(变一变):蓝花数量不变,红花变成12朵,这时红花的数量是蓝花的几倍?
师:生活中还有哪些现象也存在倍数关系?
生6(预设):我得了9颗智慧星,王玲得了3颗,我得的智慧星数量是王玲得的3倍。
生7(预设):我今年8岁,妈妈32岁,妈妈的年龄是我的4倍。
师:刚才大家列举了生活中一些类似红花和蓝花倍数关系的现象,现在我们再看大屏幕。
师:把花朵放到长方形里,我们很容易看出红花的数量是蓝花的2倍。想一想,除了红花和蓝花,把什么放到这些长方形里,也能形成倍数关系?
生8(预设):第一行的两个长方形里可以各放4个苹果,第二行的长方形里放4个梨。
师:苹果的个数是梨的几倍?列出算式。(8÷4=2)
师:物品的种类和数量还可以怎样变呢?
生9(预设):在第一行的每个长方形里放6元钱,一共12元,在第二行的长方形里放6元钱。
师:第一行的钱是第二行的几倍?(12÷6=2)
师:刚才不管大家怎么改变数量或物品的种类,算出的倍数都是2,这是怎么回事?(都是把第二行看成一份,第一行有这样的2份,所以它们总是存在2倍的关系)
师:第二行的蓝花数量不变,第一行变成这样的4份(如下图)。现在红花的数量是蓝花的几倍?列出算式。(16÷4=4)
师:第一行还可以怎样变?(长方形的数量可以变,每个长方形里的花朵的数量也可以变)
师(小结):我们刚才研究的都是两个数之间的数量关系,而且都是把其中一个数看成1份,另一个数有这样的几份,就是几倍,即找到比较的两个数→明确把哪个数看成1份→看另一个数中含有这样的几份,可以用除法来计算(求出倍数)。
该教学设计层层深入,能引导学生在图形的变化与比较中深刻理解倍数关系,从而有效构建“一个数是另一个数的几倍”的思维原型,即“一个数÷另一个数”。
2.从“数”到“形”,有效激发学生思维
研究表明,低年级学生主要是凭借事物的具体形象来进行直观思维活动的,而在解决问题时所明确的数量关系通常需要通过抽象思维来理解。这是解决问题教学中的一个突出矛盾,若能把抽象的数量关系用恰当的、形象的图形表示出来,就可以解决这一矛盾,同时激发学生的数学思维。
如,题目:一桶油,连桶共重20千克,吃掉一半油后,剩下的油连桶重11千克。吃掉了多少千克油?原来一桶油重多少千克?
从条件来分析:桶和油之间到底存在什么样的数量关系?吃掉一半油后,桶和油之间又是一种什么样的数量关系?低年级学生大都感觉此类数量关系抽象,但在我改用图形(如下图)表示它们之间的数量关系后,学生马上就明白了桶和油之间的关系,然后巧妙地解决了这个问题。
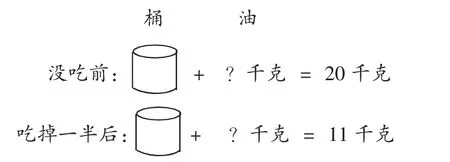
可以发现,在解决问题的教学中充分渗透数形结合的思想,把抽象的数量关系用恰当的图形直观地表示出来,有助于提高学生思考问题和解决问题的能力,事半功倍。
又如,题目:医院包扎用的三角巾是底和高都为9分米的等腰直角三角形。现在有一块长75分米、宽18分米的白布,最多可以做这样的三角巾多少块?
学生往往会根据经验“总面积÷一块的面积”,列出算式 75×18÷(9×9÷2),但这并不符合实际情况。为了让学生进一步理解“密铺”问题的解题思路,我引导学生通过画图进行模拟操作:
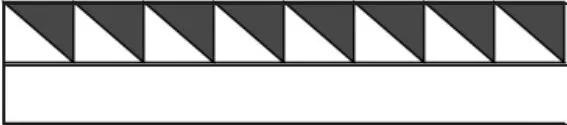
由图可知,可以将这块白布沿宽平均分成两份,每份可以做16块三角巾,因此这块白布一共能做这样的三角巾16×2=32(块)。如此,学生很容易就理解和掌握了“密铺”的数学思想方法。
数形结合的方法能够很好地促进学生联系生活实际,灵活解决数学问题,同时能有效地防止学生生搬硬套,开阔学生的解题思路,从而提高学生解决问题的能力。教师要有效利用数形结合的方法,不失时机地为学生提供恰当的材料,引导学生将抽象的数量关系具体化,把抽象的解题思路形象化。这样不仅有利于学生顺利、高效地学好数学知识,还有助于学生学习兴趣的培养、学习能力的增强,最为关键的是能够帮助学生有效构建基本的数学思维模型。
【策略三】“慎读之”——有效读题,正确解答
解决问题能力的培养中,除了“情境体验”和“数形结合”这两种有效的训练方式以外,有效读题,正确理解题意,也是提高学生问题解决能力的一种有效方法。
1.据题目情境,寻找对应模型
例如,对于题目“一辆汽车从甲地开往乙地,开了2.5小时,已知该车每小时行驶52千米,甲、乙两地相距多少千米?”,我这样引导:
(1)想一想,这是关于什么问题的应用题?(行程问题)
(2)行程问题有什么数量关系?(速度×时间=路程)
(3)题目要求的是哪个量?(路程)要求这个量,需要知道哪些条件?(速度、时间)
(4)尝试根据找到的相关“量”的数据,列式解答。
2.从关键字词入手,建立等量关系
应用题中往往隐含着一定的数量关系,而一些关键字词,如是、等于、相当于之类的字词,则有助于学生正确把握题目中的数量关系。因而在教学中,教师应该积极引导学生将这些关键字词用数学特有的形式(数量关系式)表示出来。
例如,对于题目“小军爸爸今年36岁,是小军年龄的2倍,小军今年几岁?”,我这样引导:
(1)找出题目中表明两者关系的字词。(是)
(2)联系前后,找出小军爸爸的年龄和小军的年龄的关系。
(3)列式解答。
3.顺应逻辑顺序,找准数量间的关系
学生在读题时,准确捕捉数量间的关系是问题解决的关键。教师要引导学生在读题时从中提炼出已知条件和所求问题,厘清各个量之间的关系,然后用式子表示出来。
如,解答“第一车重1650千克,比第二车重1/10,第三车比第二车轻1/12,第三车重多少千克?”这个问题时,要求学生边读题边顺着题意思考,读完之后,再捋一捋解题思路:要求“第三车”,得先求出“第二车”;分析前两个已知条件,发现单位“1”未知,需要用除法解决。一来二去,反复推敲,数量关系就会慢慢浮现出来了。
在数学问题的解决中,数量关系是激发学生思维的基点,只有把“数量关系”厘清,才能有效培养学生问题解决的能力。在数学课堂教学中,教师要正确解读教材,扬长避短、博采众长,渗透数学思想,既要避免一味地对过去全盘否定,又要避免“穿新鞋走老路”,只有强化学生的数量意识,有效构建数学模型,才能真正促进学生解决问题能力的提高,也才能促进学生达到“稻花香里说丰年,听取蛙声一片”的境界。

