40CrNiMo钢的热变形特征及变形抗力模型
,,,,
(西安建筑科技大学冶金工程学院,西安 710055)
0 引 言
40CrNiMo钢是一种中碳Cr-Ni-Mo系钢,其综合力学性能较好、淬透性高、抗过热稳定性强、韧性好、生产工艺较简单,广泛应用于制造受冲击载荷较高、断面尺寸较大的零部件,如汽轮机和喷气式客机的起落架、大型发电机转子、喷气涡轮机轴及其他结构部件等[1-2]。变形抗力是材料在高温下的基本属性,受变形温度、变形程度、应变速率和材料化学成分的影响,同时也是材料显微组织演变的综合反映[3],因此研究材料的热变形特征是非常重要的。热变形过程中发生的动态再结晶、动态回复和超塑性行为均有利于材料的加工,尤其是发生动态再结晶区域的变形耗散效率较高,该区域对应的变形温度和变形速率更有助于材料的均匀变形和获得预期的组织[4]。根据变形抗力的影响因素,变形抗力模型可分为两种:一种为涉及热激活、位错运动等微观机制的变形抗力模型;另一种为直接考虑变形温度、应变速率和应变等宏观物理量对流变应力影响的变形抗力模型[5]。通过对金属塑性变形理论的研究和钢变形抗力模型的分析比较[6-13],发现特列齐亚可夫·久津模型[12]和周纪华-管克智模型[13]的发展较为成熟。目前,国内外有关40CrNiMo钢热变形特征和变形抗力模型的研究鲜有报道。因此,作者采用Gleeble-3500型热模拟试验机对40CrNiMo钢进行了单道次热压缩试验,得到了该钢在不同变形温度和应变速率下的流变应力-应变曲线,分析变形温度、应变速率对其热变形组织的影响;用特列齐亚可夫·久津模型、周纪华-管克智模型对试验数据作线性回归建立了40CrNiMo钢的变形抗力模型,为40CrNiMo钢热变形工艺的制定提供理论依据。
1 试样制备与试验方法
试验材料为40CrNiMo钢,由某特钢公司提供,化学成分如表1所示。试验钢在电炉冶炼后铸成钢锭,将钢锭开坯加热、保温、锻后坑冷,然后在DK7740C型数控电火花线切割机床上切成尺寸为φ10 mm×15 mm的热压缩试样。

表1 40CrNiMo钢的化学成分(质量分数)Tab.1 Chemical composition of 40CrNiMo steel (mass) %
在Gleeble-3500型热模拟试验机上对试样进行单道次热压缩试验。先将试样以10 ℃·s-1的升温速率加热到1 150 ℃,保温3 min,然后以5 ℃·s-1的降温速率将试样冷却到800,900,1 000,1 110 ℃,保温30 s后分别以0.1,1,10,50 s-1的应变速率进行压缩变形,变形量为60%,压缩变形结束后立即水冷,以保留不同温度下的变形组织。
沿试样压缩方向纵向剖开,经机械研磨、抛光后,将试样浸泡于75 ℃的由50 mL过饱和苦味酸水溶液和3 mL餐具洗洁精组成的混合溶液中,以显示其原奥氏体晶界,采用GX51 Olympus型光学显微镜观察其显微组织。
2 试验结果与讨论
2.1 应力-应变曲线
从动态软化机制的角度考虑,将金属材料在热变形过程中的应力-应变曲线分为动态回复型和动态再结晶型[14-15]。由图1可以看出:当应变速率为0.1 s-1时,变形温度在800~900 ℃时的应力-应变曲线为动态回复型,变形温度在1 000~1 100 ℃时的为动态再结晶型;当变形温度为1 000 ℃时,应变速率为0.1 s-1时的应力-应变曲线为动态再结晶型,应变速率为1~50 s-1时的为动态回复型;当应变速率为50 s-1时,高的应变速率使得加工硬化与动态回复和动态再结晶的竞争不稳定,导致应力-应变曲线出现明显的波动。由于热模拟试验机的局限性,未得到变形温度1 100 ℃、应变速率50 s-1条件下的应力-应变曲线。
由图1还可以看出,在热压缩过程中,随着应变的增大试验钢历经加工硬化、流变软化、稳态流变、再次加工硬化等4个阶段。在变形初期,流变应力随着应变的增加而迅速增大,试验钢发生加工硬化,这是因为此时外加应力使组织中的位错密度增大,位错滑移受到阻碍而造成的;当变形程度较低时,随应变的增加,流变应力缓慢增大至峰值,该阶段为流变软化阶段,此时晶粒内部的储存能较小,试验钢仅发生了轻微的动态回复,加工硬化作用远大于软化作用;随着应变的继续增加,流变应力趋于平稳,此时组织中的位错密度继续增大,位错发生滑移和攀移,在变形激活能的作用下,加工硬化与动态回复软化逐渐趋于平衡,或是动态再结晶和动态回复软化过程与加工硬化过程达到动态平衡,从而进入稳态流变阶段;随着应变的继续增加,由于位错的增殖,加工硬化作用大于软化作用,流变应力开始略微增加,试验钢出现再次加工硬化现象[16]。
2.2 显微组织
2.2.1 变形温度的影响

图1 试验钢在不同应变速率和变形温度下的真应力-真应变曲线Fig.1 True stress-true strain curves of the tested steel at different strain rates and deformation temperatures

图2 应变速率为10 s-1时不同变形温度下试验钢的显微组织Fig.2 Microstructures of the tested steel at different deformation temperatures and strain rate of 10 s-1
由图2可以看出:当变形温度为800 ℃时,原奥氏体晶粒沿着变形方向被明显拉长,晶界处出现少量的链条状再结晶晶粒,即试验钢仅发生了部分动态再结晶,大部分晶粒处于动态回复状态;当变形温度为900 ℃时,试验钢中出现大量再结晶晶粒,但仍存在少量未发生动态再结晶的粗大原奥氏体晶粒,这是由于随着变形温度(800 ~900 ℃)的升高,合金元素在奥氏体中的固溶度增大,晶界附近析出的碳化物减少,导致阻碍动态再结晶的能力逐渐减弱,从而形成更多的再结晶晶粒;当变形温度在1 000~1 100 ℃时,试验钢发生完全动态再结晶,而且随着变形温度的升高,动态再结晶晶粒长大。在相同应变速率下,随着变形温度的升高,合金元素的扩散速率增大,原子间的结合能降低,位错滑移、攀移所需的能量降低,变形储能增加,动态再结晶的孕育期缩短,晶粒长大的时间变长,因此试验钢的再结晶晶粒长大。
2.2.2 应变速率的影响
由图3可以看出:当应变速率为0.1 s-1时,原奥氏体晶粒发生明显的塑性变形,晶粒内及晶界附近出现少量的变形带,未出现再结晶晶粒;当应变速率为1~50 s-1,沿原奥氏体晶界分布的链条状再结晶晶粒增多,这是由于较高的应变速率使原奥氏体晶粒在很短时间内累积了大量的位错、变形带等缺陷,加工硬化效果减弱,形成的位错塞积、交割等进一步阻碍位错滑移,增加了形变储能,导致再结晶的驱动力增加而造成的。

图3 变形温度为800 ℃时不同应变速率下试验钢的显微组织Fig.3 Microstructures of the tested steel at different strain rates and deformation temperature of 800 ℃
2.3 动态再结晶激活能和Zener-Honomon参数
Zener-Honomon参数可描述在热变形过程中不同峰值应力下,变形温度与应变速率之间的关系[17-18],其表达式为
(1)
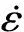
式(1)两边取对数,整理可得
(2)
(3)
当变形速率一定时,式(2)两边对1/T求偏导数,可得
(4)

综上可知,40CrNiMo钢的Zener-Honomon参数可以表示为
(5)
2.4 变形抗力模型的建立
周纪华-管克智模型为


(6)
T′=(t+273)/1 000
(7)
式中:σ为变形抗力,MPa;t为变形温度,℃;σ0为变形温度为1 000 ℃、应变为0.4、应变速率为10 s-1时的变形抗力,MPa;a1,a2,a3,a4,a5,a6均为材料常数。

图4 试验钢和σp-1/T的关系曲线Fig.4 Relation curves of and σp-1/T of the tested steel
特列齐亚可夫·久津模型为
(8)
式中:A,a,b,c,d均为材料常数;ε为应变。
根据式(6)与式(8)中变形抗力与变形温度、应变、应变速率之间的关系,对图1中的数据进行非线性拟合,得到式(6)和式(8)中的材料常数,如表2和表3所示。

表2 式(6)中材料常数的拟合结果Tab.2 Fitting results of material constant in equation (6)

表3 式(8)中材料常数的拟合结果Tab.3 Fitting results of material constant in equation (8)
将表2和表3中的材料常数分别代入式(6)和式(8),再将应变代入式(6)和式(8),得到变形抗力的计算值,并与试验值进行比较,发现:周纪华-管克智模型计算得到的变形抗力的最大相对误差为15.29%,平均相对误差为4.82%;特列齐亚可夫·久津模型型计算得到的变形抗力的最大相对误差为28.39%,平均相对误差为6.85%。由此可知,周纪华-管克智模型更能准确地描述40CrNiMo钢热变形时不同参数之间的关系,可为实际生产过程中轧制压力的确定提供参考。
综上可知,40CrNiMo钢的变形抗力模型可表示为
σ=169.70exp(-2.360 0T′+3.074 4)×

(9)
3 结 论
(1) 在较低的应变速率(0.1 s-1)和较高的变形温度(1 000~1 100 ℃)下,试验钢的应力-应变曲线均为明显的动态再结晶型;当应变速率为50 s-1时,应力-应变曲线出现明显的波动;在热压缩过程中,随应变的增大,试验钢依次出现了加工硬化、流变软化、稳态流变、再次加工硬化等4个过程。
(2) 当变形温度为800 ℃时,应变速率的增大使动态再结晶晶粒增多;在应变速率为10 s-1条件下,当变形温度由800 ℃升至900 ℃时,再结晶晶粒增多,当变形温度为1 000 ℃时,试验钢发生了完全动态再结晶,当变形温度为1 100 ℃时,动态再结晶晶粒长大。
(3) 试验钢的动态再结晶激活能为322.53 kJ·mol-1;应变速率为0.1~50 s-1、变形温度为800~1 100 ℃条件下,由周纪华-管克智模型计算形抗力的平均相对误差为4.82%,由特列齐亚可夫·久津模型得到的为6.85%,周纪华-管克智模型的精度更高。

