一定干密度状态下路基膨胀土数学模型的建立
文/黄凯 湖南省第二工程有限公司 湖南长沙 410015
1、引言
位于膨胀土地图的路基由于膨胀土含水较多,容易产生开裂等破坏现象,因此对于一定干密度状态下路基膨胀土建立数学模型显得十分必要[1,2],本文提出了基于拟合方法的数学模型,对数学模型的建立过程进行了详细介绍和推导。
2、数学模型的建立
分别选用不同产地的路基膨胀土为实验原料,分别记为1#土,2#土和3#土,在一定干密度条件下,膨胀土含水比率和膨胀土负载压力对其吸湿膨胀产生的变形影响最大,这种变形存在两种极限状态,即无负载条件下的膨胀率和膨胀力。采用相对变形和相对压力作为参考,将膨胀率和负载压力、含水比率相关联,相对形变为负载膨胀率εs和无负载膨胀率εm的比值,同理,相对压力为负载压力P和膨胀力Pm的比值。统计不同产地的路基膨胀土(土性和干密度不同,1#、2#、3#的干密度分别为1.68g/cm-3、1.72g/cm-3和1.93g/cm-3)的在不同含水比率(w0)条件下的相对膨胀率和相对压力,采用双曲线函数进行拟合可以得出如表1所示的关系:

表1 不同路基膨胀土相对膨胀率和相对压力的拟合结果
从表1所示的拟合结果可以看出,1#-3#膨胀土的εs/εm和P/Pm之间的函数关系为双曲线函数,同时,对于不同含水比率的土样来说,这种函数关系并未收到影响,说明在不同含水比率条件下,εs和εm之间具有相似的关系。
总结表1的结果,可以得到εs和εm之间的关系式,如式1所示:
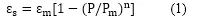
其中拟合系数用n表示,n只和土样的土性和干密度有关。
采用相同的方法,对三种土样的εm和w0进行拟合,拟合结果如表2所示:

表2 不同路基膨胀土无负载膨胀率和含水比率的拟合结果
根据拟合结果得到εm和w0的关系式,如式2所示:
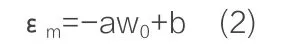
采用相同方法得到Pm和w0的关系式,如式3所示,拟合结果见表3:

表3 膨胀力和含水比率的拟合结果

吸湿膨胀率ε与负载膨胀率εs之间的关系 [3]为 ε=εs·(w-w0)/(ws-w0), 其中ws是路基膨胀土在负载条件下吸收饱和水状态后含水比率,w为路基膨胀土在吸收水分过程中的含水比率,土样负载条件下吸收饱和水状态后含水比率ws和初始土样密度ρ0、体积质量Gs以及负载膨胀率εs存在一定的关系式,即ws=(1-ρ0/Gs+εs)/ ρ0,将上述关系式和式1-3结合,即可得到一定密度状态下路基膨胀土的数学模型,如式4所示:
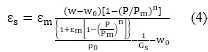
结论:
综上所述,本文对三种路基膨胀土样的数据进行拟合获得函数关系式,结合获得的函数关系得到了一定干密度状态下的路基膨胀土数学模型,该模型参数较少,在对膨胀土做路基进行形变计算时,较为简单,同时该模型可以覆盖极限条件,例如P和Pm相等、ε和εm相等、ε=0、P=0。

