基于空间应用的TTE时钟同步算法研究

，

(北京控制工程研究所，北京 100190)

0 引言

近些年来，在许多关键领域比如航天航空、工业控制等对实时性提出了更高的要求。广泛应用于航空领域的航空电子全双工交换式以太网(avionics full duplex switched ethernet, AFDX)[1]采取了一些措施提高了在一些关键领域的时间确定性[2]，但由于其还是事件触发的机制，并不能保证完全的时间确定性。时间触发以太网(time-triggered ethernet, TTE)作为新型的分布式交换网络，在普通以太网的基础上增加时间触发机制，解决了普通以太网中时间不确定性问题，具有强实时、高带宽、高安全性的特点，是下一代航天航空数据网络的重要发展方向。

TTE网络要想实现时间触发以及实时调度的功能，关键在于建立一个全局统一同步的时钟。只有在保证一定精度范围内的时钟同步的前提下，才能使各个节点在规定的时刻正确收发数据消息。因此研究TTE时钟同步算法成为实现TTE网络的关键之一，然而，目前国内外对于TTE时间补偿算法研究较少，AS6802 协议[4]虽然对TTE 的时钟同步模式进行了描述，并对协议中关键的流程比如时间同步过程、固化以及压缩算法等进行了详细介绍，但却没有为时钟同步提供具体的补偿方法。

本文的工作在于首先分析了TTE时间同步过程，以及时间同步过程中存在的不确定性，这些不确定性会直接影响时间同步精度，并建立了时钟模型以及不确定性带来的抖动噪声数学模型，根据噪声的统计特性采用了kalman滤波等三种滤波算法，得到了较好的效果。最后在滤除噪声的影响之后，采用了两种渐进时钟补偿方法对时钟进行了补偿，并通过仿真分析验证了算法的可行性。

1 TTE时钟同步分析

1.1 时钟同步过程

TTE网络时钟同步节点主要分为三种：CM节点、SM节点以及SC节点，时钟同步过程如图1所示。

1)SM在sm_dispatch_pit时刻提交PCF帧，并在sm_send_pit时刻发送PCF帧。

2)CM 在cm_receive_pit时刻接收到来自SM的PCF帧，并且使用时钟固化算法，使得PCF的接收顺序和其发送顺序一致，得到时钟固化点cm_permanence_pit。

3)CM 使用时间压缩算法计算时间偏差的均衡值cm_cr。

4)CM 根据PCF的预计接收时间cm_scheduled_pit 以及均衡值cm_cr计算得到时钟偏差并进行修正，然后在cm_dispatch_pit时刻提交PCF帧，在cm_send_pit发送新的整合的PCF帧。

5)SM/SC 在smc_receive_pit 接收到新的CM发送来PCF帧之后，采用时间固化算法保证 PCF的接收顺序和其发送顺序一致，得到固化时间smc_permanence_pit。

6)SMC根据预计接收时间smc_scheduled_pit以及实际固化时间smc_permanence_pit得到时钟偏差，进行时间补偿。

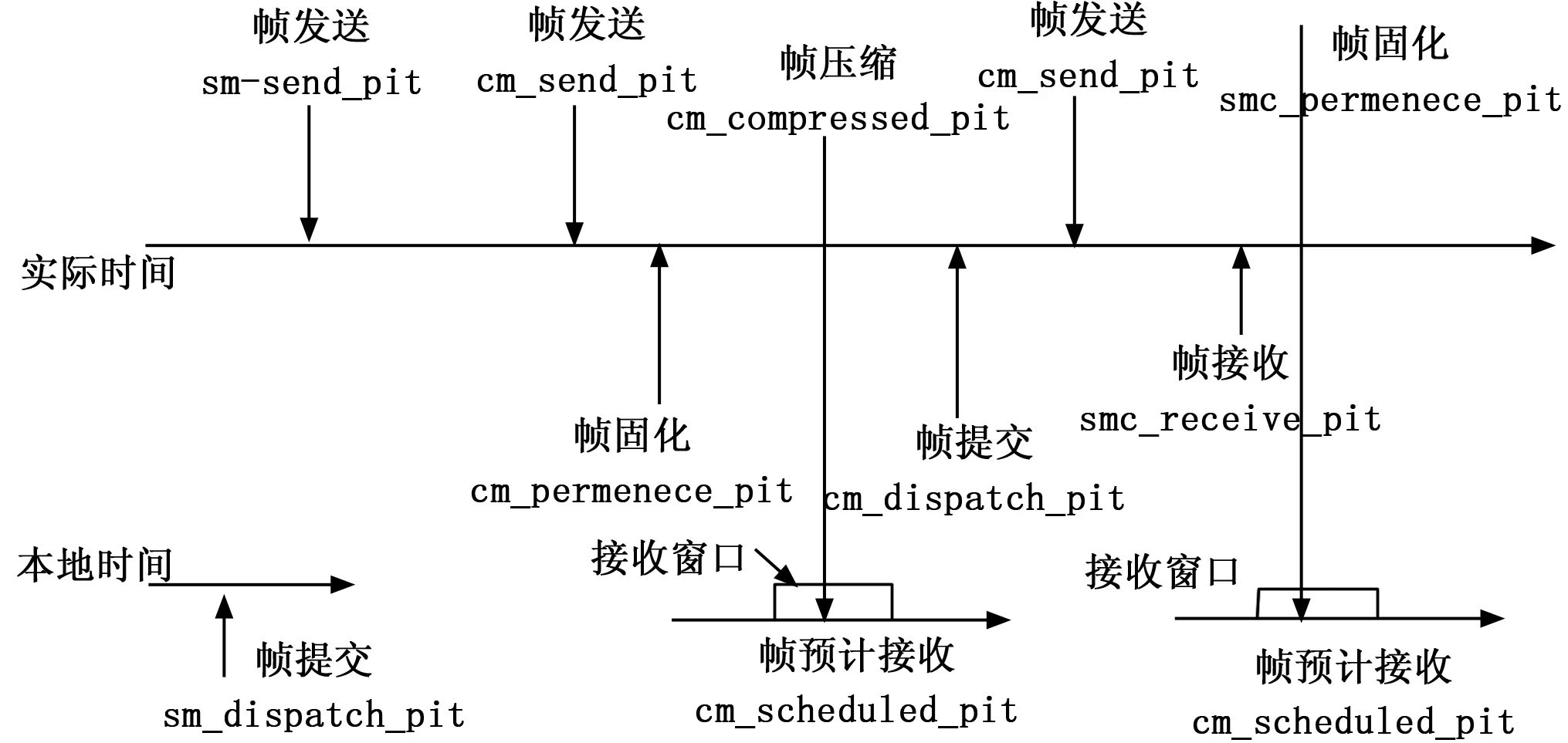
图1 TTE时钟同步过程

1.2 时钟同步精度影响因素

在深入分析TTE时钟同步的过程后，本文研究总结出影响TTE时间同步精度的3种主要因素，如图2所示。

图2 同步精度影响示意图

主要包括以下方面：

1)TTE时钟节点的栈内滞留时延抖动。操作系统及协议栈的滞留时延抖动影响TTE报文的收发时间戳标记的精确性，从而直接降低时钟同步精度。

2)透明时钟精确度。TTE时钟同步算法是基于透明时钟进行固化计算的，透明时钟的精确度是影响TTE时钟同步精度的关键之一，如果透明时钟记录的网络延迟与实际网络延迟越精确，那么透明时钟就越精确，同步算法计算出的时钟偏差就越准确，必然就会得到更高的时钟同步精度。

3)晶振稳定性。TTE时钟节点晶振的不稳定性因素也会降低同步精度。

1.2.1 TTE协议栈的滞留时延抖动

操作系统以及协议栈会带来时延抖动，TTE报文在经过协议栈时会进行封装和拆封报文的工作，这些过程带来的时延抖动也是不确定的，这样就会造成TTE报文时间戳标记不准确，进而降低时间同步精度。

通过分析，TTE时间戳标记的位置一般有以下几种：

1)应用层：采用在应用层socket接口处打时间戳的方式。传统的时间同步协议如NTP协议就采用软件方式在应用层加盖时间戳，受协议栈内滞留时延对时间戳的精确性影响较大，时间同步精度只能达到ms量级。

2)网卡驱动层： 采用在网卡驱动层打时间戳的方式是软件方式获得时间戳较好的位置。利用网络接口中断服务程序的入口处进行时间戳标记，操作系统的计时特性和负载决定了该方法的时间戳准确性。

3)MII接口处: MAC层和物理层之间的MII接口也称为媒体独立接口，在 MII接口处侦听捕获时间戳可获得较好的时间戳准确性。

4)物理层内，将硬件时间戳功能集成到PHY芯片中。

其中前两种为纯软件时间戳方式，成本较低，但精度不高。采用硬件方式打时间戳精度较高，能有效提高TTE时钟同步精度。

1.2.2 透明时钟精确度

透明时钟主要通过测量数据帧在设备以及链路上的驻留时间，并将其累加到对应的消息本身或跟随消息的修正域内。在时间触发以太网中，各节点将透明时钟的值累加、存储在PCF 的透明时钟域中，用来存储PCF 从源节点到目的节点经过的总时延。

透明时钟精确度主要包括三类延迟：节点发送延迟、中继延迟以及接收延迟。

其中三类延迟都与MAC层和PHY层对PCF帧的封装解析有关，具有较高的不确定性，此外还与本地时钟晶振稳定性、MAC和PHY芯片的性能和工作模式有关。而网络链路延迟是由物理介质属性决定的，延迟和不确定性都很小。

因此采用精确计算透明时钟的方法以及选用性能好且稳定的MAC和PHY芯片都能提高透明时钟的精确度。

1.2.3 晶振的不稳定性

晶振由于制造工艺的不同，本身就存在一定的频率偏差，加上环境因素的影响，频率偏差进一步加大。如果TTE时间节点选用这种频率偏差较大晶振那么在一段时间后相位偏差会变得很大，可能会影响网络正常工作，也是TTE不能容忍的。因此晶振的不稳定性也是影响时间同步精度的一个重要因素。

1.3 关键函数

1.3.1 固化函数

时间触发以太网通过时间固化实现了“延迟固化”功能。该算法的作用就是通过PCF 帧的到达时间确定该帧的发送时间。由于各个节点的时钟抖动以及网络参数等原因，使得PCF 帧之间的实际延迟存在不确定偏差，故采用时间固化函数来消除不确定偏差。

固化函数作用于CM、SM、SC所有节点，具体流程如下:

1)接收节点(CM/SM/SC)接收到PCF，读取本地时钟值记为1) 接收节点(CM/SC/SM)接收到PCF，读取本地时钟值记为receive_pit，并启动时间固化算法；

2)读取PCF的透明时钟域得到透明时钟值pcf_transparent_clock，即为PCF 在网络中传输的实际总延迟。

3)计算固化补偿延迟permanence_delay：

permanence_delay=max_transmission_delay- pcf_transparent_clock

(1)

4)计算固化时间点permanence_pit：

permanence_pit=receive_pit+permanence_delay

(2)

如上面算法，在接收端时间固化算法：

1)考虑了所有PCF 的时延得到整个通信网络的最大网络时延max_transmission_delay；

2)计算了时序保持时延permanence_delay。可将网络抖动造成的时延偏差转换到网络时延中。

在时序保持功能下：透明时钟机制可以提取网络抖动产生的时延；因为所有的PCF 帧到达目的节点后都是在permanence_pit时间点节点才认为该PCF 是有效可用的帧，故可以将所有PCF 的网络时延看作恒值max_transmission_delay。

1.3.2 压缩算法

TTE采用压缩算法实现网络节点间时间偏差均衡值的计算，用以时间同步。该算法通过CM整合同一个周期内SMs发来的IN帧固化时间点(permanence_pit)，通过调用压缩算法得到这些IN帧的均衡值(compression_pit)，并在等待一段时间后形成一个新的PCF帧广播到网络中其他SM和SC节点进行时间同步。

压缩函数由3个阶段组成：收集阶段、计算阶段和延迟阶段。

1)收集阶段。

当一个PCF帧固化之后并且当前没有相应集成周期处于激活状态的压缩函数正在收集PCF帧时，则从该时刻起开始压缩函数。压缩函数开始之后，开启第一个观察窗口(observation_window，OW)开始接受PCF帧。收集阶段遵循以下规则。(n代表当前OW，OWmax代表最大观察窗口)

(1)当n=1时，如果当前OW内收集到固化PCF帧小于2，那么停止收集，否则开启下一个OW。

(2)当n≥2,n≤OWmax时，如果当前OW没有收集到固化的PCF帧，那么停止收集，否则开启下一个OW。

(3)当n=OWmax,则该OW结束之后停止收集。

2)计算阶段。

该阶段根据收集阶段收集到的PCF固化时间点计算出压缩校验值(compression_correcion)input 表示在收集阶段的第i个PCF时间固化点和第一个PCF时间固化点的差值。

compression_correcion计算方法如下：(k表示所收集的PCF固化点数目，th+是顺次第f个，th-是倒次第f个)：

k=1:compression_correcion=input1;

k=2:compression_correcion=(input1+input2)/2;

k=3:compression_correcion=input2;

k=4:compression_correcion=(input2+input3)/2;

k=5:compression_correcion=(input2+input4)/2;

k>5:compression_correcion=(inputth++inputth-)/2;

(3)

3)延迟阶段。

该阶段在计算阶段之后延迟compression_correcion的时间得到压缩时间点(cm_compressed_pit)。在压缩时间点到来的时刻，新的PCF帧需准备好。

2 时钟噪声模型

TTE时钟同步过程由于采用了PCF帧交换的方式，这样将无法避免的带来时延抖动，其中主要存在协议栈时延抖动、物理层、硬MAC层等时延抖动。采用在链路层打时间戳的方式可以减少协议栈带的时延抖动，但是仍存在驱动中断、物理层以及硬MAC层等时延抖动[10]，并且各种延迟带来的抖动均为随机不确定的。本文中假设这些延迟抖动满足高斯正态分布,主要原因有：

1)文献[3]在Mica2Dot平台上，采用中断的方式在发送与接收首帧数据时记录时间戳。通过实验证明了时钟的频率偏移和时钟同步过程中的噪声均满足高斯分布。

2)存在于硬件电路中的随机噪声主要为热噪声,满足高斯分布。

3)相互独立的随机抖动根据中心极限定律叠加之后趋近于高斯分布。

时钟的状态行为通常可以用两种模型来表述, 一种是确定性模型, 另一种是随机模型。其中，确定性时间模型一般利用实际观测到的时间数据采用多项式拟合得到[8]。而随机模型则通常采用随机差分方程表示，其主要受频率偏移、过程噪声等的影响。

(4)

相应的两状态时钟模型用下面两个差分等式表示：

α(t+τ)=α(t)+β(t)·τ+ωα(t)

(5)

β(t+τ)=β(t)+ωβ(t)

(6)

其中:α(t)是相位偏差，β(t)是频率偏差，ωα(t)是调频白噪声，ωβ(t)是调频随机游走噪声。

3 时钟补偿算法

时间同步节点的本地时钟依靠其内部晶振实现，节点内部的计数器通过捕获晶振脉冲进行累加，完成对时间的计数。由于晶振本身的频率误差，启动时间不可能完全同步以及节点工作环境的影响，随着时间的流逝，不同节点间会出现一定的时间偏差。

节点时钟模型[11]是对时间同步协议性能进行有效分析的数学理论基础。由于节点晶振频率的不稳定性，通常节点i在某个t时刻的本地时间可以表示为公式(7)[12]：

(7)

其中:f0为节点晶振的标准频率，它是表征晶体物理特性的常量，fi(t)表示节点在时刻t的频率。通常由于制造工艺不同，fi(t)和f0存在微小差别。t0表示节点的初始时间，Ci(t0)表示节点在t0时刻的本地时间。

如果不考虑节点晶振频率变化以及外界环境影响，即认为在一定时间内节点晶振频率是保持不变的，那么节点的时钟可以表示为公式(8) :

(8)

其中:k=fi/f0为相对频率，Ci(t0)为节点在t0时刻的本地时间，在理想情况下，时间变化速率r(t)=dc(t)/dt=1，然而，在实际应用中，外界环境影响和晶振本身的频率变化导致公式(8)不能满足实际应用环境。但是晶振频率波动幅度也是有限度的，公式(9)可以描述这个变化幅度:

1-σ≤k≤1+σ

(9)

其中:σ为绝对频差上界，由制造厂商提供，取值范围通常在1～100 ppm，即节点在1 s内会有1～100 μs的时间偏移[9]。

3.1 线性渐进补偿算法

根据文献[6]，同步主节点SMk的时钟模型为:

C(t)_SMk=φk+αk(t)×t+nk(t)

(10)

其中:φk为相位偏差，αk(t)为时钟频率，nk(t)为随机噪声。

图3给出了参考时钟与本地时钟的关系，其中c1(t)表示本地时钟，它与参考时钟存在一个初始的相位偏差α(0)以及频率偏移β。c2(t)是只进行周期性相位偏移补偿后的同步时钟，由于不进行频率补偿，c2(t)与参考时钟一直存在β的频率偏移，在进行相位偏移补偿后，同步误差变小，但随着时间增大，同步误差会逐渐变大，最后呈现出锯齿状的特性。而c3(t)是只进行频率偏移补偿,它与参考时钟的频率接近，从c3(t)我们可以知道，如果本地时钟与参考时钟初始存在较小的相位偏移，并且保证本地时钟与参考时钟频率相近，那么就会得到较高的同步精度。

图3 时钟同步示意图

线性渐进补偿算法如图4所示：图中c1(t)与参考时钟的斜率偏移为β，斜率为1+β。假设K时刻c1(t)与参考时钟的相位偏移为α(k),如果采用直接补偿算法，那么补偿后的结果为c2(t),该时钟在K时刻出现了α(k)的跳变，此后仍保持原有的斜率。而c3(t)是采用线性渐进补偿算法之后的补偿结果,在调整期间，c3(t)将按指定频率进行调节，在剩下的同步间隔里，仍按原有的1+β斜率继续运行。

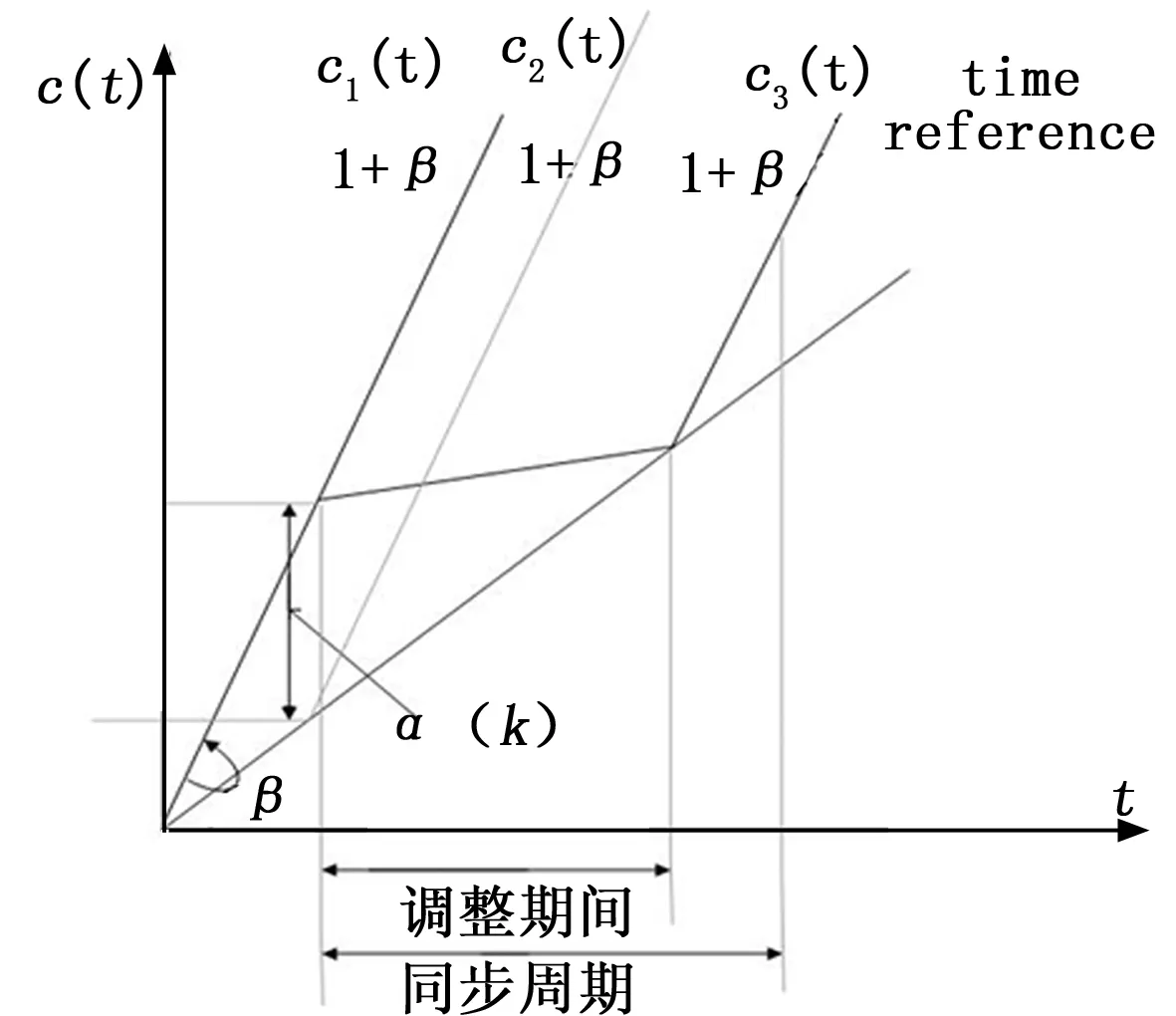
图4 线性渐进补偿算法

3.2 PI控制补偿算法

采用上文描述的线性渐进补偿算法调节相位偏差，虽然算法比较简单，但是实现精度不是很高，接下来介绍一种PI控制补偿算法分别对相位偏移以及频率偏移进行时钟补偿。

PI调节器是一种线性控制器，它根据给定值与实际输出值构成控制偏差，将偏差的比例和积分通过线性组合构成控制量，对被控对象进行控制。其控制方程为式(12):

(11)

其中:u(t)为PI控制器的输出,。e(t)为调节器的输入,Kp为比例系数,TI为积分时间常数。通常采用的PI控制器的离散形式如下：

(12)

其中:k=0,1,2……表示采样序列，Ts表示采样周期，Ki为积分系数。

控制器由比例和积分两个校正环节组成，各环节的作用如下：

比例调节作用：按比例反应系统的偏差，系统一旦出现了偏差，比例调节立即产生调节作用用以减少偏差。比例作用大，可以加快调节，减少误差,但是过大的比例，使系统的稳定性下降，甚至造成系统的不稳定。

积分调节作用：使系统消除稳态误差，提高无误差度。因为有误差，积分调节就进行直至无差，积分调节停止，积分调节输出一常值。积分作用的强弱取决于积分时间常数TI，TI越小，积分作用就越强。反之TI大则积分作用弱，加入积分调节可使系统稳定性下降，动态响应变慢。

PI数字调节器通常可以分为位置式控制器和增量式控制器。式(12)所示的就是位置式控制算法,控制器的输出直接调节被控对象。这种算法的优点是计算精度比较高,缺点是每次都要对e(k)进行累加，很容易出现积分饱和的情况，造成控制对象的不稳定，因此通常采用改进的抑制积分饱和的位置式控制算法，改进算法如下：

U(n)=Kp·e(n)+In(n-1)

In(n)=In(n-1)+Ki·e(n)+Ksat·epi

epi=Us-U(n)

(13)

其中:

当U(n)≥Umax时Us=Umax;

当U(n)≤Umax时Us=Umin

(14)

式中，Us表示抑制积分饱和算法的输出，U(n)表示本次PI调节器的计算结果，Ki表示积分系数，Kp表示积分系数，Ksat表示抗饱和系数，In(n)为本次积分累加和，Umax和Umin分别表示调节器输出的最大值和最小值，一般根据实际应用场景确定，本文中Umax和Umin可分别时间偏差offset的最大估计值和最小估计值。使用这种算法，可以将调节器的输出限定在需要的范围内，保证控制量不出现异常值。图5为抑制饱和位置式算法的流程图。

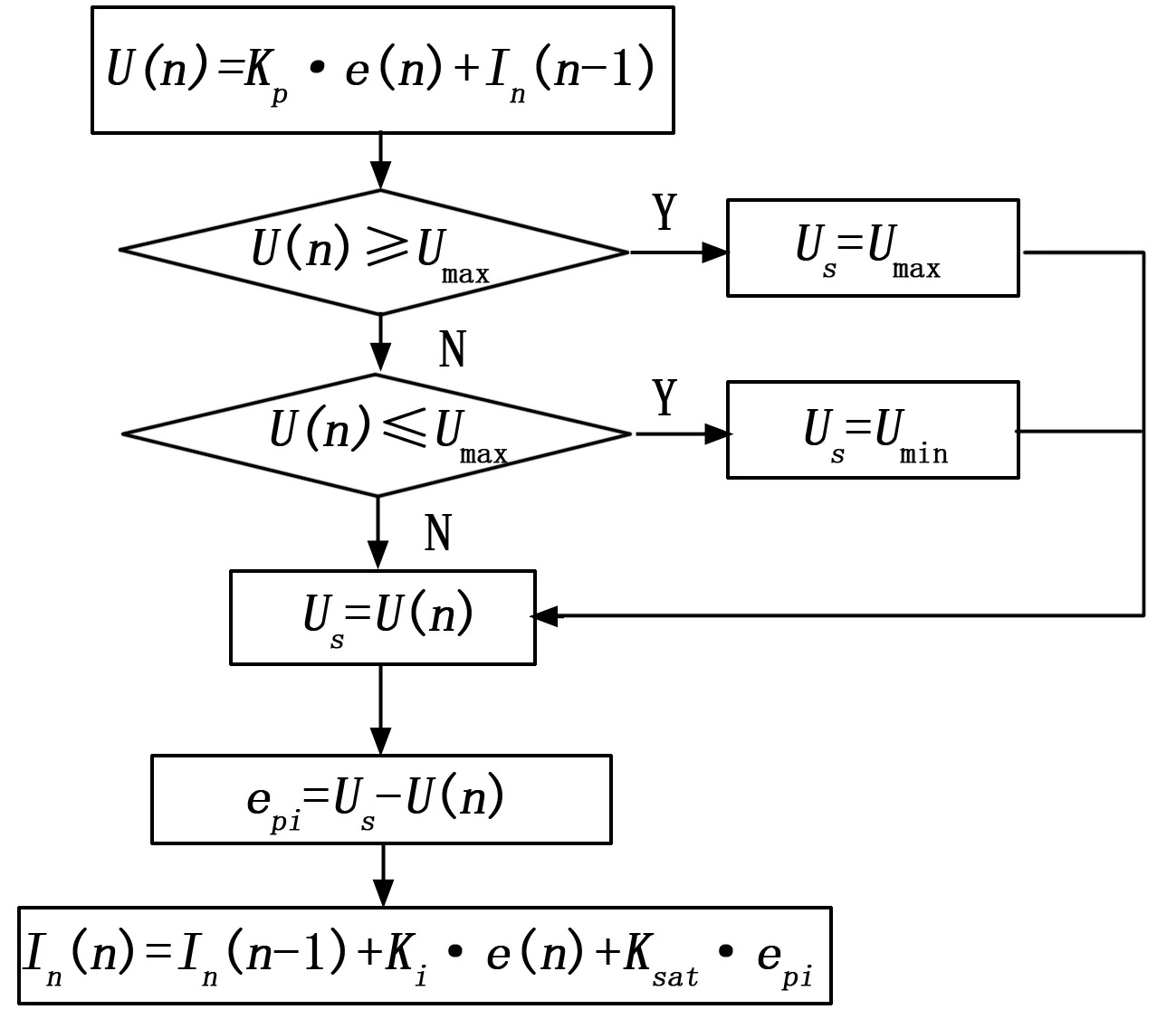
图5 抑制积分饱和的PI算法

图6为PI控制器相位偏移调整原理框图, 经过滤波算法的TTE时钟节点的相位偏移offset作为控制器的输入,利用PI控制器对本地时钟进行补偿。

图6 PI控制器的相位偏移调整原理图

由前面分析可知，如果只进行相位偏移补偿，那么时钟同步精度将与同步周期密切相关，如果能同时对相位偏移以及频率偏移进行补偿则能达到更好的效果。图7为时钟频率偏移补偿调整原理图,与相位偏移调整系统相比,增加了频率偏移估计器来计算频偏估计值。

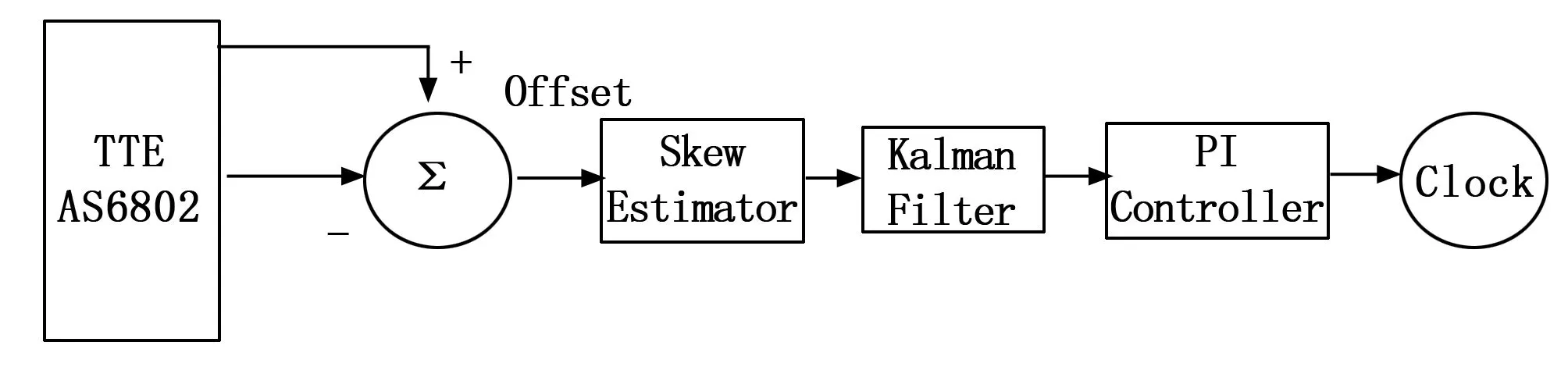
图7 PI控制器的频率偏移调整原理图

4 仿真分析

根据前面分析建立的时钟模型以及噪声模型，设初始相位偏差为100 ns,频率偏差为50 ppm，即节点1 s会出现50 μs的时间偏移[9]。由物理层抖动、链路抖动等带来的时间戳不确定性高斯噪声设为10-7。采样时间间隔为5 m，采样2 000个点即10 s，同步周期设为10 ms，时钟固有频率均为100 MHz，利用Matlab进行仿真。

如图8所示，相位偏移和频率偏移均叠加了高斯噪声,此外，相位偏移还受到频漂的影响。

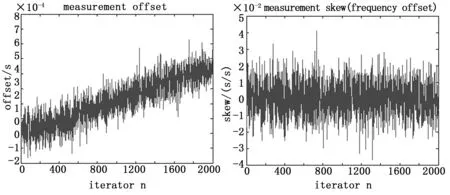
图8 具有高斯噪声的相位偏移和频率偏移

采用kalman滤波、自适应kalman滤波[7]以及均值滤波三种常见的滤波方法进行滤波得到的结果如图9所示：

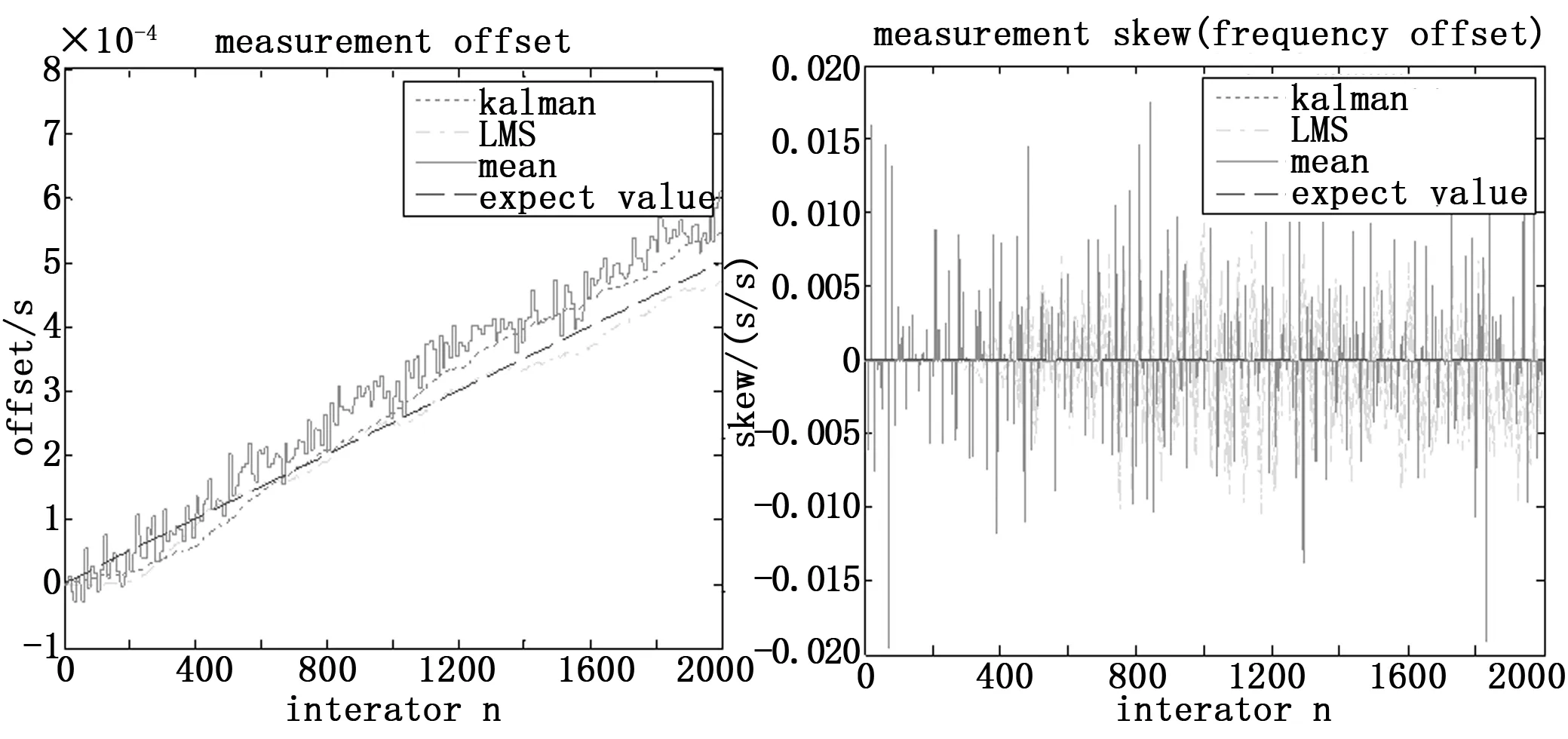
图9 滤波后的相位偏移和频率偏移

均值滤波方法算法简单容易实现，但相较于卡尔曼滤波以及LMS滤波方法效果更差，从图9可以看出kalman滤波方法具备更好的追踪性能。

线性渐进补偿算法的补偿结果如图10所示。

利用线性渐进补偿算法进行线性补偿后，相位偏移能达到亚微秒量级，但由于没进行频率偏移补偿，频率偏移仍然较大。

PI控制的补偿算法补偿结果如图11所示。

使用PI控制的补偿算法补偿之后，相位偏移达到了亚微妙量级，频率偏移也达到了良好的效果。

图10 线性渐进补偿结果

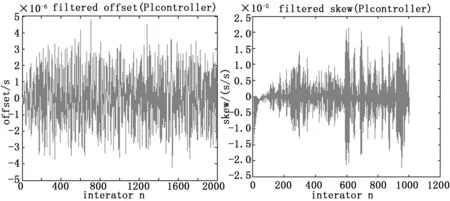
图11 PI控制器的补偿结果

5 结论

本文在深入分析TTE 时钟同步协议的基础上，总结了影响时间同步的因素，分析了时钟同步过程中存在的时间不确定性，建立了时钟噪声模型，根据噪声的统计特性采用了kalman滤波等三种滤波算法，得到了较好的效果。最后在滤除噪声的影响之后，采用了两种渐进时钟补偿方法对于时钟进行补偿，并通过仿真分析验证了算法的可行性。