适用于无向网络的动态Dijkstra算法优化
, ,
(1.军械工程学院 信息工程系,石家庄 050003; 2.军械工程学院 装备指挥与管理系,石家庄 050003)
0 引言
路由算法是网络研究中的关键问题[1-2]。为了减小数据在传输过程中的开销,通常寻找节点之间的最短路径。E.Dijkstra提出经典的最短路径算法[3],以一个节点为根,形成最短路径树(SPT,Shortest Path Tree),适用于寻找单节点到网络中任意节点的最短路径。在实际的网络中,网络的拓扑结构会因为各种原因发生改变,例如链路失效、节点宕机、新节点加入等。在网络模型中,拓扑结构的变化一般总结为以下4种情况:边的权值增大或减小、节点增加或删除[4-5]。当网络拓扑小范围发生变化时,通过Dijkstra算法从根节点开始重构SPT,能够解决这个问题。但是这种静态的算法重构SPT会造成大量不必要的开销,因为小范围拓扑发生变化,有许多节点在最短路径树中的位置是不发生改变的。
为了优化算法性能,提出了动态Dijkstra算法[6]。动态Dijkstra算法的核心思想是尽可能保持现有SPT的结构,缩小需要重新计算的节点的范围,降低更新SPT过程的复杂程度。文献[7]最早提出动态更新最短路径树算法(DSPT),但是算法所划定的更新范围仍有冗余。NSPT算法[8],Ball-and-String算法[9-10]是比较高效的动态算法,解决了有边的权重增大减小的状况。文献[11]提出了多条边发生变化时的解决方法。这些算法基于的网络模型大多是有向网络模型,但在实际计算机网络中,一般是数据正反向都能传递的无向网络。在无向网络模型中,两个节点只有连接关系而无先后顺序,因此在算法中无法利用节点先后连接参数。文献[12]提出了较为成熟动态算法的思想,讨论了在网络中一条边权值变化的SPT更新算法。但是该算法适用于有向网络模型,同时对于所处理的节点范围没有进行必要的筛选,还是有部分冗余计算。本文在此基础上提出了适用于无向网络的动态更新SPT算法,优化了受影响节点的筛选机制,进一步缩小了节点更新范围。
1 Dijkstra算法基本原理
Dijkstra算法是求单源最短路径的经典算法。它采用标记法按照路径长度递增的顺序寻找最短路径,首先从源点开始,找出长度最短的一条路径及节点,然后从新节点出发,通过迭代得到从源点到其余各节点的最短路径[13]。为了跟后来所研究的动态Dijkstra算法形成对应,把经典的Dijkstra算法称作静态Dijkstra算法。
Dijkstra算法的基本过程[14]如下:在整个网络中设置两个集合,集合T是经过计算加入到最短路径树中的节点,集合S是还未加入到最短路径树中的节点。假设每个节点vj都有一对参数(dj,pj),dj是从源节点vs到节点vj的最短路径长度,pj代表节点vj在最短路径中的父亲节点。
步骤一:初始化,T=φ,S包含了网络中的所有节点。设置所有节点dj=∞,pj=[.]
步骤二:将源节点vs加入集合T,并从S中删除,设置ds=0,ps∈φ。
步骤三:检验集合T中的所有节点vi到的S中节点vj的距离lij,其中vi到vj必须是直接连接的,中间无其他节点。设置dj=min[dj,di+lij]。
步骤四:选取dj最小的节点vj,将其从集合S中删除,并加入到集合T中去,该节点成为最短路径树中的一个新节点。
步骤五:找到新节点vj的父亲节点pj,并记录该节点的两个参数(dj,pj)。
步骤六:重复步骤三到步骤五的过程,直到网络中的所有节点全部加入到集合T中,此时集合S=φ,完成整个过程。
2 算法设计
2.1 参量设置
假设存在加权无向网络G=(V,E),V表示节点的集合,E表示边的集合,|V|=n,|E|=m。G中的节点用v来表示,用下标加以区分。e代表两个有直接连接的节点之间的边,权值用w(e)表示。从根节点的整个网络的最短路径树表示为SPT(Shortest Path Tree),d(v)表示从根节点到节点v的最短路径长度,p(v)表示节点v的在SPT中的父亲节点,T(v)表示在SPT中以v为根节点的子最短路径树的节点的集合。对网络中的所有节点设置一个状态参量Sta(v),当Sta(v)=1表示节点v在SPT′(更新后的SPT)中的位置已经固定,不再需要处理;Sta(v)=0表示节点的位置仍需要更新。设置一个集合Q,存储等待处理的节点及节点d(v)的变化量。该算法讨论的是无向网路,必要时用[vi,vj]来表示两个节点及所形成的边。vi、vj的先后顺序与表示的结果无关,也就是说[vi,vj]和[vj,vi]实际上表示的是同一条边。相比于有向网络,无向网络需要解决的问题更复杂一些。
2.2 算法描述
假设在网络G中,关于根节点vs的SPT已经构造完成。当检测到有一条边e0的权值发生变化时,需要首先确定SPT受影响的范围[15]。算法是分成权值增大和权值减小两种情况进行处理的。
情况一:权值增大时。如果权值增大的边不是SPT中的边(例如图1中的[v5,v6]),由于各节点的最短路径长度(d值)已经是当前最小的,非SPT中的边权值增大不会改变各节点到根节点的d值,因此这种情况下不会影响SPT结构。如果SPT中的一条边的权值增大,假设图1中,边[v2,v6]的权值由3变为10,增加了7,这将导致以v6为根节点的子树(T(v6))中的节点到vs的距离都会增加,此时在网络中的位置不一定是路径最短的位置,因此需要对这些节点的位置进行调整。边[v2,v6]权值增加后影响到的节点范围在图中用虚线圈出。将T(v6)中的节点的d值全都增加7,并把它们的Sta(v)参数置为0,表示节点位置等待更新;原SPT中的其他节点Sta(v)置为1,表示节点位置已经固定。
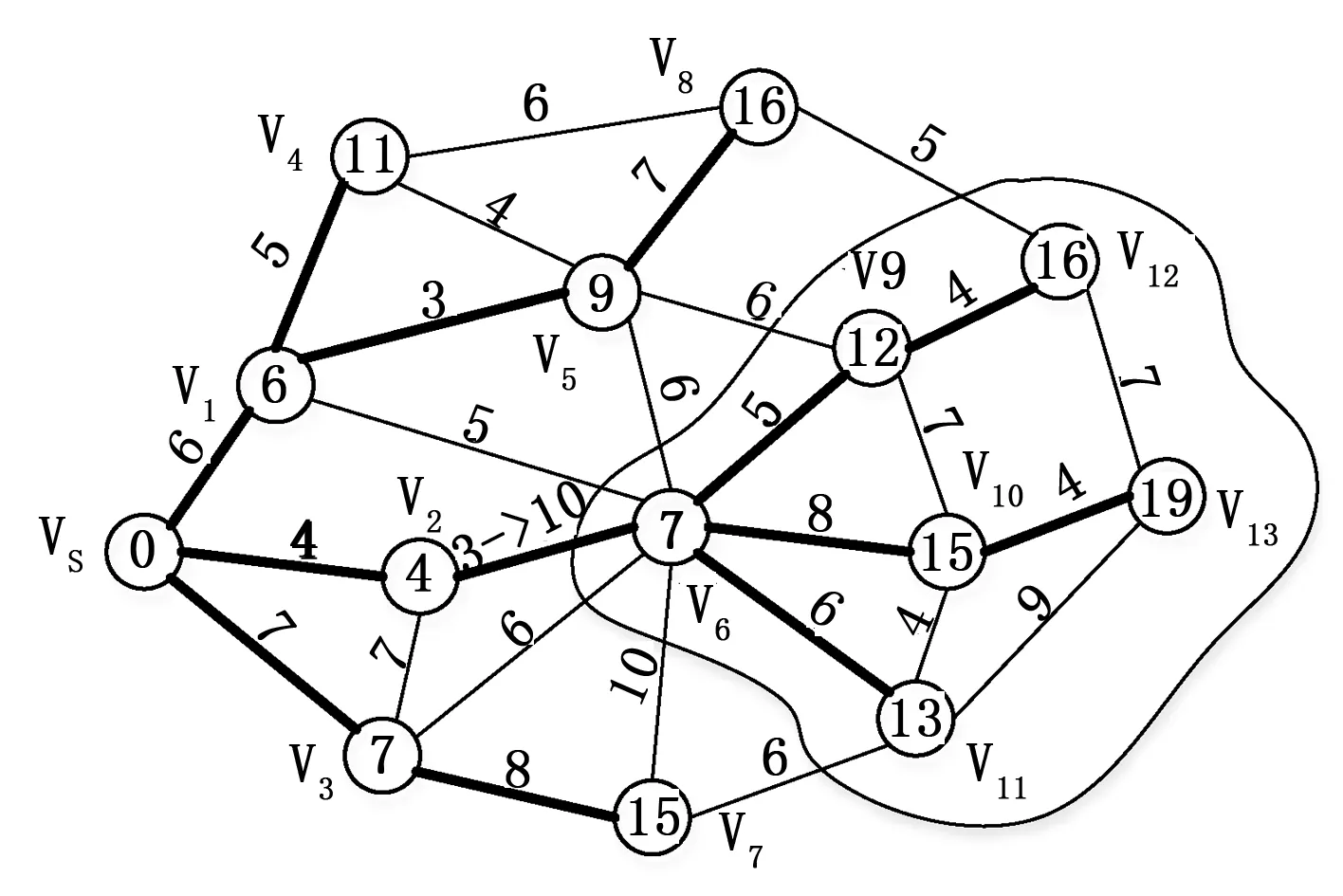
图1 使用Dijkstra算法计算的最短路径树
所有与待更新节点相连的节点都有可能成为新的父亲节点,在文献[12]的算法中,把所有的连接边都纳入到了判断范围之内,但实际仍有部分是无需考虑的。与待更新节点相连的边有三种类型,以v9为例:(a)与T(v6)之外的节点相连的边,例如[v5,v9];(b)与T(v6)内节点相连但不属于T(v6)的边,例如[v10,v9];(c)与T(v6)内节点相连但且属于T(v6)的边,例如[v6,v9][v9,v12]。其中c类边不纳入考虑范围是显然的;b类边,两个节点的d值加上了相同的增量,不会改变待更新节点的父亲节点;只有a类边存在改变待更新节点最短路径的可能。因此在下一步操作之前可以首先把b、c类边排除,达到缩减计算范围的目的。该部分判定过程对应于算法1中的第8行伪代码。在a类边中,计算边的对应节点的最短路径值与该边权值之和,如果小于待更新节点的最短路径值,则将这个待更新节点以及对应的边、节点加入到集合Q中,并将这个差值δ(vj)=d(vi)+w(e)-d(vj)记录下来。表1显示了图1中首先加入到Q中的项。
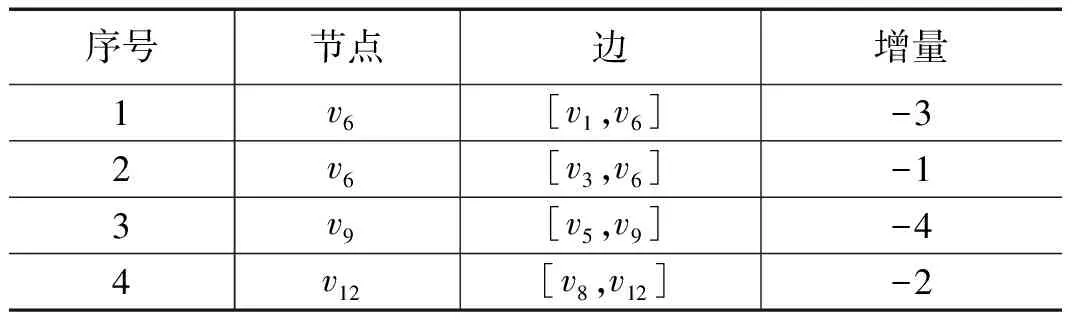
表1 父亲节点可能改变的节点及对应边和增量
从集合Q中选取δ(vj)最小的一组数据,对应的边的另一个节点vi就是该节点vj的新父亲节点。将以vj为根节点子树中的所有节点的最短路径值加上该增量值(负值),状态参量修改为1,删除集合Q中所有跟这些节点有关的项。
定理1:跟随vj加入到新SPT中的T(vi)子树中的节点,处于当前的最短路径。
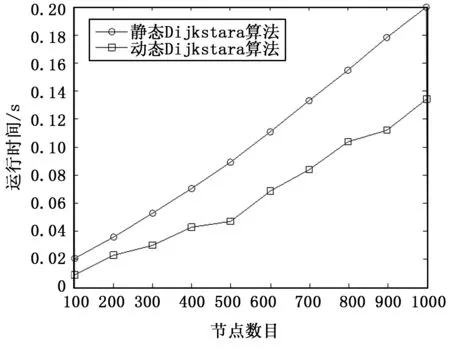
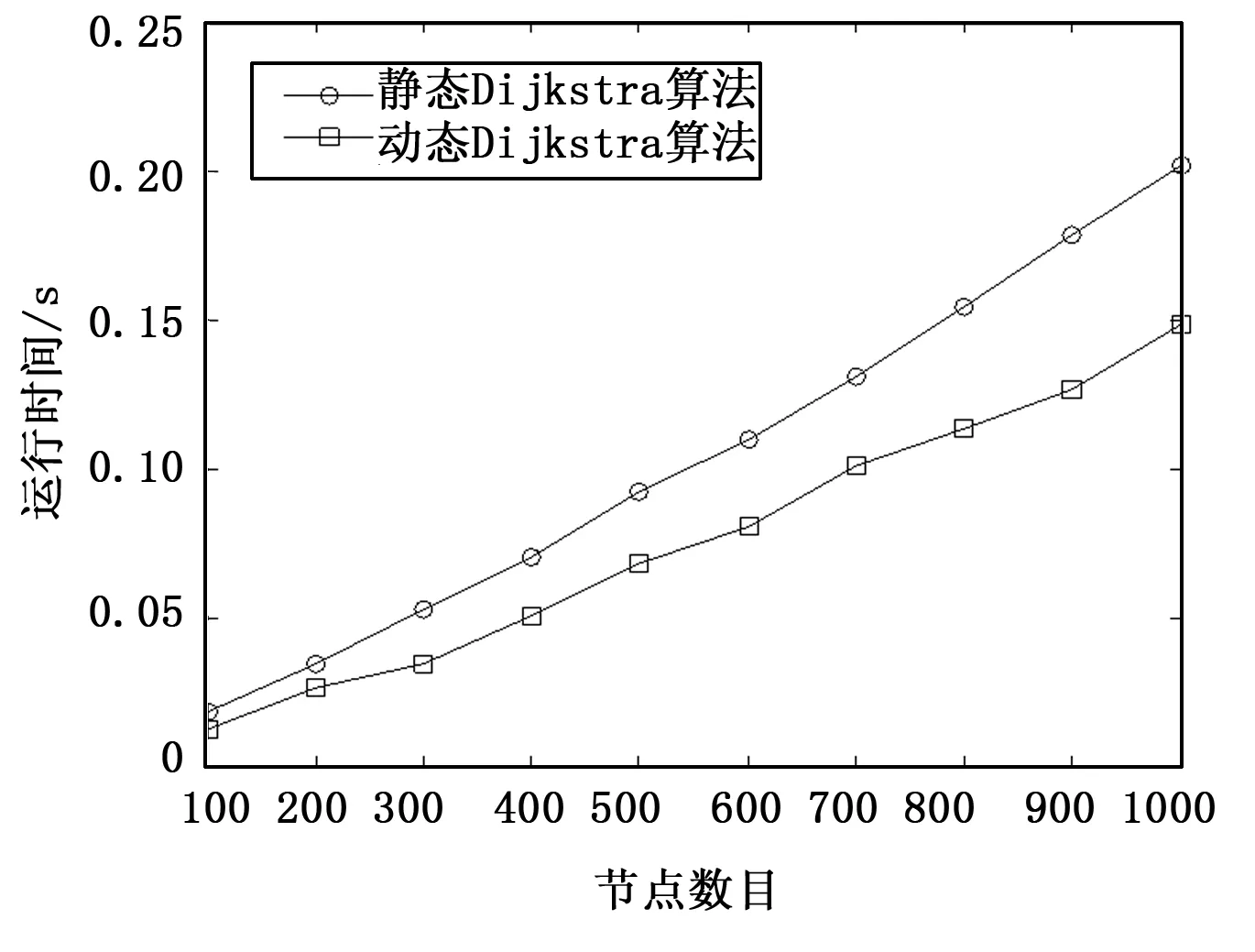
证明1:对T(vj)中的任意节点vt,假设存在vx使得d(vx)+w([vx,vt]) 图2 使用动态Dijkstra算法更新后的树 由于更新节点最短路径值d的减小,会使与之相连的节点的父亲节点发生改变,因此需要将d(vi)+w(e)-d(vj)<0的节点对应的项加入到集合Q中去,重复更新过程。直到Q变成空集为止,退出循环,整个更新过程结束。该部分算法的伪码描述见算法1,更新之后的SPT如图2所示。 算法1:权值增大的SPT更新算法。Input:网络G,根节点vs,边e的权值从w(e)变为w′(e);Output:以vs为根节点的新SPT′1)Initialize SPT from G2)wait until one edge e0=[vi,vj]:w(e0)→w′(e0)3)if w′(e0)-w(e0)>0,then4)if e0∉E(SPT) 不处理 //不是SPT上的边无影响,不处理5)else if e0∈E(SPT)6)初始化. δ=w′(e0)-w(e0);∀v∈V(SPT)设置为Sta(v)=1; 若vi=p(vj),∀v∈T(vj),d(v)=d(v)+δ,Sta(v)=07)end8)for all e=[vi,vj]∧Sta(vi)=1∧Sta(vj)=0 do9)if δ(vj)=d(vi)+w(e)-d(vj)<0 then10)add {vi,vj,δ(vj)} to Q11)end if12)end for13)end if14)while Q≠ϕ15){vi,vj,δ(vj)}←minQ,修改p(vj)=vi16)for all v∈T(vj) do17)修改d(v)=d(v)+δ(vj),Sta(v)=1,delete ∀v∈T(vj) from Q18)end for19)for all e=[vi,vj]∧Sta(vi)=1∧Sta(vj)=0 do20)if δ(vj)=d(vi)+w(e)-d(vj)<0 and {vi,vj,δ(vj)}∉Q do21)add {vi,vj,δ(vj)} to Q22)end if23)end for24)end while 情况二:权值减小时。与情况一类似,权值减小的边出现的情况有两种,或不属于SPT中的边,或属于SPT中的边。这两种情况都有可能造成SPT结构的变化,因此边的权值减小受到影响节点的情况相对更复杂。 对于不属于SPT中的边权值减小,首先比较这条边对应的两个节点最短路径值的大小,d值比较小的节点可能成为比较大的节点的新父亲节点。具体能否构成此影响,还要看“准父亲节点”的d值与边的新权值之和跟另一个节点d值的大小关系。如果“准父亲节点”的d值与边的新权值之和比较小,则修改另一个节点的父亲节点,以此节点为根的子树中的节点是此次受到影响的范围;如果“准父亲节点”的d值与边的新权值之和比较大,那么此次权值的变更对SPT没有影响。 对于属于SPT中的边权值减小,需要首先判断这条边的两个节点在树中的父子关系,找到子节点,以子节点为根的子树中的节点到根节点的最短距离d会因此变得更小,因此这仍是SPT的一部分。网络中的其他节点的最短路径会有一种向这部分节点“聚集”的趋势,因此剩下的节点即是此次权值变更受到影响的节点范围。算法的其他处理过程与情况一类似,在这里不再过多描述。该部分算法的初始化部分的伪码描述见算法2。 算法2:权值减小的SPT更新算法。1) /∗w′(e0)-w(e0)<0∗/2)if e0∉E(SPT)3)若d(vi) 为了验证算法的正确性,本节进行实验验证。实验运行主机配置为:CPU主频3.20 GHz,内存大小为4 GB,操做系统为Windows 7旗舰版。设置网络节点数为N的无向网络,N取[100,1000],步长值为100。赋予网络连接边以及边的权值,设置节点的平均度为5,权值范围为[20,80]。首先根据生成的网络计算出SPT,随机选择一条边的改变权值,考查静态Dijkstra算法和本文提出的动态 Dijkstra算法在更新SPT所需要的时间。鉴于当权值增大和权值减小时算法的处理过程有所差异,所以在实验中也分两种情况分别进行比较。实验结果如图3图4所示。 图3显示了当一条边的权值增大时,在不同网络规模下,静态Dijkstra算法和动态Dijkstra算法更新SPT所需要的时间;图4显示了当一条边的权值减小时,在不同网络规模下,静态Dijkstra算法和动态Dijkstra算法更新SPT所需要的时间。两种情况下动态算法都比静态算法的时间开销要小,能在相对短的时间内更新SPT,体现出了更好的性能。结合图3图4来看,在节点数目相同时,权值增大和减小静态Dijkstra算法更新SPT所用的时间几乎一样,这是因为当检测到有边的权值发生变化时,静态Dijkstra算法都是从根节点开始更新SPT;两种情况下动态Dijkstra算法的变化趋势几乎一样,因为两部分算法的时间复杂度比较接近。 图3 权值增大时更新SPT的时间与节点数的关系 图4 权值减小时更新SPT的时间与节点数的关系 当网络节点或边发生变动时,动态路由算法尽可能地对已有的最短路径树做最小改动来保持SPT 的稳定,节省了计算时间,比静态算法更具有优势。本文提出了适用于无向网络的Dijkstra动态算法,并对算法中节点的更新范围作了进一步优化,证明了改进的合理性。最后通过实验,比较了当网络中的一条边的权值变化时,动态算法和静态算法更新SPT所需的时间,验证了所提出算法的可行性和优越性。文章只提出了边的权值发生变化的有关算法,在下一步研究中,将对节点增删以及多边、多节点变化的情况进行讨论,并进一步通过实验来验证所得出的结论。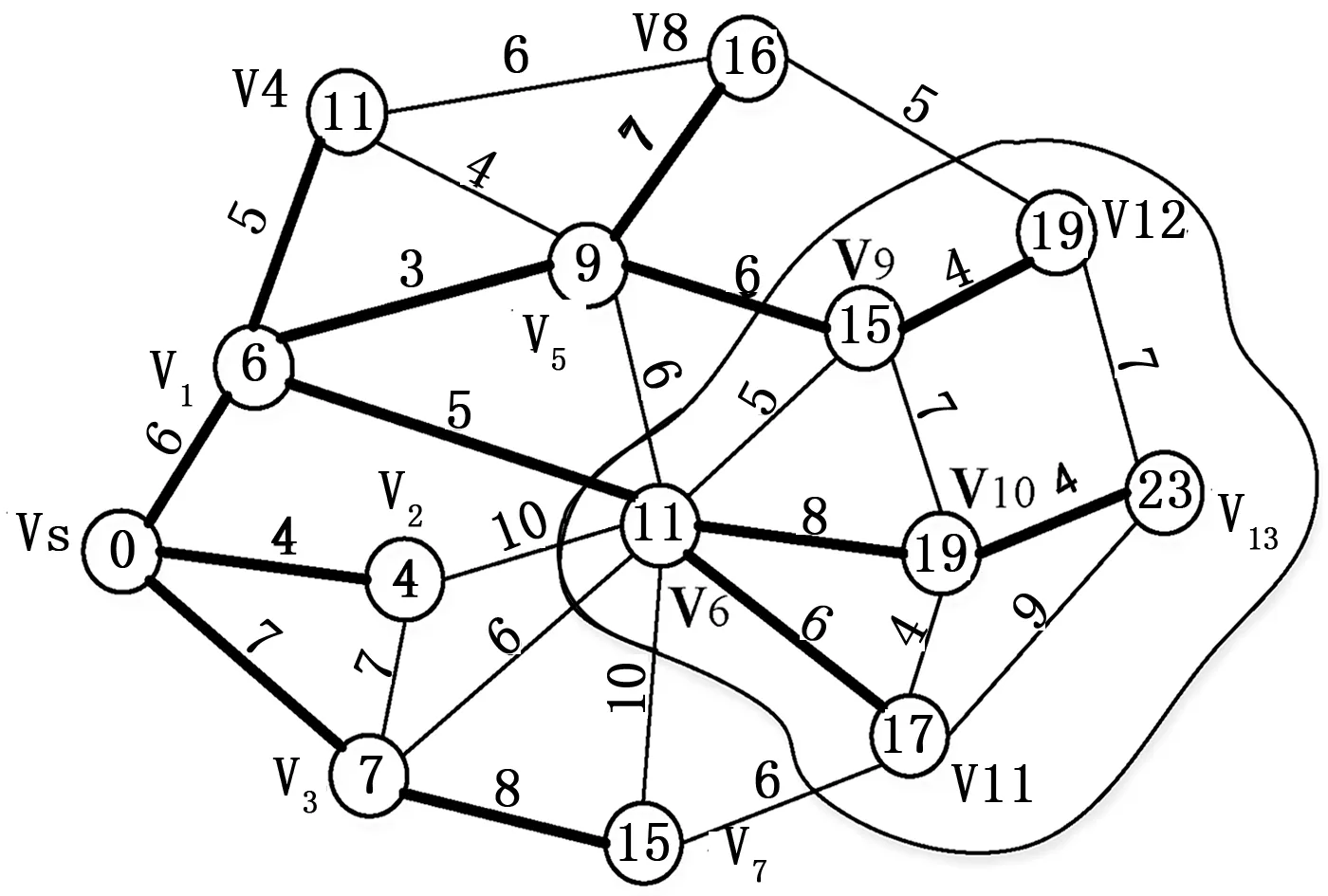


3 实验验证与分析
4 结束语

