基于数学模型分析的小提琴谐音能量分布特性研究

杨 波，李圣辰，韩宝强

(1.中国音乐学院 音乐科技系，北京 100101； 2.北京邮电大学 信息光子学与光通信研究院，北京 100876)

小提琴琴弦振动产生的声音是复合音，其中包含整弦振动和部分弦振动的声音，整弦振动产生基音，部分振动产生泛音，基音和泛音统称为谐音.其中，基音为1号谐音，第一泛音为2号谐音……以此类推.谐音的分布情况，是一件乐器所发出声音的质量一个的重要参考方面[1].研究谐音，对于研究乐器的音色有十分重要的作用[2]，例如人耳可以根据谐音的不同来识别乐器或者是人声.因此，研究乐器谐音的数量、能量以及分布，对于调查乐器的质量、声音的音色以及指导乐器的制造等方面，有积极的作用.

传统分析乐器谐音的方法，多通过不同的硬件如频谱分析仪，或者软件如GMAS通用音乐分析系统来完成，其分析对象一般以一个音为单位.这样的分析方法不利于大规模进行研究，且受到样本的是否具有典型性、样本的稳定性等因素的影响，其结果仅针对单个被研究样本.本文研究对象为3个八度音阶的音，从频谱分析的结果数据中，提取谐音能量数据进行数学建模.这种方法较传统方法更具有样本的概括性，得到的结果也更稳定，减少了样本是否具有典型性等偶然因素的影响.在已有的研究中，缺乏使用数学方法对小提琴谐音分布规律的研究工作，所以本文拟使用数学建模的方法对不同小提琴的谐音能量分布规律进行比较研究.一般来说，物理模型的分析方法是基于相关抽象假设的，本文的方法是由实际情况出发，研究小提琴谐音在能量分布上的结果，进行建模和对比，因此本文方法不受相关假设的影响.

本文使用自行录制的6把小提琴音阶音频作为数据库来源，样本音频包括g到g3的22个音(G大调).小提琴音域大致为g到c4，本实验所用样本选择的22个音，基本涵盖了小提琴音域内的音，因此样本具有一定的代表性.实验过程首先使用常数Q变换(Constant-Q Transform, CQT)对每一个音进行频谱分析，通过寻找基音和谐音，提取有效的谐音及能量分布.借助高斯混合模型根据每把小提琴22个音的谐音及能量特性为每把小提琴的谐音进行数学建模，然后使用Kullback-Leibler(KL)散度对得到的6把小提琴的数学模型进行两两对比，研究数据间的差异性.最后借助假设验证完成所有琴差异的统计，研究在不同频域范围内谐音分布规律的差异是否显著，得出小提琴不同谐音间差异性的大小，即具有显著差异的谐音和不具有显著差异的谐音分别有哪些.

实验结果显示，在调查的小提琴前12号谐音中，根据谐音能量分布规律间差异的显著性，可以分为3个层次： 首先，5号、9号、11号谐音具有的差异显著性最低；其次，3号、4号、7号、8号、10号谐音的差异显著性中等；最后，2号、6号和12号谐音的差异显著性最大.实验说明本文提出为小提琴谐音能量分布建模进行研究是有效的.此结果可以被用来对比研究乐器音色、研究乐器质量，或者乐器识别等方面.

1 研究现状及相关研究

在对乐器进行声学研究方面，小提琴声学一直是被热切关注的焦点.Von Helmholtz在《On the Sensations of Tone as a Physiological Basis for the Theory of Music》[1]中，对小提琴及弦乐器有一定的研究.这本书比较详细地介绍了音乐声学的相关知识，对于我们进行音乐声音音频分析的研究具有指导的意义.同时，在该书中，作者介绍了谐音是乐器声音品质的一个重要方面，并提出谐音对于乐器音色有重要影响.

《The Science of Sound》[3]亦是一本关于乐器和乐器声音研究的书，作者提出乐器的音色不仅受谐音的影响，还受到频谱包络和持续等因素的影响，但谐音是更为重要的方面.该书中，第三章节介绍了小提琴声学，主要集中在弦振动、琴体振动以及空腔振动等方面.该研究是从小提琴本身振动出发的，本文则通过分析小提琴音频的频谱数据分布情况，并进行数学建模，以提供更加实际的分析结果.

研究乐器的谐音，首先需要进行频谱分析.CQT[4]被证明在频谱分析和频谱信息提取方面是非常有效的.文献[4]提出使用中心频率和带宽的恒定比值(Q值)，以及按照几何级数展开的频率轴，来完成快速傅里叶变换.本文选择此方法来提取每一个音的频谱信息.

我们参考了一些对乐器音频进行分析的文献.文献[5]介绍了几种分析音频的方法，比较笼统.文献[6]介绍了利用插值法进行短时频谱分析.本文提出的研究创新点在于利用数理统计的方法，对音频频谱分析结果进行研究，得到谐音的能量分布规律.同时频谱分析不是本文的重点，且不作深入讨论.另外在参考的文献中找到一些研究乐器谐音不同侧重点的文章.如文献[7-8]研究谐音的共振峰；文献[9]提出借助适应基音的多框架集合分析方法，提取频谱包络；文献[10]侧重在捕捉频谱包络的变化.在参考的研究中，首先注意到，研究乐器的谐音是非常重要且有意义的，可以从多方面、多角度对乐器的谐音进行调查研究.而本文的方法是利用统计方法来研究乐器谐音能量分布，这在已有的研究中是鲜有的，因此是本文的创新点.在计算方面，我们主要通过MATLAB来完成，并参考了文献[11]中使用MATLAB进行声音分析的方法.

2 数据库

依据本文所提出的研究小提琴谐音分布模型的方法，需要自行录制所需音频.其原因主要有两点： 第一，在已有的音频数据库中，小提琴音频数量有限，不能够满足本实验的需求；第二，实验中需要尽量避免除小提琴以外的其他因素的影响，例如演奏者、录音环境、录音设备等.因此，本文所使用的小提琴音频，是作者自行录制的，并保证演奏员、录音环境、设备等都是相同的.

用于实验的样本音频是来自6把中国制造、价格相近且相近生产时间的小提琴，这些琴从生产后一直在使用中.我们要求一位演奏员(余彦男，宁波交响乐团小提琴演奏家)，在每一把小提琴上演奏3个八度的G大调音阶，也就是每把琴22个音，将这些音作为得到这把琴最终用于比较的数据的样本来源.每把琴演奏上行音阶两遍，每个音以每分钟60拍的速度演奏4拍，音与音之间间隔2拍，也就是每个音长度约为4s.待录音结束，由演奏员亲自试听，从两遍中选择一遍作为最终样本来源，试听内容主要参考音准、强度和稳定度.

录音使用具有强指向性的SCHOPES MK4麦克风，这个麦克风具有较强的指向性，因此可以减少环境噪音对录音的影响.录音软件使用Digidesign公司的ProTools，录音完成后未对音频做后期处理.录音时令麦克风指向小提琴f孔，距离为1m，并确保演奏员和麦克风的位置固定，这样可以更好地拾取直达声，且尽量减少环境因素的影响.最终音频的采样率为96kHz，采样精度为24bit.根据尼奎斯特采样定理，本样本采样率所容纳的信号中最大频率分量频率为48kHz，是超过人耳可听阈的，符合本实验的要求.样本的录音地点是在中国音乐学院国音堂地下录音棚.所有样本音频是在同一天同一地点且由同一位演奏员演奏的，尽可能移除了可能存在的变量，如演奏员身体状况、录音棚环境状况等，保证录音的统一性，以进行比较研究.

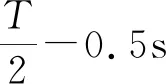
3 实验过程

我们使用A(f,t)来代表频谱分析的结果，意为某一时刻、某一频率的振幅.我们知道，在某一频率下，不同时刻的振幅是不稳定的.所以需要计算振幅在某一频率下，所有时刻的平均值，以此来去掉不稳定性.计算公式如下：

(1)

式中：t0是窗长，为1024；fs是采样率，为96kHz.

图1 数据裁剪示意图Fig.1 Example of data frame

于是，我们得到了每个音在不同频率段下的振幅值.本文着重考虑的是小提琴的谐音，因此，根据已知音的音高(基音频率)，去除基音频率以下的数据.随着音高的不断升高，基音的频率也在升高.这就导致经过去掉基音以下部分后，剩下的数据结构长度不一致，音高越高，数据长度越短.为了保证每一个数据的长度一致，需要按照最高音的数据长度来裁剪其他音的数据，如图1所示.

到此为止，我们得到了每一个经过处理后的数据，每把琴有22个这样的数据.每一行数据的第一个元素为这个音的基音振幅.因为每一个音的基音频率并不是一样的，所以需要进行标准化，即令基音频率为1，其余各谐音需计算其频率与基音频率的比值，即：

(2)

根据之前频谱分析时将每一个八度分成n(n=120)个单位，所以我们可以通过式(3)来计算频率比值：

(3)

基于同样的原因，为了使振幅之间具有可比性，我们需要将振幅也作标准化处理.将基音的振幅设为1，其他频率的振幅依次计算其与基音振幅的比值，即：

(4)

琴弦整弦振动产生基音，2次谐音频率是基音的2倍，3次谐音是基音的3倍……[2]因此，我们尝试将每把琴的22个音的数据求平均值，能够简化并得到这把琴每个谐音振幅与基音振幅的比值的平均水平，即：

(5)

式中：n为22，即22个音；i为每个音的编号；k为频率比值点序号.

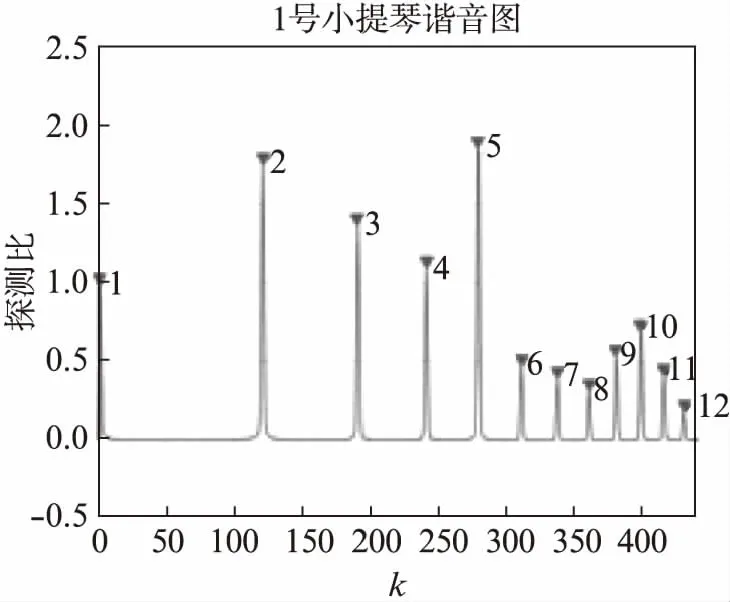
图2 寻找谐音位置示意图Fig.2 Example of finding harmonics location

接下来，我们使用寻找峰值的办法，找到每一个谐音的所在位置.谐音的定义要满足：

(6)

其中，因为非谐音成分占数据中的大多数且其幅值比较小，所以我们将阈值设为该琴数据的平均值，从而找到谐音的所在位置.将1号小提琴的谐音示意图展示如图2所示.

从图中我们可以清楚地找到本实验中小提琴的谐音，包括基音在内共12个谐音.现将所有琴的除基音外的谐音位置数据整理如表1所示.

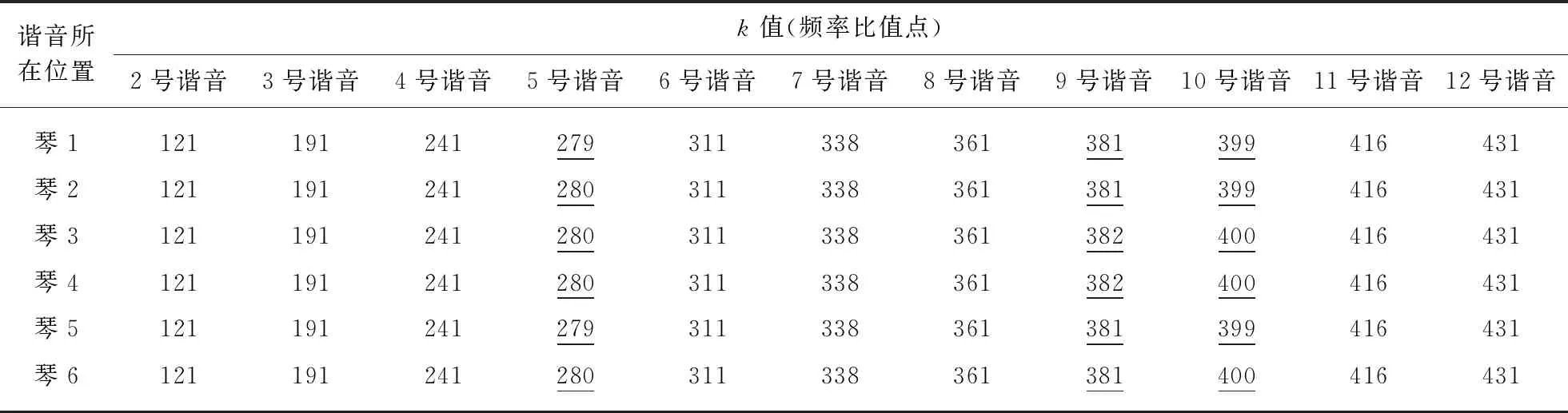
表1 谐音位置表

从表1中我们看到，小提琴谐音与基音频率比值并不完全一致.在5号谐音、9号谐音和10号谐音处(表1中划线的数据)，谐音频率比不统一，但差距不是非常的大.根据式(3)，可以计算各谐音与基音频率的比值.1，5，6号琴的第5号谐音与基音的比值为5.0101，其余3把琴的比值为5.0397；3，4号琴的第9号谐音与基音的比值为9.0840，其余4把琴的比值为9.0317；1，2，5号琴的第10号谐音与基音的比值为10.0213，其余3把琴的比值为10.0794.猜想其原因可能与琴弦的质量有关，误差可忽略.

在实验中，除了之前发现的3个谐音频率比有差异，其余谐音的频率比是相同的.本文的目的是研究频域内谐音能量的分布规律，所以我们将每个琴的谐音数据进行整理，将不统一处的谐音位置进行调换，使之与其他琴的谐音位置统一，再继续进行深入谐音分布规律的探究.我们使用高斯混合模型将振幅比值按照各频率比值点进行分布规律统计，即：

(7)

然后对每一把琴的各频率比值点上的振幅比值分布进行统计，即：

(8)

式中i代表琴的编号.

接下来，使用上一步得到的结果，使用KL散度对琴的数据进行两两对比，即：

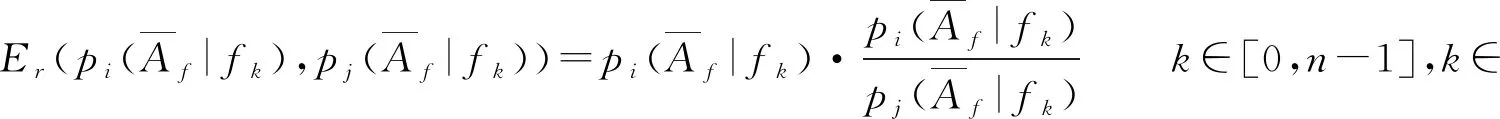
(9)

式中：i和j代表任意两把琴；k代表各频率比值点.

此时得到的结果是6把琴在各频率比值点(k值)处的两两比较的数据.下一步，我们使用假设验证来调查其中各频段上是否有显著差异.作如下假设：

H0:μ≤μ0,H1:μ>μ0.

(10)

假设H0(原假设)认为在此条件下，该处谐音无显著差异；假设H1(备选假设)认为在此条件下，该处谐音具有显著性差异.6把琴两两对比，我们得到15组数据，且总体标准差未知，所以选择t检验，即：

(11)

表2 假设验证的情况

经过以上9组假设验证，我们将具有明显差异和不具有明显差异的谐音进行统计，结果如表3所示.

表3 假设验证结果统计

4 讨论及未来工作

通过使用高斯混合模型为小提琴谐音能量建模，KL散度分析两两数据间的差距，以及假设验证不同谐音的差异性是否显著，最终我们得到了关于谐音能量在分布规律上的不同(表3).

表3中我们可以看到，当拟设均值增大以及显著性水平减小时，具有明显差异的谐音数量减少.在调查的小提琴前12号谐音中，依据谐音能量分布规律的差异显著性，我们将其分为3个等级： 首先，5号、9号、11号谐音具有的差异显著性最低，因为这3个谐音在预设值变化时，最先呈现出差异无显著性；其次，6号谐音始终表现出十分显著的差异，2号和12号谐音只有在假设验证第⑨组情况中才表现出显著性降低，因此，本文认为2号、6号和12号谐音的差异显著性比较高；最后，其余3号、4号、7号、8号和10号谐音，差异的显著性处于中等水平.

结果数据中，第5号谐音每把琴模型之间差异的显著性很低，其原因可能是小提琴这件乐器本身造成的，即有可能第5号谐音的能量分布规律是小提琴的共性.而结果显示第6号谐音各模型间差异非常显著，本文认为这个谐音是小提琴谐音中差别最大的一个.关于第5号谐音能量分布差异性小、第6号谐音能量分布差异性大，以及其他谐音呈现出不同的差异显著性，是作者下一步需要深入研究探讨的.

5 结 语

本文提出了一种研究小提琴谐音分布的模型分析方法.将大量的小提琴演奏的单音作为分析样本，提取频谱信息，从频域的角度为小提琴的谐音能量分布建立模型.从对比研究不同小提琴模型间的差异，来调查小提琴谐音分布规律的差异性，以及差异的显著性.实验结果证明，此种方法对于调查谐音间的差异是有效的.

实验结果说明： 在本文提出的研究方法下，小提琴谐音呈现出有区别的差异性分布规律，不同谐音差异显著性不同.若研究乐器和乐器之间、音色和音色之间的共性特征，应当选择差异显著性较小的谐音重点分析研究；若进行乐器差别、音色差别的研究，应当着重考虑差异显著性较大的谐音.本方法比传统方法研究单一样本的实验结果更具有概括性.此外，本方法还可以用在诸多方面，如研究和评价乐器质量、调查高质量乐器与低质量乐器之间的谐音差异；与乐器制作工艺相结合，利用谐音研究指导和促进乐器制作；以及识别乐器、声音等方面.