Automatic Marking of Single-tone and Chord Piano Fingering Based on Hidden Markov Model
, , ,
(1. School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China;2. School of Microelectronics, Tianjin University, Tianjin 300072, China)
Abstract: A method based on Hidden Markov Model(HMM) for automatic annotation of piano fingering for both hands is proposed. In HMM, the form of fingering is the hidden state and the output note is the observed state. The method mainly has two steps: determining all the transition and emission probability of the HMM and using Viterbi algorithm to search for the most likely sequence of the state of fingering given the sequence of notes. HMM in the method can process both the single note and the chord simultaneously. And the feasibility of the method was verified by the real piano pieces.
Keywords: piano fingering; hidden Markov model; Viterbi algorithm
Fingering is one of the most essential techniques for piano performance which may affect musical expression. Appropriate fingering may facilitate fluency of playing, especially for Allegro. Though there exists an optimal fingering sequence for every piano score in theory, searching for such an ideal fingering still depends on experience and trial-and-error mostly in practice. Besides early rule-based method, machine learning provides a new paradigm for the fingering sequence generation problem. The automatic fingering annotation for any piano score can save the time for exploration, eliminate the early playing obstacle for amateurs, and provide an initial reference fingering scheme for pianists.
To the best of our knowledge, automatic piano fingering annotation can be divided into two categories, rule-based method with the idea of dynamic programming and statistical one such as Hidden Markov Model(HMM).
Dynamic programming is commonly applied to generate the piano fingering[1-3]. In the former study, the researcher divided the task of deciding the fingering into the short sequence and the long sequence parts[1]. For the short sequence, all the possible fingering were listed and ranked by evaluating the difficulties of them according to the specific rules. For the long sequence, the author used the traditional dynamic programming method to find the shortest path with the least cost, which was also defined according to some rules. The cost of the fingering was defined and the cost of performance was aimed to minimize[2-3]. The cost corresponds to the stretch induced by hand position and the transition between two notes. And then they use a trellis graph to represent the piece of music and try to find path with the minimum cost.
The dynamic programming is also used in many more rules which are introduced to evaluate the sequence of fingering[4].
Some researchers create a graph-based fingering generation algorithm named SFG which generates piano fingering for MIDI events in real-time[5]. The algorithm is divided into two layers. The upper layer called Note Processor checks the incoming MIDI event and controls the progress of fingering generation. The lower layer called fingering generation layer is based on the idea of dynamic programming.
For the statistical method, researchers used HMM as a ‘mealy machine’[6], by which the output probability of one fingering state depended on both the previous output and the current fingering state. The fingering state includes the finger form and the finger position on the key. The author manually set the parameters of the transition probability in HMM and uses the Viterbi algorithm to figure out the sequence of fingering states with high probability. However, this method only focused on the single note instead of the chords.
The method proposed later[7]as well used the idea above but the author introduced a modified HMM named merged-out HMM. The author thought that the one-order HMM could not incorporate all the probabilistic constraints between two successive notes while the higher-order HMM would result in too many parameters. Thus two parallel HMMs were used and the outputs of both were merged.
In this paper, we proposed a model based on hidden Markov model, which is suited for modeling the music consisting of chords and is applied for both hands.
1 Automatic piano fingering annotation model
1.1 Model of fingering with HMM
The hidden Markov model consists of the hidden (unobserved) sequence and the observed one. And the hidden sequence can be predicted through transition and emission probability in HMM. As to fingering annotation, the piano score can be considered as a sequence of notes, which is deemed as the observed sequence in HMM, and the fingering sequence corresponding to the note is the hidden one. Let’s set the hidden state asSt, the observed state asOt. An assumption of Markov model is made here that the distribution of any state only depends on its previous state. That assumption can be expressed as
P(St|S1,S2,S3,…,St-1)=P(St|St-1),
(1)
we also assume that the output of one fingering state only depends on that fingering state itself, therefore the emission probability can be expressed asP(Ot|St), which is a conditional probability. Thus the transition probability can be represented asP(St|St-1). Based on such an assumption, we can calculate the transition and emission probability of all the states by
(2)
(3)
In respect ofP(Ot|St) andP(St|St-1), we know that
P(Ot|St)=P(Ot,St)/P(St),
(4)
P(St|St-1)=P(St,St-1)/P(St-1).
(5)
1.2 Estimation of the parameter of HMM
As forP(Ot,St) in equation (2), with enough annotated piano score, we can obtain #(St) which denotes the number of the times of appearance of a certain stateSt, and #(Ot,St) which denotes the number of the times of appearance of bothOtandStsimultaneously. ThenP(Ot|St) can be easily calculated by using #(St) to divide #(Ot,St). This is only an estimation of the probability but as long as the data is sufficient enough, the estimation is reasonable. In addition,P(St|St-1) in equation (5) can be acquired by using the same method:P(St|St-1)=#(St-1,St)/#(St-1). In our paper, we collected 10 000+ notes of each hand which can help us estimate the probability. However, the amount of data is still relatively small, thus we need to enlarge the dataset in the future work.
In our method, we mainly aim to set and ensure the value of parameters of HMM in the learning process. Since HMM consists of the transition probability and emission probability, we will focus on these two parts separately.
In section 1.1, we know that the sequence of fingering states is considered as the hidden sequence and the sequence of notes is deemed as the observed sequence. The states of fingering can be categorized as single finger state, two fingers state, three fingers state, four fingers state, and five fingers state. The number of the multi-finger state are all combination of the five fingers. Except the single-finger state, all the other states correspond to the chords. Thus the total number of the fingering states is 31.
Similarly, the states of notes can be categorized as the single-note and the chord one. Considering 88 keys in a piano, we aim to find out all the possible combinations of the notes. Given the physical limitation in the piano performance, we restrict the maximum range between two notes in an octave. Unlike the measure mentioned above[6], in which the author only considers the notes in one octave, we analyze the total 88 keys. Since in the real performance, the notes for the left hand consist of more chords than those in the notes for the right hand, we will mainly discuss the situation for the left hand first. In the piano keyboard, we start from the first octave and consider all the octaves before the last octave on the right side of the keyboard. In each octave, there are 5 ebony keys and 8 ivory keys. Therefore there are totally 13 keys in an octave. The different situations for different number of fingers are:
Thus the total number of states is 61929.
Under such circumstance, we constructed 2 matrices for both transition probability and emission probability. The size of the transition probability matrix is 31×31 and the size of the emission probability matrix is 31×61929.
1.3 Automatic fingering annotation
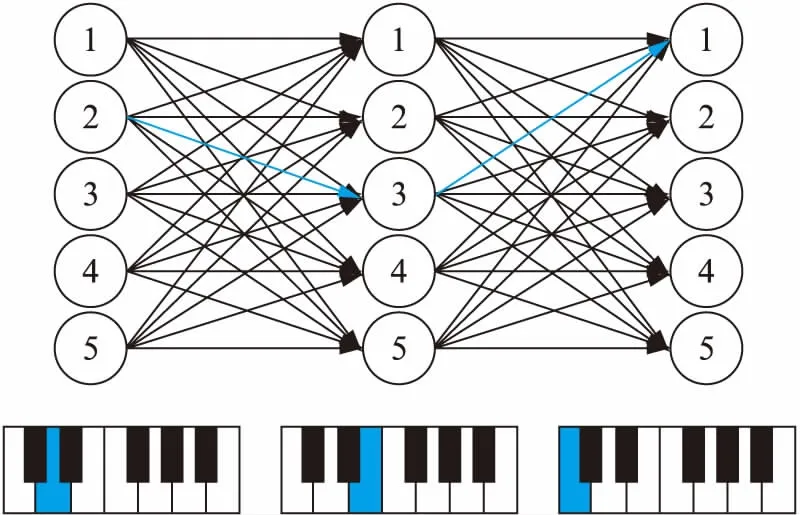
Fig.1 Fingering estimation by Viterbi algorithm
After obtaining the transition probability and emission probability, it’s common and useful to introduce the Viterbi algorithm to predict the hidden state by using the observed state. For each observed state, the Viterbi algorithm aims to calculate the probability of all the potential combination of the hidden state and the observed state. As shown in Fig.1, there’re three states (observed states) in the sequence of notes (D4, C4, E4), and there are 5 fingering states(hidden states) which correspond to the note with different emission probability and transit to the next state with different transition probability.
This algorithm generates a pathS=(s1,s2,…,sT), which is a sequence of statessn∈X={x1,x2,…,xk} that generates the observationsO=(o1,o2,…,oT). The pathSis supposed to have the largest probability or to be the shortest path.The algorithm is based on the principle that for a stateST, the temporary pathSshould be the shortest path or the path with the largest probability. When we would like to move on to the next stateST+1, we only need to consider the distance betweenST+1andST. It’s necessary to construct twoK×Kmatrices at each step since we need to calculateK×Ktimes between two fingering state.Thus we only need to do the calculation between two neighboring states in the calculation and the complexity is limited withino(K2)=o(N2). In our study,Srepresents the fingering state andOstands for the note. Our aim is to find the path with the largest probability. The transition probability between the states is deemed as the distance of the path. Let’s take the graph in Fig.2 as an example.
O1,O2,O3correspond to D4, C4, E4 on the keyboard. Thus the target is to find a path which goes through the graph with the largest probability. Firstly we find out the 5(K=5) value of the initial probability of the first stateP(O1|S1) and multiply them withP(S2|S1)·P(O2|S2), filling the 25 values into the matrix ofO1andO2. And then we obtain a largest probability corresponding to a specific path for each fingering of the stateO2. Then we multiply the probability we obtain forO2withP(S3|S2)·P(O3|S2), filling the 25 values into the matrixofO2andO3. And then we again obtain a largest probability corresponding to a specific path for each fingering of the stateO3. The largest probability among the 5 probabilities ofO3corresponds to the path we seek for. In our example, the path which goes through (2,3,1) has the largest probability. Therefore we think that using the index finger, the middle finger and then the thumb to play the note (D4, C4, E4) is the best choice.
2 Experiment and discussion
2.1 Preparation for the dataset
Since we use the supervised method to decide the model parameters, we need to collect enough data. In our experiment, we mainly focus on the piano textbook since the fingering in such pieces in the textbook are relatively typical. We chooseBach28ShortPiecesforPiano(28 pieces),Cherny299(10 pieces), andABRSM(Associated Board of the Royal Schools of Music)ExamPieces2017(35 pieces from level 4 to level 7),and collect more than 70 pieces of scores which includes more than 10 000 notes for each hand.
2.2 Character of the dataset
It’s obvious that in Section 1.2, we construct a matrix containing 31×61929 parameters and it seems unrealistic to manually label too many pieces. Thus it’s of great importance to set some constraints of the matrix to reduce the demanding number of parameters. Let’s take the left hand as an example. In a real piano performance, it’s impossible for the performer to click on all the single key of the equal possibility, which means that the chance of clicking on each key is subject to a probability distribution. The distribution of the single note and chords is shown in Fig.2(see page 354).
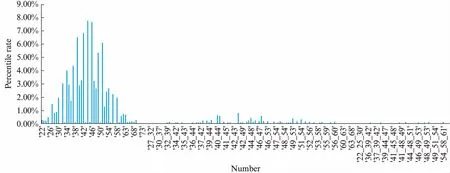
Fig.2 Distribution of the single note and chords
The result shows that the notes which appear in a piece of music are commonly limited to a small range. What’s more, since the single-finger state can only output the single-note state, the full 31×61929 matrix can be divided into 5 sub matrices (5×88, 10×978, 10×5236, 5×17215, 1×38412). In addition, it’s commonly acknowledged that the 5-finger state is rare in the real performance and we haven’t acquired the data containing the 5-finger chord, so we choose to simplify our parameter matrix by ignoring the 5-finger state.
We acquire #(Ot) and #(St) which stands for the number of the times of appearance of a certain outputOtand stateSt, then calculate the transition probability and the emission probability. The result is shown in Tab.1 and Tab.2.
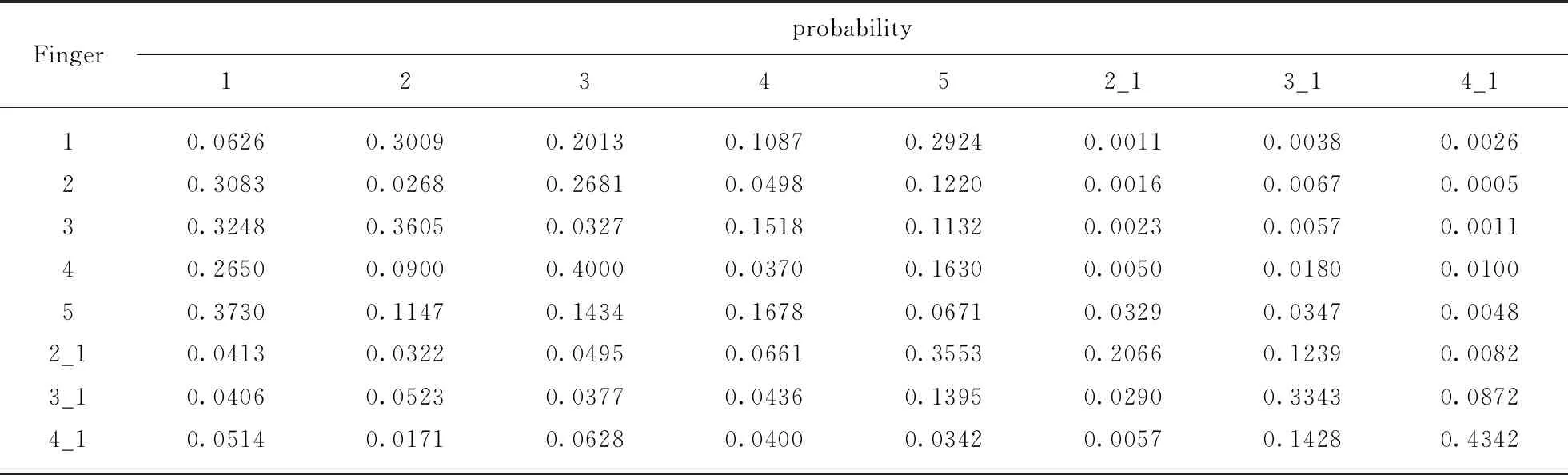
Tab.2 Part of the emission probability
2.3 Result and discussion
In order to validate the reliability of the model, it’s necessary to use cross validation. In our experiment, we choose the 5-fold cross validation, in which the dataset is divided into 5 groups. Here we introduce a fault-tolerant mechanism. As we all known that the thumb, index finger and middle finger of our hands are more flexible than the ring finger and little finger, it’s reasonable for us to tolerate the error if we replace one certain finger with its neighbor finger. For example, if the chord is performed by the little finger and the middle finger (′3_1′) and our model outputs the little finger and the index finger (′2_1′), we still deem the result as correct output. This kind of situation is shown as Fig.3.

Fig.3 The fingering of two-finger chord
These situations of 2-finger chords can also be extended to 3-finger chords, which means that (′5_3_1′) and (′5_2_1′) are both accepted. In addition since the chords appear much more times for left hand, we do our experiment for the left hand. After such kind of fault-tolerant processing, our average accuracy of 5-fold validation is 55.67%.

Tab.3 Accuracy of the fingering annotation
In the former method of Merged-output HMM[7], the author tested their model on the Bach’s Two Invention including Nos.1, 2, 3 and 8. We do the same test on those pieces and the result is shown in Tab.3. By introducing the fault-tolerant mechanism, our model can perform better than the Merged-output HMM[7], and that mechanism is really reasonable since the piano performer sometimes may not be able to tell the difference between using the index finger and the middle finger.
3 Conclusion
3.1 Advantage
The advantage of our proposed method includes the following.
(1) The chord in the piece of music is handled as one single state, instead of several continuous states. Because if we divide a chord into several single note and put them in a sequence, the emission probability of a multi-finger state may be interfered by the other single-finger state. But this phenomenon will not appear in our method.
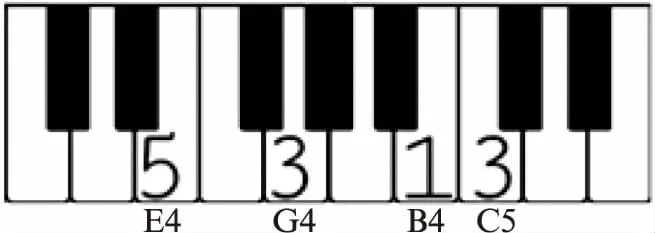
Fig.4 The fingering of two neighboring states
For example, as shown in Fig.4, if there are two neighboring states, a chord of E4_G4_B4, and a single note C5, we probability prefer using the little finger, the middle finger and the thumb to play the chord and using the middle finger to click on C5 which needs the finger-crossing. However, once we break the chord into 3 single note, it cannot be neglected that the difficulty of playing C5 after a single note (the chord is transformed to the arpeggio) does not equal to the difficulty of playing C5 after a chord. It may take a bit of time to move your whole hand from the left side to the right side which may result in the low transition probability. As a result, our method considers such kind of detail which are neglected in other method by processing the chord as whole.
(2) In the process of deciding the fingering, there are some physical limitations that we need to consider:
a) The thumb, the index finger and the middle finger are more flexible than the ring finger and the little finger, thus we shouldn’t use the ring finger and the little finger frequently to perform some difficult action such as finger crossing.
b) The finger crossing likely occurs in the transition between the thumb and one of the other fingers. And performing the finger crossing frequently is of much difficulty.
c) It’s difficult to play an ebony key by the thumb and to play an ebony key by the finger after finger crossing.
Given those physical limitation, we have already overcome those difficulties by incorporating the habits of performance in our data.
(3) Unlike the former study based on HMM[6-7], the left hand and right hand are processed separately. In the former study, there exist a difficulty doing the separation between the left hand and the right hand which may cause the error. However, in our experiment, we take the MusicXML file as the input instead of the MIDI file. While it’s complicated to process the MIDI file and the left hand notes and right hand notes are not separate, MusicXML is a great file type which can help us process the left hand and right hand separately.
3.2 Improvement
The statistical method we use has the weakness that the model outputs is easily influenced by the specific data when the dataset is not large enough. For example, since our dataset contains around 70 pieces of music, once the tendency of the fingering in several pieces of music are extremely different from the tendency in other pieces as the specific finger position and form appear repeatedly for many times, then the fairness of the distribution of the transition probability and the emission probability of our model may decrease and the error of our model may increase. For example, in our experiment, there are too much finger-crossing phenomena in the train set in a specific octave. As a result, when we use that model to test on other validation set which does not include finger-crossing, the accuracy will be greatly impacted. There are two potential solutions:
1) Manually control the dataset before training;
2) Manually adjust the transition probability and emission probability matrix.
Simultaneously, it’s necessary to keep on enlarging the dataset in order to make our model apply to more pieces of music including various kinds of notes.
4 Future work
The statistical model with supervised method requires a large amount of data. However, it’s not realistic for us to manually label enough notes to enlarge the dataset. Therefore we may do some study on the unsupervised method in the future and combine the supervised method with the unsupervised one to improve the performance of our model. Baum-Welch algorithm is commonly used in the unsupervised method thus we probably implement that algorithm in our work.
5 Summary
This paper proposed a method for automatic annotation of piano fingering based on HMM. We model the piano performance by a sequence of hidden states corresponding to a sequence of output states. The hidden state represents the finger state and the output state represents the note. After obtaining the transition probability and the emission probability, the most probable fingering is acquired by using the Viterbi algorithm. This method shows the great value in guiding people to play the piano appropriately. As the method is gradually improved in the future work, it will show much more value in practicability.
Acknowledgements
The authors would like to express thanks to Zhang Yunrui, Gao Ya and Li Xingchen for their assistance in manually annotating the fingering.

