两种群间的疾病交叉传染模型*

郑 伟

(楚雄师范学院数学与统计学院，云南 楚雄 675000)

1.引言

传染病〔Infectious Diseases〕，是由各种病原体引起的能在人与人，动物与动物或人与动物之间相互传播的一类疾病[1]。在历史上，传染病所造成的危害巨大。一直以来，很多科学家都在从事传染病的研究，特别是在20世纪期间，取得了辉煌的成果。但随着国际贸易与交往的发展，生态环境的变化以及病原体和传播媒介抗药性增强，原来灭绝或者得到控制的传染病再次开始抬头，来势汹汹，形势严峻。历史和现实都告诉我们，人类面临着种种传染病长期严峻的威胁，对传染病的防治任重而道远，它仍然是人类的“第一杀手”[2―5]。

由于对传染病的研究不能采取试验形式，因此，对各类传染病发病机理，流行规律，预测预报就更多发地需要理论分析，定量分析，模拟仿真来进行，而上述分析都离不开针对各类传染病而建立的数学模型[6]。建立数学模型对传染病传播规律进行理论研究是理论传染病学的一种重要方法.利用传染病模型可以对影响疾病传播的生物学和社会机理进行清晰的描述，通过对模型的研究来揭示疾病流行规律，预测流行趋势，为发现、预防和控制疾病的流行提供理论依据和策略。数学模型也是检验理论和定量评估猜想与结论的实验工具[2]。

在传染病模型中，最常见的经典模型有SI模型，SIS模型，SIR模型以及SEIR模型等.其他常见的模型还有SEI模型，SEIS模型，SIRS模型，SEIRS模型等。

2. 基本定义及符号说明

定义2.1[7]每个病人单位时间有效接触的人数称为日接触率，记为λ.

定义2.2[7]病人每天被治愈的人数占病人总数的比率称为日治愈率，记为μ.

定义2.3[8]在一个传染期内病人有效接触的平均人数称为传染病期内的接触数，记为σ=λ/μ.

定义2.4[9]易感染者(Susceptible)，其数量记为S(t)，表示t时刻未感染但有可能被该类疾病传染者的数量。

定义2.5[9]染病者(Infective)，其数量记为I(t)，表示t时刻已被感染成为病人并且具有传染该种疾病的人数。

定义2.6[2]移除者(Removed)， 其数量记为R(t)，表示t时刻已从染病者中移出的人数。

定义2.7[2]潜伏者(Exposed)， 其数量记为E(t)，表示t时刻已被感染但还没有发病的人数。

定义2.8[2]每一个易感染者染上病毒后，并不马上变成病人，而有一段滞后的时间才变成传染者，这段滞后时间称为潜伏期，记为τ。

本文还用到如下记号：

N1—种群甲的总数量(以下简称甲)；

N2—种群乙的总数量(以下简称乙)；

s1(t),i1(t),r1(t)—分别表示甲中易感染者，已感染者和移除者占甲的总数的比例；

s2(t),i2(t),r2(t)— 分别表示乙中易感染者，已感染者和移除者占乙的总数的比例；

λ11,λ12—分别表示甲相对甲(以下记为甲-甲)与甲相对乙(以下记为甲-乙)的日接触率；

λ21,λ22—分别表示乙相对甲(以下记为乙-甲)与乙相对乙(以下记为乙-乙)的日接触率；

μ1,μ2—分别表示甲，乙的日治愈率；

σ11=λ11/μ1,σ12=λ12/μ1— 分别表示甲-甲与甲-乙的接触数；

σ21=λ21/μ2,σ22=λ22/μ2— 分别表示乙-甲与乙-乙的接触数。

3.主要模型

基于传统的单种群模型的建模思想和基本手段，本节主要研究在只考虑影响两种群间传染病传播的最基本因素之一，即日接触率的情况下，两种群相互作用的疾病交叉传染模型，不考虑两种群间的捕食、竞争关系、各种群的出生率、死亡率和迁移活动，从而得到疾病在两种群间的交叉传染模型。自Kermack和Mckendrick于1927年构造了经典的SIR仓室模型以来[9]，传染病模型一直被广泛研究。对于一般的传染病模型，它只考虑了单个种群，得到了一些“阀值理论”。然而实际情况并非如此。在生态圈中，各个种群并非孤立存在着。因此，对疾病在相互作用种群之间传播规律的研究更具生物意义。由于问题涉及的是两个种群相互作用的传染病模型，与单种群传染病模型相比较而言，由于两种群间影响传染病传播的因素大大增加，因而也会导致模型的维数升高，从而也更加增大了分析的难度，如何将其有效地降维也就成了两种群相互作用下传染病模型的一项首要任务。对此，本文并未进行深入研究探讨以求出精确解，仅作初步建模及简单分析。

3.1两种群相互作用下的SI模型

(1)模型假设：

假设1：在疾病传播期内所考察的甲，乙两个种群的总数量N1、N2不变.不考虑甲、乙的出生、死亡、迁移以及相互间的竞争和捕食关系，将甲、乙分别分为易感染者和已感染者两类，记t时刻这两类群体分别占各自种群总数的比例为s1(t),i1(t)和s2(t),i2(t)，则有

s1(t)+i1(t)=1,

(3-1)

s2(t)+i2(t)=1.

(3-2)

假设2：甲-甲与甲-乙的日接触率分别为λ11,λ12；乙-甲与乙-乙的日接触率分别为λ21,λ22.

(2)模型建立

根据假设，可以得到甲，乙的成员流动框图如下:

图3―1 两种群间的SI模型框图

图3―1中，λ11s1(t)N1i1(t)是因甲的病人与甲的健康者有效接触从而使甲的病人数N1i1(t)增加的增加率，即甲的健康人数N1s1(t)被甲的病人感染而减少的减少率，λ21s1(t)N2i2(t)是因乙的病人与甲的健康者有效接触从而使甲的病人数N1i1(t)增加的增加率，即甲的健康人数N1s1(t)被乙的病人感染而减少的减少率;同理，λ22s2(t)N2i2(t)是因乙的病人与乙的健康者有效接触从而使乙的病人数N2i2(t)增加的增加率，即乙的健康人数N2s2(t)被乙的病人感染而减少的减少率，λ12s2(t)N1i1(t)是因甲的病人与乙的健康者有效接触从而使乙的病人数N2i2(t)增加的增加率，即乙的健康人数N2s2(t)被甲的病人感染而减少的减少率.再记初始时刻甲，乙中易感染者数和已感染者数分别为s1(0)、i1(0)、s2(0)、i2(0)且s1(0)=s10、i1(0)=i10、s2(0)=S20、i2(0)=i20.因此，可根据图3―1得到两种群相互作用下的SI传染病模型为

(3―3)

(3)模型讨论

对λ21,λ12的取值进行讨论:

(i)当λ21=0,λ12≠0时，传染病在甲种群内的传播不受乙影响，但在乙种群的传播受甲的影响.此时，对甲有

(3―4)

由模型(3―4)得

(3―5)

方程(3―5)是Logistic增长模型[8]，它的解为

(3―6)

式(3―6)就是该传染病在甲种群中单独传播的传播规律(即为传统的单种群下的SI模型).

在该传染病的传播规律中，根据(3―6)式，显然，病人数量i(t)单调递增，且当t→∞时，有i→1，这表明如果任其发展而不采取积极有效的措施，最终所有人终将被传染变为病人，这显然也是不符合实际的.尽管如此，在传染病流行的前期这个模型还是可用的，因而传染病的学者曾用它来预报传染病高潮的到来时刻[8].

模型失败的原因是在模型中，没有考虑到病人可以治愈，人群中的健康者只能变成病人，而病人不会变成健康者，这与实际情况是相悖的.

另外，对乙种群有

(3―7)

从模型(3―7)可以看出，采取隔离措施是有效控制该疾病在种群乙中传播的途径之一.当λ12=0,λ21≠0时，情况类似.

(ii)λ21=λ12=0时，说明甲乙之间不会互相传染此种疾病，隔离措施失效.

(iii)λ21≠0且λ12≠0时，应及时采取隔离措施将两种群隔离，避免两种群间的互相接触.

此外，无论λ21,λ12如何取值，提高治疗水平和改善种群的生存环境是控制疾病在种群(无论是多种群还是单种群)间传播的有效并且是切实可行的重要途径.

3.2 两种群间的SIS模型

对于有些人畜共患或多种群共患的传染病等治愈后免疫力很低，可以假定无免疫性，于是各种群中患病者被治愈后变成健康者，健康者还可以被感染成为患病者，其成员流动形式为:S→I→S，故将该模型称为SIR模型.

(1)模型假设：

模型假设1和2与SI模型的假设1，2相同，另新增如下假设条件:

假设3：μ1,μ2分别是甲，乙的日治愈率，1/μ1, 1/μ2分别是甲，乙的平均传染期.

(2)模型建立

以下是两种群间SIS传染病模型框图:

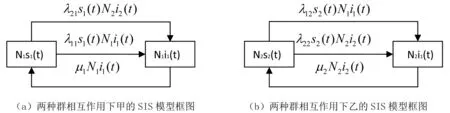
图3―2 两种群间疾病交叉传染的SIS模型框图

由图3―2可知，λ11s1(t)N1i1(t)+λ21s1(t)N2i2(t)是甲中已感染者N1i1(t)的增加率，μ1N1i1(t)是甲中已感染者被治愈后仍可被感染的增加率；同理，λ22s2(t)N2i2(t)+λ12s2(t)N1i1(t)是乙中已感染者N2i2(t)的增加率，μ2N2i2(t)是乙中已感染者被治愈后仍可被感染的增加率.

由此，可得到两种群间疾病交叉传染的SIR模型为

(3―8)

其中，s1(0)=s10,i1(0)=i10和s2(0)=s20,i2(0)=i20分别为初始时刻甲，乙中易感染者和已感染者在各自种群中所占总数量的比率。

(3)模型讨论

(i)当λ21=0，λ12≠0(或λ21=0，λ21≠0)时，可视该类疾病是在飞禽与走兽之间传播的传染病，其中值为零的表示走兽相对飞禽的接触率，说明飞禽与走兽之间并没有直接的接触关系，走兽被感染该类疾病可能是由于食用了飞禽的残骸或粪便等其他原因。

(ii)控制该类疾病在两种群间的传播的手段有:(1)种群隔离(若λ21=λ12=0，该措施失效)；(2)隔离治疗；(3)阻断疾病的传播源等。

(iii)在某些情况下，引入新的种群也可以避免该类传染病的流行。

3.3两种群间疾病交叉传染的SIR模型

对于传统的单种群模型而言，SIR模型是最经典的模型之一.它的建立为发现，预测和控制诸如天花，麻疹，甲肝等治愈后有很强的免疫力的传染病的流行规律和病理机制提供了理论依据和方案策略.在人畜共患或禽畜共患等多种群相互作用的传染病当中，也存在着这类治愈后具有很强的免疫力的疾病，因此，建立两个或两个以上的种群相互作用下的SIR模型对这类疾病进行研究分析并将其理论结果运用于实际案例当中也一样的重要。

(1)模型假设：

(i)甲，乙的总数不变，其数量分别为N1,N2。将甲，乙分别分为易感染者，已感染者和病愈免疫的移出者三类，记t时刻这三类群体分别占各自种群总数的比例为s1(t),i1(t),r1(t)和s2(t),i2(t),r2(t)，则有

s1(t)+i1(t)+r1(t)=1,

(3―9)

s2(t)+i2(t)+r2(t)=1,

(3―10)

(ii)甲-甲与甲-乙的日接触率分别为λ11,λ12;乙-甲与乙-乙的日接触率分别为λ21,λ22.

(iii)μ1,μ2分别是甲，乙的日治愈率，1/μ1, 1/μ2分别是甲，乙的平均传染期;记甲-甲与甲-乙的接触数分别为σ11=λ11/μ1,σ12=λ11/μ2，乙-甲与乙-乙的接触数分别为σ21=λ21/μ1,σ22=λ22/μ2.

(2)模型建立

按照SI和SIS的方法，先作出SIR模型的成员流动框图:

图3―3 两种群间疾病交叉传染的SIR模型框图

在图3―3中，λ11s1(t)N1i1(t)+λ21s1(t)N2i2(t)是甲中已感染者N1i1(t)的增加率，μ1N1i1(t)是甲中已感染者每天病愈免疫移出者的增加率;λ22s2(t)N2i2(t)+λ12s2(t)N1i1(t)是乙中已感染者N2i2(t)的增加率，μ1N2i2(t)是乙中已感染者每天病愈免疫移出者的增加率。由此得到模型:

(3―11)

以上就是疾病在两种群间交叉传染的SIR模型.其中，s1(0)=s10,i1(0)=i10,r1(0)=r10=0和s2(0)=s20,i2(0)=i20,r2(0)=r20=0分别为初始时刻甲，乙中易感染者，已感染者以及病愈免疫移出者在各自种群中所占总数量的比率。

(3)模型讨论

以下是控制该类疾病在两种群间的流行和蔓延的有效手段:

(i)可以通过种群隔离或隔离治疗降低甲-甲，甲-乙，乙-甲和乙-乙的日接触率λjk(j=1、2，k=1、2)；

(ii)提高医疗卫生水平，其一是可以提高日治愈率，降低患者数，也降低了每天被感染的健康者人数，其二是可以减少病原体的传播途径；

(iii)进行预防接种使群体免疫，这个手段可以使健康者接种后成为具有免疫力的群体直接移出模型系统。其成员流程图如下:

图3―4 采取预防接种后甲，乙各成员的流动图

4.总结

传染病在现实生活中无处不在，常常给人类和社会带来严重的危害，例如刚刚过去的甲型H1N1，禽流感，SIRS以及到目前还未能彻底治愈的AIDS等都给人类带来了极大的威胁。因此，研究传染病传播的数量规律，建立有效的防控机制既是摆在我们面前的一个困难课题，也是一项紧迫任务。传统中对传染病模型的研究，往往只考虑了单个种群，得到了一些阀值理论，然而实际情况并非如此。很多传染病不仅仅只在单一种群中传播，也会在多个生物群体间相互传染，并且造成的后果相当严重。在生态圈中，各个种群也并非孤立存在着。因此，本文研究疾病在两种群之间传播规律比传统只对单一种群的研究更具生物意义。