数学意境的文学表达*

郭培俊

（浙江工贸职业技术学院,浙江温州325003）

一、数学意境的含义

数学与文学，感觉疏远，其实两者之间也有一座无形的“鹊桥”贯通，这便是——意境。

意境是指作品中所描述的形象和表现的思想感情融合一致而形成的一种艺术境界[1]。意是情与理的统一，境是形与神的统一，情理、形神相互渗透、相互制约就形成了意境。文学有意境，小品有意境，戏剧、电影电视都有意境。如果把数学公式、数学图形、数学符号理解为数学的形，那么，数学概念、数学定理、数学法则则可以理解为数学的神。数学意境，就是数学形与神所表达的数学思想。

意境，是文学和数学所能通达的共同境界，共同的理想势态：

（一）文学意境和数学意境都具有三个特点。文学意境：表真挚之情、状飞动之趣、传万物之灵趣，数学意境：表永恒真理、状变化规律、传“万物皆数”之灵。

（二）文学意境和数学意境的结构特征均是虚实相生。意境由两部分组成：一是“如在眼前”较实的因素，称为“实境”；二是“见于言外”较虚的部分，称为“虚境”。虚境是实境的升华，体现着实境创造的意向和目的，体现着整个意境的艺术品位和审美效果，制约着实境的创造和描写，处于意境结构中的灵魂、统帅地位。虚灵性是意境的又一特征[1]。数学知识也往往具有高度抽象性，一个虚数单位就是集抽象性和灵性于一身的典型代表。

（三）文学意境具有“得意忘象”的情理，而数学也具有“得意忘形”情理。比如导数的几何意义是曲线上切点处切线的斜率，但它抽象意义或实质却是函数增量与自变量增量比值的极限，一旦理解了导数的实质，在进行导数计算时，就可以暂时忘掉其几何意义——切线的形。

《高等数学》一些概念和定理，抽象性强，定义严谨，尤以初学者难理解，更难以达到熟练掌握程度。通过学生熟知的文学作品，比如唐诗宋词、成语警句等的引入，借用文学意境的表达，来帮助学生领悟数学概念、公式的意思或含义，撇开数学讲数学，看似走了弯路，实则是曲径通幽，收到“山穷水复疑无路，柳暗花明又一村”的奇效，能快速达成教学目标。

毕竟，数学具有高度抽象性。一个极限的概念就让人费解（可以表达但难以意会），一个无穷小的概念，由模糊至清晰也难以琢磨透彻，导致数学史上产生第二次危机，差点让《微积分》坍塌，等等。数学的发展不是一帆风顺的，其传授也是困难曲折的。数学教育史上，有人回避无穷小，想重构高等数学，但以失败告终；有人回避极限的精确定义，采用定性方法重新定义了极限，如今的高职高专教材便是出此一辙，但很难达到数学的精确境界。如何简要而又完整传达数学的精髓，把数学的意境表现出来，是《高等数学》教学的最高境界。

当用数学语言直接表达数学概念难以理解时，特别针对初学者，可借用学生熟悉的文学意境迁移过来，籍以类比转化成数学概念的意境，达到“醉翁之意不在酒，在于山水之间也”的效果。

二、数学意境与文学对应的三种方式

（一）数学的神借助文学的景来表达

数学是关于符号的学问，数学定义、定理，往往要用符号来表达，言简意赅，但对初学者而言，往往显得过于抽象、难懂。数学含义、数学思想（神）借助于文学情景的再现来类比联想，达到化抽象为具体、复杂为简单的神奇效果。

1.“邻域”概念教学。研究函数在某点左右附近的局部性质需介入“邻域”概念。有学生发现“邻域”就是中学所学开区间，两者有什么区别？《高等数学》为什么开篇就讲“邻域”概念？此时引出“近朱者赤，近墨者黑”（晋·傅玄《太子少傅箴》）成语典故，取其原意，说明要描述一个函数的性质和特征，只须通过观察分析局部某些点的性质和特征就可以推断整体情况了。采用逆向思维，把成语改成“赤者近朱，黑者近墨”其意境更胜一筹，用来比喻高等数学构建以“邻域”为重要核心思想方法是奠定数学分析成功的基石，恰如其分。设想：如果只孤立注视一点，它有什么性质?除能求函数值外（点观），却很难发现其他变化的规律，失败原因在于用静止孤立观点看问题；若扩大到整个定义域内观察，由于范围太大，虽能得出一些宏观长期趋势（宏观）规律（如函数的单调性、周期性、有界性），但范围过于宽泛，一些隐藏的性质（中观）却很难发现（如连续性、可导性），或即使发现了却很难描述清楚。“大至无外，小至无内”，“邻域”向外可扩充到无穷区间，小可退缩至一点。“邻域”概念，很多老师不介绍，或蜻蜓点水一下，是教学环节设计中的一个败笔，是没有认识到“邻域”概念作为一种思想方法、策略在高等数学分析中的重要性所致。

2.“向量”概念教学。自由向量的特点是与起点无关，可平移到任何起点处，是为“糊涂”；向量不仅有大小，而且有方向，是为精确。然而，正是与起点的无关性，才有了任意两个向量可以相加、相减、相叉乘的定义，正是有了这种“不管起点在哪”的糊涂性，才有了自由向量的精确性、自由性、完美性。向量的这种糊涂性与精确性的矛盾统一，正如郑板桥的名言“聪明难，糊涂尤难，由聪明而转入糊涂更难”。学好高等数学，有时要具备这种由精确而转为糊涂的策略思想。除了向量以外，在函数单调性、极值判定时，在给定的区间里任取一个数作代表，也正是这种由精确而转糊涂的体现；还有在利用夹副准则求极限、无穷级数的收敛性判定时，往往要运用不等式的放缩技巧，至于放缩到何程度，也是比较糊涂的，只要有效果就行。

3.“连续函数的介值定理及微分中值定理”教学。如果函数y=f(x)在闭区间[a,b]上连续，且

f(a)f(b)＜0,则在(a,b)内至少有一个点c,使

f(c)=0。即方程 f(x)=0在(a,b)内至少有一个根。但这个根究竟在哪，定理并没有指出，是很模糊。

联想到贾岛《寻隐者不遇》的诗句“松下问童子，言师采药去；云深不知处，只在此山中。”人文意境美丽动人，与数学上的介值定理意境十分相通。数学上的存在性定理还有微分中值定理，定理中的点ξ也没给出具体答案，但ξ肯定是存在的。

4.“极限”概念教学。为了对极限有一个形象直观的印象，先让学生朗读诗句：“故人西辞黄鹤楼，烟花三月下杨州。孤帆远影碧空尽，唯见长江天际流”（唐·李白《黄鹤楼送孟浩然之广陵》）。老师在学生朗读时，画出示意图：楼台、长江、帆船，并用x表示帆船与黄鹤楼的距离，用y表示帆船的视觉高度（远影），诗中之景“天际”可形象地用x→∞表示，则整个诗句的意境可表示成：“当x→∞时，y→0”，记作极限的概念和符号顺其自然得以引出[3]。

5.“无界函数”教学。讲无界函数时，引用配画诗“满园春色关不住，一枝红杏出墙来”（宋·叶绍翁《游园不值》），用墙和红杏类比界限和函数，意境优美而又传情达意，原本枯燥难懂的数学概念，变成了富有情感易接受的唯美诗篇，其教学效果不言而喻[4]。

9.“法向量”教学。垂直于平面的向量叫法向量。引用诗句“安得齐天孙大圣，神针底定太平洋”（阿袁《又见》）的意境能形象、直观呈现数学图形和概念本意。

（二）数学的形借用文学的神来表达

高等数学研究的主要对象是函数，绘制函数图形能形象直观地呈现函数的性质，清晰的图像能高效快速促进对函数性质的学习与掌握。记住了图形就能由外及里推知函数的性质和变化规律。但是，当函数图形比较难理解、难记忆时，可以通过文学意境的“意像”来比划，刻痕。还有一些通过不完全归纳法推得的数学公式，包含符号（正负）规律、系数规律、代数式的规律，不易记忆，这些公式的“形”也可以根据其特点，借助于文学意境来刻画。

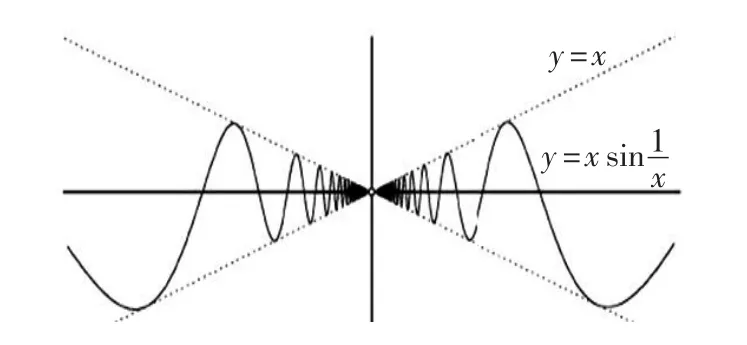
图1 函数y=xsin图像

2.“高阶导数公式”教学。对（高阶导）函数y=anxn+anxn-1+…+a0求一阶、二阶、n阶导数时，最终n+1阶导数净化为0。对求导结果的“形”借成语“一代不如一代”的“神”来传达，强调其降幂的特点。

对y=erx求高阶导数时，对结果y(n)=rnerx的“形”总结成“青出于蓝而胜于蓝”的“神”，说明核心部分（指数函数）不变而系数变复杂了；对高阶导数提炼成“江山代有人才出”或“层出不穷”。

（三）数学的神借助文学的神来表达

无穷数列、级数，由于无限性，往往比较抽象，神奇难料。但其精神（思想）与文学中的诗词、名言、警句的思想是相通的。

图2 《使至塞上》的数学意境

“情与景汇，意与象通”是艺术美的欣赏依据。如前述，可以借助文学来表达数学意境，反过来，也可以借助数学描绘诗词的意境。唐诗绝唱“大漠孤烟直，长河落日圆”（王维《使至塞上》），描绘了一幅空旷荒寂的塞外黄昏景象。如果把“大漠孤烟直”想象成一条垂直于平面的直线，那么就可以把“长河落日圆”想象成一个圆切于一条直线[5]。诗意还可以画成如图2所示。

三、用文学表达数学意境的功效

在数学课上渗透文学，让数学意境通过文学来表达，教师不单单提供纯数学知识，还辅之于文学佐料，作为一种教学“供给侧”改革的探索，其教学功能效果至少有以下4种。

（一）激发学习兴趣，提高学习效率。数学的新概念，抽象难懂，但文学诗句学生是耳熟能详的，而且朗朗上口，让学生在诵读诗文中，体味数学的意境和美感，其乐无穷，兴趣备增。通过文学的意境来旁敲侧击数学的意境，降低了理解难度，学习效率大幅提高。

（二）重启学生自信，拓展学生通识。大多数高职生的中学数学基础差，过去的频繁考试，成绩不理想，对学习数学失去了信心。通过转移话题，借学生熟悉的文学知识来帮助理解数学知识，打通了学习障碍，拓展了思维品质，智商情商皆有提高，素质课堂落地生根，教学效果持续提升。

（三）活跃创新思维，提高创新能力。数学和文学结合，本身就是一种创意，“文学能帮助我们更有效、更深刻地欣赏数学知识与思想”[6]。中小学虽然有那么几个老师进行了点上尝试，但高职院校的《高等数学》课上却鲜见，针对高职生特点（数学基础较薄弱）和课程要求（淡化证明强调应用），更适合采用数学文学相融合的方法，达到定性理解，适度应用的目的。

（四）构建教学方法，改革教学课堂。数学文学的渗透对学生而言，可以激发兴趣、重启对数学的信心，对老师而言，是一种教学创新，一种新型教学风格的塑造；对数学教育而言，是一种教学理念和方式的改革。

意境是数学和文学共同追求的最高境界。数学是一种学问，是一种思想，是一种符号，当然也是一种文化；文学是一种学问，寓一种思想，载一种文字，传承一种民族文化。文学与数学意境都追求：有限与无限的转换；虚与实的跳跃；情与景的融合。

目前经济结构、产业结构都在探索实践供给侧改革，用改革的办法推进结构调整，提高生产率。数学教学借鉴“供给侧”改革理念，通过改变传统的教学方式，降低学生学习的困难程度，助推学生理解能力提高，从而提升课堂教学效率和效果。数学晦涩难懂，用文学语言解释明白，就是一种教学供给侧改革。中国文化博大精深，充分挖掘文学中的思想、方法、意境，对接数学教学，营造轻松和谐的教学氛围，改善课堂教学环境，把数学意境用文学来表达，数学教学的“供给侧”改革将盛开一朵奇葩。