生产调度与预防性维护集成优化*

高 胜，杨宏兵,2，倪 婧

(1.苏州大学 机电工程学院，江苏 苏州 215006；2.广东工业大学 广东省计算机集成制造重点实验室，广州 510006)

0 引言

有限产能批量问题(Capacitated Lot-Sizing Problem，CLSP)是在产能资源受约束的情况下，最小化生产成本，决策产品在连续生产周期内的调度问题[1-3]。然而生产调度的有效实施还取决于设备的稳定性。设备出现故障有两种情况：一是因突发状况导致设备停机的突发故障；二是因设备的退化效应产生不良品的渐变故障。因此制定生产调度方案时需要综合考虑设备的预防性维护(Preventive Maintenance, PM)与故障维护(Corrective Maintenance, CM)策略，以减少不良品生产数量与故障停机次数。

目前，预防性维护与生产调度集成问题已经引起了越来越多的关注。Aghezzaf等[4]提出了生产计划与预防性维护相结合的数学模型，采用周期性的预防性维护策略，但是会发生维护过度的问题。Fitouhi等[5]提出了非周期性的预防性维护与生产调度相结合的模型，并解决了生产计划与维护计划不一致的问题，但存在过度维护的情况。Nijid等[6]讨论了预防性维护与故障维护的关系，并在模型中考虑了缺货成本。蓝天皓等[3]提出了基于设备运行的有限产能批量与预防性维护的生产调度模型，但是维护节点不确定。金垚等[7]利用统计过程控制模型与设备维护进行融合，建立联合经济模型，利用控制图监视生产状态并采取相应的设备维护策略，但没有考虑到生产排产问题。张博文等[8]以CLSP模型为基础，采用基于设备运行的预防性维护与成组维护的策略建立并行机的生产调度模型。崔维伟等[9]针对单机系统提出了联合考虑生产调度与设备维护的联合决策模型。崔维伟等[10]提出了基于多目标优化的生产调度与设备维护模型，利用改进的NSGA-Ⅱ算法求解到Pareto最优解。

上述生产与预防性维护联合建模的相关研究主要侧重于生产调度与设备维护，对质量影响生产调度相关的研究较少，且大部分文献是依据设备故障服从Weibull分布[11]对设备的故障次数进行预测，不能确定设备故障的节点。因此，本文对考虑产品质量的预防性维护与生产调度集成优化问题进行研究，建立联合优化模型并设计相应差分进化算法对其进行求解。由每天的订单需求确定当天生产产品的批量、加工顺序及确定预防性维护的时间节点，使得在满足各种约束条件下生产总成本最小。

1 模型描述

考虑产品的加工质量，对多产品多阶段的单机系统预防性维护与生产调度集成优化问题进行研究。以有限产能批量模型为基础，在考虑产品质量和产品换型成本的基础上，建立联合优化模型，利用SPC控制图对产品质量进行监控，当产品质量不在控制范围内时(产品质量在[LCL,UCL]间为合格产品)，立即对机器进行故障维修；当产品质量在控制范围内，需根据判异准则推测机器是否即将发生故障时，对机器进行预防性维修。

模型假设：①假设设备失效概率服从两参数的Weibull分布；②假设机器预防性维修与故障维修后都“恢复如新”，设备役龄清零；③每次预防性维护与故障维护的时间都为定值；④假设加工批量可分割，当产品加工时遇到故障进行维护，维护完后继续加工该批次；⑤假设出现不良品仅由设备原因导致，与人员、原材料、工艺方法和环境无关；⑥假设不同型号的产品质量控制界限相同；⑦假设产品质量服从正态分布；⑧假设产品质量在故障前后服从不同系数的正态分布。

1.1 变量的含义

模型参数：产品型号i∈P,P={A(i=1),B(i=2),C(i=3),…,N(i=n)}；

生产计划期T，生产周期tT，每个生产周期t大小均为τ；

ai：i产品的单位加工时间；

ui：i产品的单位加工成本；

hi：i产品的单位库存成本；

si：i产品的单位开机成本；

bi：i产品的单位缺货成本；

dit：i产品在周期t内的需求量；

ptcostij：在设备上从i产品换为j产品的成本；

Cp：预防性维护的成本；

Cr：故障维护的成本；

Tp：：预防性维护的时间；

Tr：故障维护的时间；

Ni：一个生产期内，设备生产i产品的最大产能；

Kmax：生产计划周期T内的最大产能约束；

M：设备进行预防性维护所需的累积运行时间阈值；

fi,t：周期t内故障维护情况下的设备运行时间累积；

Zt：在预防性维护和故障维护同时考虑的情况下设备运行时间累积；

Cst：生产换型成本；

xit：在生产周期t内，产品i的生产批量；

Sit：在生产周期t内，产品i是否进行开机生产；

Iit：在生产周期t内，产品i的库存量；

Bit：在生产周期t内，产品i的缺货数量；

PMit：在生产周期t内，生产产品i时发生预防性维护的次数；

NFit：在生产周期t内，生产产品i时发生故障维护的次数。

1.2 数学模型

模型主要考虑各个约束条件对生产成本的影响，以生产成本、库存成本、缺货成本、开机成本、换型成本与维护成本的生产总成本为优化目标，并利用SPC控制图对产品质量进行监控，依据不同的质量状态采取不同的维护措施。模型建立如下：

MinC=∑t∈T∑i∈P(uixit+hiIit+siSit+biBit) +

∑t∈TCst+∑t∈T∑i∈P(Cp·PMit+Cr·NFit)

(1)

Ii,t-1-Iit+xit=dit-Bit+Bit-1

(2)

xit≤NiSit

(3)

∑t∈T(PMit·Tp+∑i∈P(aixit+NFit·Tr) ) ≤Kmax

(4)

PMit·Tp+∑i∈P(aixit+NFit·Tr) ≤τ

(5)

fi,t=∑i∈P[(1-NFi-1,t)fi-1,t+aixit],f0,1=0=0

(6)

Zt=(1-PMi,t-1)Zt-1+fi,t,PMi,t=0=0

(7)

Zt≤M

(8)

Cst=∑i,j∈Pptcostij,(i,j∈P,i≠j)

(9)

xit≥0,Iit≥0,Bit≥0

(10)

Sit={0,1},PMit≥0,NFit≥0

(11)

式(1)是目标函数，旨在满足所有约束条件下最小化总成本：制造成本(生产批量成本、库存成本、开机成本和生产缺货成本)、换型成本、预防性维护成本与故障维护成本；式(2)是物料平衡约束条件：生产批量、库存量、需求量和缺货量之间保持平衡的方程；式(3)是i产品在t生产周期内的产能约束；式(4)是整个生产计划周期内的产能约束；式(5)是单个生产周期内的生产时间约束；式(6)是周期t内故障维护情况下的设备运行时间累积；式(7)是第t周期内的机器累积运行时间；式(8)是判断机器运行时间是否达到机器预防性维护的阈值；式(9)是计算整个计划周期内的换型成本；式(10)是变量生产批量、库存量和缺货量的约束条件；式(11)是开机变量、预防性维护次数和故障次数的约束条件。

1.3 维护策略

统计过程控制(Statistical Process Control，SPC)是质量管理的核心内容之一，它主要采用控制图来对过程是否处于统计控制状态进行判断和监控，具有动态、连续和实时等优点[12]。本文利用SPC控制图中的两个判异准则对设备是否需要预防性维护与故障维护进行判断，实时监控产品质量与设备运行情况。采用如下两个判异准则：

准则1：质量监测点落在控制界限之外；

准则2：连续6点递增或递减。

基于判异准则1的质量监控制定相应的设备故障维护策略；预防性维护采取判异准则2与基于设备累计运行时间的维护策略进行维护。设备维护后役龄清零，重新累计设备运行时间，当设备运行时间达到阈值时，进行预防性维护；当设备累积运行时间未达到阈值时，用SPC控制图监控产品质量，依据判异准则2判断是否需要预防性维护。

2 算法设计

2.1 染色体编码设计

为了解决生产批量与生产排序问题，设计如图1所示的染色体编码。

图1 染色体编码示意图

变量均采用实数编码，xit=(10 20 30 40 50 60 70 80 90 1 2 3 2 1 3 3 2 1)，染色体中的前9位数字表示三个产品(ABC)在三天(T=3)的生产批量，后9位数字表示每天各个产品的生产顺序。图1染色体表示第一天生产ABC产品的批量为10,20,30，生产顺序为ABC；第二天生产ABC产品的批量为40,50,60，生产顺序为BAC；第三天的生产批量为70,80,90，生产顺序为CBA。

中间变量中开机状态Sit，库存量Iit缺货量Bit，预防性维护次数PMit，故障维护次数NFit的染色体设计：Sit=( 1 0 0 | 1 0 1 | 0 1 0 )表示三天ABC产品的开机状态；Iit=( 10 20 30 | 40 50 60 | 70 80 90 )表示三天ABC产品的库存情况；Bit=( 10 20 10 | 20 30 10 | 30 10 20 )表示ABC产品的缺货情况；PMit=( 1 0 3 | 1 0 2 | 3 1 0 )表示三天ABC产品的预防性维护次数情况；NFit=( 4 0 2 | 1 2 2 | 2 1 0)表示三天ABC产品的故障维护次数情况。

2.2 适应度函数

式(1)是模型的适应度函数，表示以最小化总成本为优化目标。适应度函数受生产批量、生产排序、库存量、缺货量、开机状态、预防性维护与故障维护次数的影响。模型在综合考虑各个因素的影响下最小化生产总成本，得到最优的生产调度方案。

2.3 进化操作

2.3.1 变异操作

差分进化算法进行变异操作时，为了避免出现早熟现象，增加具有自适应变异的算子，根据算法搜索进展进行调整变异算子。

(12)

F=F0*2^(λ)

(13)

vi(gen+1)=xr1(gen)+F*(xr2(gen)-xr3(gen) )

(14)

式中，Fo为变异算子；Gm为最大进化代数；gen为当前进化代数，Vi(gen+1)为变异后的第gen+1代种群中第i个个体，xr1(gen)、xr2(gen)和xr3(gen)为gen代中不同的个体。在算法初期变异算子为Fo～2Fo，个体具有较大的多样性，避免早熟。随着算法的进展，变异算子逐渐降低，最后接近Fo，保留优良信息，避免最优解遭到破坏，增加搜索到全局最优解的概率。

2.3.2 交叉操作

交叉操作采用二项式交叉，通过随机选择，使得试验向量至少ui,j,g有一个分量由变异向量贡献[15]。交叉操作方程为：

(15)

其中，j=1,2,...,D;jrand为[1,D]内随机选择的整数，CR∈(0,1)为交叉率。

2.3.3 选择操作

选择操作采用精英保留策略，计算目标函数方法进行选择操作，淘汰掉不良个体。根据目标向量xig和试验向量ui,g的适应值f来选择最优个体，选择操作方程为：

(16)

式中，xi,g+1为下一代的目标向量。

2.4 算法流程

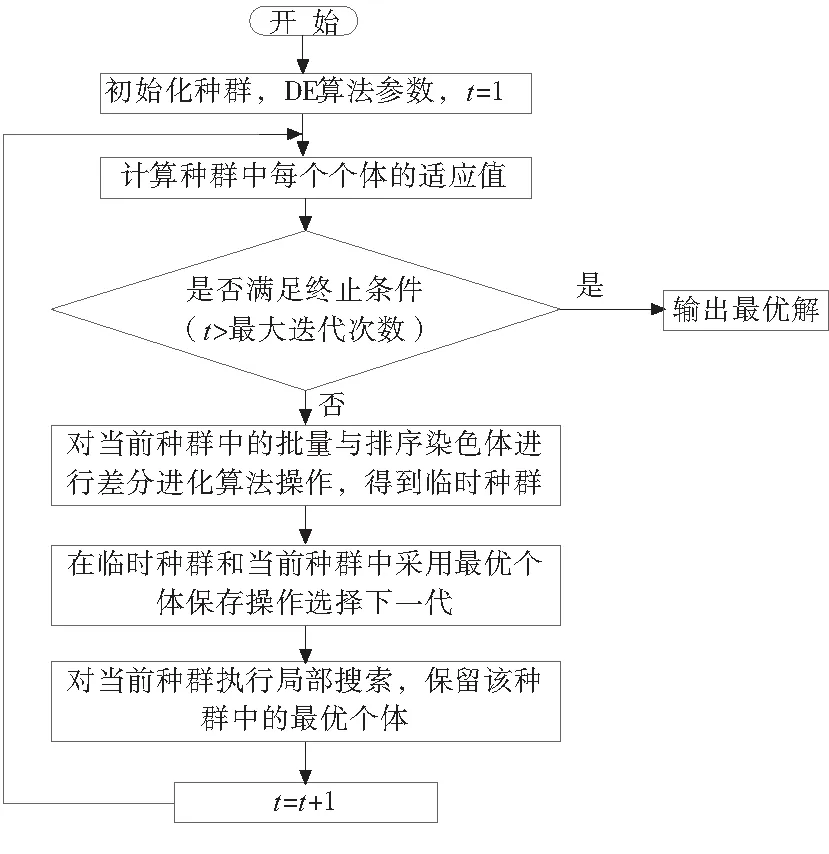
图2 算法流程图

图2为差分进化算法的流程图。计算初始种群的适应度函数值，通过变异、交叉和选择操作，保留种群中的精英个体。重复上述过程，迭代次，得到最优的生产调度方案。

在改革开放40年的浩荡浪潮中，改革和法治相伴而生、相向而行、相辅相成，共同推动和保障我国经济社会快速发展，同时也创造了我国40年改革开放的世界奇迹和法治发展的世界奇迹。

3 案例仿真

通过案例实验研究对模型进行验证，各参数如下：i=1,2,3表示ABC三个产品，t=1,2,3表示三个生产周期，初始库存为：Ii,t=1=[0,0,0]，Kmax=1000，M=20000，Cp=2400，Cr=5000，Tp=1，Tr=4.5。Np=50，Gm=500，Fo=1.3，CR=0.8，Ni=300，LCL=23，CL=25，UCL=27，其他数据如表1、表2和表3所示。

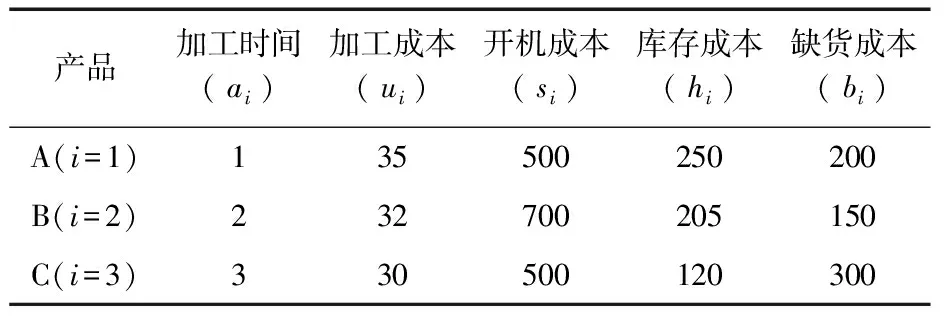
表1 各产品的参数

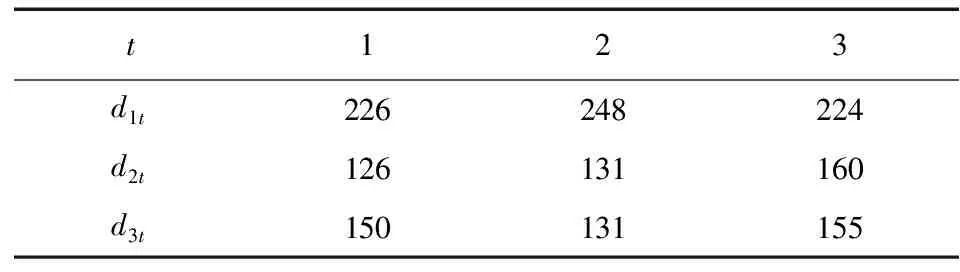
表2 各产品在不同时段的需求量

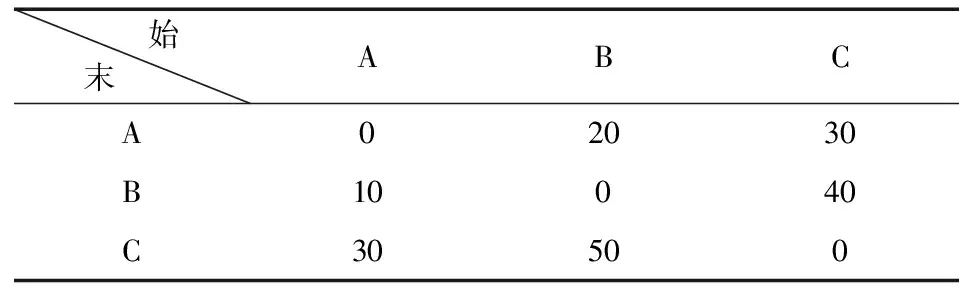
表3 各产品的换型成本

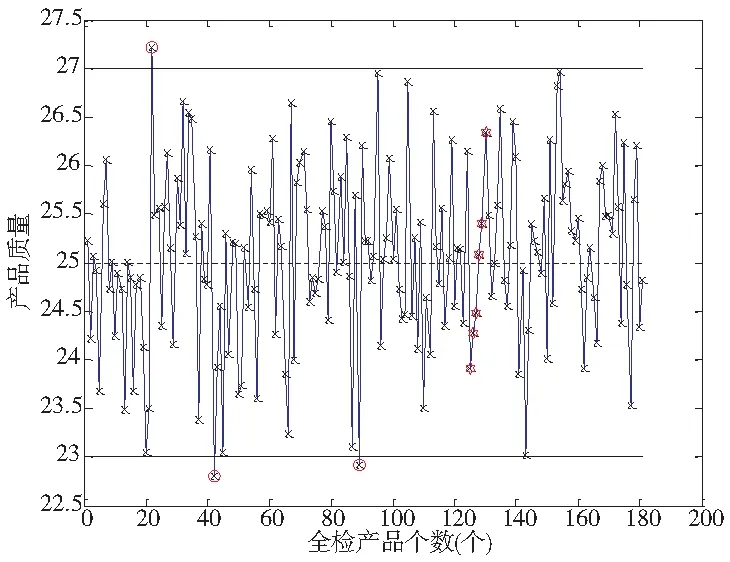
图3 第一天A产品SPC控制图

图4 第一天B产品SPC控制图

图5 第一天C产品SPC控制图

图6 目标函数值迭代过程

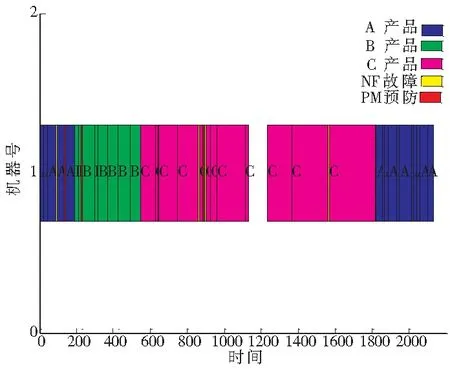
图7 生产调度甘特图

调度模型经过差分进化算法500次迭代计算后，得出模型的最优调度方案。图3～图5为最优调度方案中第一天产品生产的质量控制图；图6为利用差分进化算法计算目标函数值的迭代过程；图7为生产调度的甘特图，图中NF表示故障维护，PM表示预防性维护，甘特图表示在单机设备上三个产品三天的调度方案以及加工期间的预防性与故障维护情况。

调度方案求出了产品的生产批量和生产顺序，并给出了在该方案下的中间库存量、缺货量、开机状态、预防性维护与故障维护节点及次数，各变量值如下：Xit=(181 173 192 300 0 194 0 0 0 1 2 3 3 2 1 2 1 3)，库存量：Iit=(0 47 42 7 0 105 0 0 0)，开机状态：Sit=(1 1 1 1 0 1 0 0 0)，缺货量：Bit=(45 0 0 0 84 0 217 244 50)，预防性维护次数：PMit=(1 1 3 3 0 0 0 0 0)，故障次数：NFit=(3 6 8 10 0 2 0 0 0)，最优目标函数值：C=346536。

为了验证模型的有效性，设置一个对比试验：在相同实验参数条件下，采用定周期的预防性维护策略，不考虑产品加工质量对设备维护的影响。表4中数据都是在最优的生产调度方案下比较的。

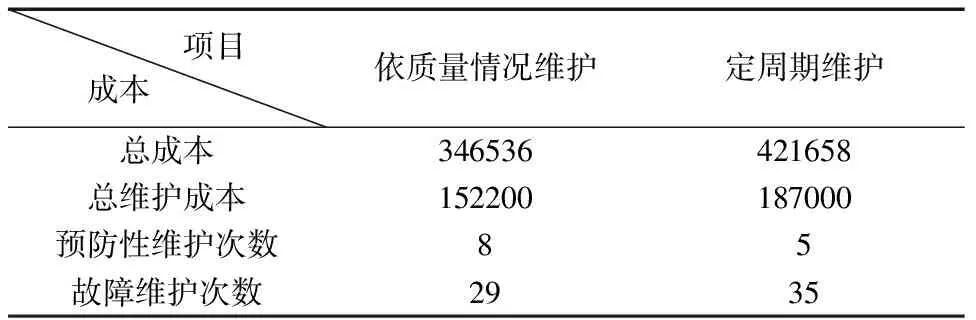
表4 定周期维护和依据质量情况维护的结果比较

通过对定周期的预防性维护和依据加工质量维护的结果对比可知，依据产品加工质量对设备进行维护可以降低生产的总成本，降低故障维护的次数。对比实验验证了本文所提出的模型的有效性。

4 结论

本文以单机系统为分析对象，基于CLSP模型，对生产调度与预防性维护进行集成优化研究。从两者耦合关系的角度建立了整体优化模型，克服了分开建模难以获得整体优化效果的弊端；为了避免算法求解中陷入局部最优解，设计了一种改进的差分进化算法对模型进行求解，获得了制造过程中的预防性维护与故障维护的时间节点、生产排序和批量分割方案，为生产决策者提供一个可靠的依据。

本文的研究方法为有效降低车间生产总成本和设备故障次数提供了一种可行的解决方案，对于同类制造车间生产总成本的有效控制具有良好的参考意义和价值。