面向流水车间的绿色生产多目标调度优化研究*

李 龙，王黎明，李方义

(山东大学 机械工程国家级实验教学示范中心，济南 250061)

0 引言

流水车间调度问题[1]通常可以描述为：一批待加工的工件集合，按照一定的顺序依次通过特定的加工系统进行加工，在满足一定约束条件的同时，通过调度工件加工顺序，合理分配系统资源，使得一些指标最优。流水车间调度作为典型的生产作业模式，在离散制造业中有着广泛的应用，因此对流水车间调度问题展开研究具有很重要的理论和工程应用价值。

对于流水车间生产调度问题，很多专家针对不同优化目标展开了研究。LIOU C D等[2-4]以车间生产时间为优化指标进行了探索，力求在最短时间内达到生产要求；张兴全等[5-6]对车间成本的调度优化进行了研究，以达到企业利益最大化；赵诗奎等[7-8]考虑环境问题对车间能耗调度优化展开了研究；文静[9]以AGV小车为主线进行能耗建模，针对车间总任务时间最短和总能耗最小两个目标采用帕累托优化方法进行了双目标优化。张超勇[10]以工件总成本最小和完成时间最短为指标，建立了加工成本和生产时间的数学模型，运用优化算法求解该调度问题。李聪波[11]引入特征元和加工元概念，建立以工艺路线总加工时间最短和总碳排放最低为优化目标的机械加工工艺路线多目标优化模型并进行调度优化。

从上述研究中可以看出，目前建立的模型多针对固定的单个或多个优化指标进行调度，具有较强的专一性与针对性。而车间实际生产过程中，经常面临企业生产效率亟待提升、经济效益需求增大以及环境问题日益严重等各方面的压力，车间需要随时根据企业外部需求选择相应的生产策略。所以如何面向流水车间建立一套可根据企业不同需求改变指标权重以适应实际生产的调度模型，获得符合实际生产状况的最优调度方案，增强生产的应变能力将会是本文的研究重点。

1 流水车间调度问题建模

根据流水车间生产特点，生产过程划分为：加工、调整、等待、运输4个阶段，各阶段之间的关联关系如图1所示。

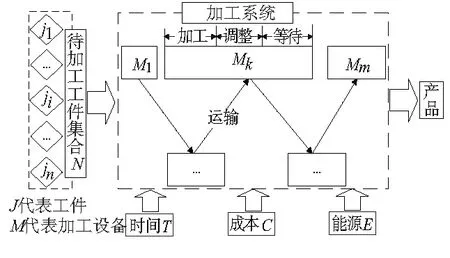
图1 流水车间生产运作过程

本文将加工、调整、等待阶段对应机床行为，运输阶段对应工件在不同机床之间的行为。流水车间每个工件的生产过程都要经过上述4个阶段，不同阶段产生相应的运作时间、生产成本及能耗。根据时间、成本和能耗在各阶段消耗的规律特点分别进行建立了相应的数学模型。

1.1 流水车间生产时间建模

工件总加工时间反映生产效率，良好的生产效率为车间按时完成生产任务提供保障。根据流水车间生产特点，假设工件的加工顺序为N{j1,j2,j3…ji…jn}，建立各时间的相关参数模型。

根据对生产过程各阶段的划分将流水车间的运作时间划分为加工时间、等待时间、调整时间、运输时间四部分(见图2)，建立数学模型如下：

T=PTtotal+WTtotal+ATtotal+TTtotal

(1)

图2 流水车间生产运作时间

(1)加工时间PTtotal为从工件到达后机床开始加工工件到完成加工需求所占用的时间。

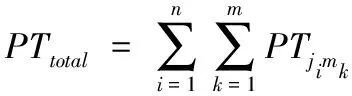
(2)

(2)等待时间WTtotal为机床加工工件时，由于工件未到达，机床等待产生的闲置时间，即上一个工序的结束时间到下一个工序的开始时间。

(3)

(3)调整时间ATtotal为上一工件结束加工后机床更换刀具、夹具为加工下一工件做准备占用的时间。

(4)

(4)运输时间TTtotal为将工件从上一台机床运送到下一台机床的时间。

(5)

1.2 流水车间成本建模

本文将成本按照各生产阶段进行详细划分，并考虑机床运行过程的耗电量也是成本的重要组成部分加入车间能耗成本。而机床调整时间较短，忽略调整带来的成本消耗。总能耗成本表示如下：

C=Pcost+Wcost+Tcost+Ecost

(6)

式中，C表示车间总成本；Pcost表示车间机床加工成本；Wcost表示车间机床等待成本；Tcost表示车间工件运输成本；Ecost表示车间能耗成本。

(7)

式中，UPC(mk)表示单位时间第k台机床加工成本。

(2)Wcost 1表示机床由于工件未到达，闲置空转过程产生的成本。

(8)

式中，UWC(mk)表示单位时间第k台机床等待成本。

(3)工件运输成本Tcost表示AGV小车将工件由上一台机床运送到下一台机床过程中产生的成本。

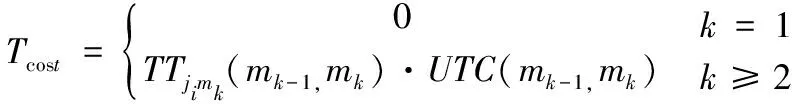
(9)

式中，UTC(mk-1，mk)表示单位时间将工件由第k-1台机床运输到第k台机床的运输成本。

(4)车间能耗成本Ecost是指车间内整个生产过程中总能耗产生的成本，由耗电量度量。根据我国工业电价的情况，取单位能耗成本0.725元/kW·h。

Ecost=(E·1000/3600)·(0.725)

(10)

式中，E表示车间加工总能耗。

1.3 流水车间能耗建模

本文将能耗作为车间调度的指标之一。根据车间生产运作特点，将能耗依次划分为：①机床能耗，包括生产运作过程中机床的加工能耗、等待能耗以及机床调整能耗；②运输能耗，包括车间运输各工件到相应的生产设备产生的能耗；③公共辅助能耗，包括车间看板、照明等辅助设施产生的各种公共能耗；通过对各部分能耗进行了详细的叙述分析与建模，最终得到流水车间加工产生的总能耗。

E=PE+WE+AE+TE+PCE

(11)

(1)机床能耗

①加工能耗PE为各机床在对工件进行加工的过程中产生的能量消耗。主要指工件进行生产加工时各机床的电量消耗。

(12)

式中，PEUnit(ji,mk)为单位时间第i个工件在第k台机床产生的加工能耗；m为加工工件的机床的总台数；n为工件的总个数。

②等待能耗WE为机床由于工件未到达而产生的闲置能耗，主要指机床空转和中间某些储能环节的能量消耗。

(13)

式中，WEUnit(mk)为单位时间第k台机床产生的等待能耗。

③调整能耗AE为机床加工上一工件结束后更换夹具、刀具等过程产生的能量消耗。

(14)

式中，AEUnit(ji,mk)为单位时间第i个工件在第k台机床产生的调整能耗。

(2)运输能耗TE为将工件由上一台机床运送到下一台机床进行加工的过程中产生的能量消耗。主要指AGV小车、叉车、传送带等运输工具执行运输功能时产生的能量消耗，多以用电量度量，本文取AGV小车耗电量作为运输能耗的主要来源。

(15)

式中，TEUnit(mk-1,mk)为单位时间将工件由第k-1台机床运送到第k台机床产生的运输能耗。

(3)公共辅助能耗PCE为整个加工过程中车间基础设施运行产生的能量消耗。主要包括看板、照明灯、排风扇等基础设施的能耗，且多以电量度量。

PCE=PCEUnit·Tf

(16)

Tf=F(jn,mm)-S(j1,m1)

(17)

式中，PCEUnit为单位时间基础设施消耗的公共能耗；Tf为工件加工结束时间。

2 流水车间生产运作模型转换与求解

2.1 流水车间生产运作模型转换

上述分别建立了流水车间生产过程中的时间、成本、能耗模型。在此基础上，本文综合三方面的需求将企业调度的多目标模型转换成单目标生产运作模型，如式(18)所示。在实际生产过程中，生产车间随时会面临工件完工时间缩短、工件生产成本减少、大力推进绿色性生产等突然改变的需求，传统的优化调度模型无法应对此类情况，本文提出的生产运作模型可随时根据需求的改变计算指标权重，建立符合实际需求的最优调度方案。

minZobject=α·fnorm(T)+β·fnorm(C)+γ·fnorm(E)

s.t.α+β+γ=1

T≤T0

E≤E0

C≤C0

(18)

式中，α为时间权重；β为成本权重；γ为能耗权重；T为车间生产总时间；C为车间生产总成本；E为车间总能耗；T0为车间加工时间约束；E0为车间加工能耗约束；C0为车间加工成本约束。fnorm(x)为归一化函数，为了消除时间、成本、能耗三个指标之间量纲[12]的影响。对于三种目标的权重问题，采用层次分析法[13](AHP)进行赋值，根据9标度法对指标权重进行打分，通过生成的判断矩阵，运用几何平均法计算各部分权重，经过一致性检验后，得到合适的权重系数。

车间生产运作过程中面临不同的生产需求，对应产生不同的车间调度模式。本文综合考虑流水车间的多种生产情况，将车间模式划分为综合模式、高效模式、节能模式、经济模式4种典型的生产模式，并对各模式进行AHP决策，得到相应模式下的权重，为车间生产提供指导，具体如表1所示。

表1 典型生产模式

其中，综合模式将车间的时间、成本、能耗三方面指标进行综合评分，各指标权重差别较小，企业注重三方面均衡发展；高效模式是指企业优先偏重生产效率的需求，以获取工件最短生产时间作为首要任务；节能模式是指能耗对企业生产过程约束较大，企业更注重生产过程对环境产生的影响，以环境问题为主要考量指标；经济模式是指企业以工件最小生产成本为需求，更注重企业利益，将经济性问题作为首要目标。

2.2 流水车间的单目标生产运作模型求解

遗传算法[14](Genetic Algorithm)是以遗传理论和自然选择为基础，将生物进化过程中适者生存规则与群体内部染色体信息随机交换机制相结合的高效寻优搜索算法，具有多目标优化、全局优化、较强鲁棒性等优点。本文面向流水车间选取遗传算法对生产运作模型进行寻优迭代，得到最优调度方案。迭代步骤如图3所示。

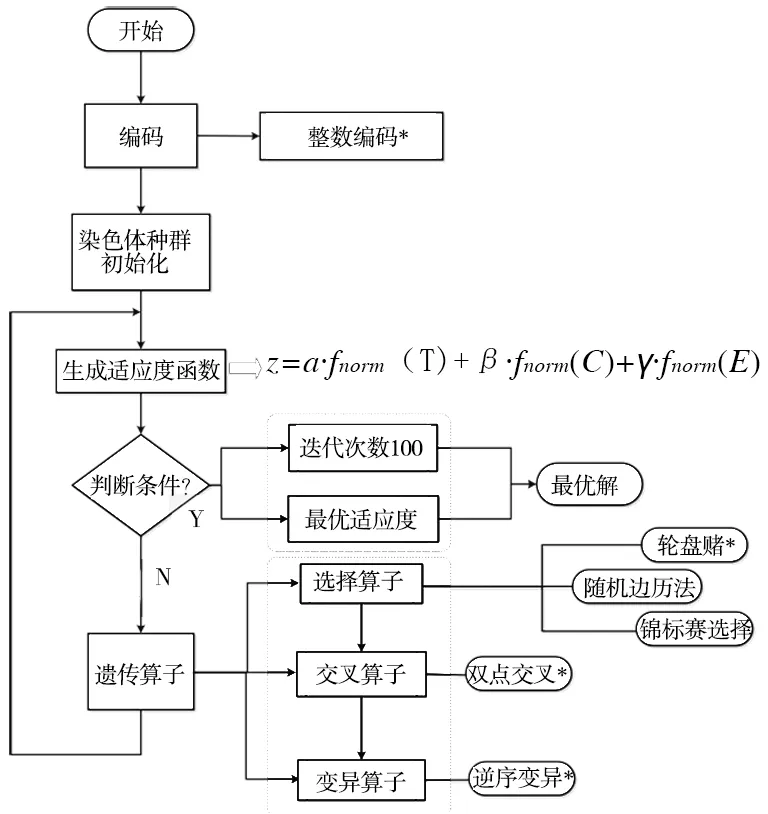
图3 迭代步骤流程图

3 案例分析

本文以某机械加工作业车间为研究对象，对模型有效性和准确性进行验证。齿轮零件按照一定顺序：钻孔→车外圆→滚齿→磨外圆，依次经过流水线上各机床进行加工成型。各零件在每台机床对应各阶段的时间、能耗通过CW240功率测试仪实际测量获得，功率仪每隔100ms采集一次机床功率数据，并通过AP240E数据处理得到具体耗值。机床单位时间加工成本、等待成本、工件运输成本等通过调研国内目前加工市场以及咨询操作工人获得，具体数据矩阵如表2所示。

表2 生产运行数据

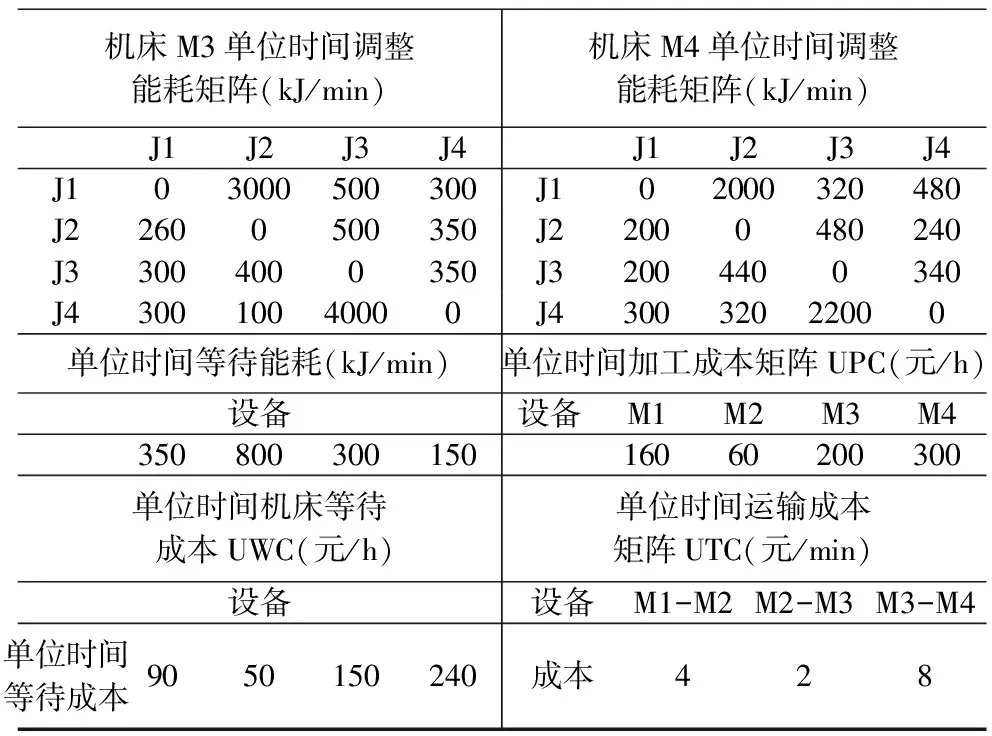
续表

单位时间公共能耗(kJ/min)UnitUCE=90。

企业可根据车间工件生产情况对时间、成本、能耗的范围进行界定，通过GA迭代三个指标的范围分别取：时间[46，59]，成本C∈[428，519]，能耗E∈[57730,80560]。应用AHP方法对各指标权重α、β、γ进行决策时，不同的指标权重对应不同的调度优化方案。本生产车间分别对上文提到的4个典型的生产模式：综合模式(均衡各指标)、高效模式(偏注重时间)、节能模式(偏注重能耗)、经济模式(偏注重成本)进行寻优迭代，求解此加工车间各模式下的调度优化顺序。

本文以归一加权得到的模型Zobject=α·fnorm(T)+β·fnorm(C)+γ·fnorm(E)作为目标函数，利用遗传算法，设定初始种群规模20个，迭代次数设为100，交叉概率设为0.7，变异概率设为0.01，在不同生产模式下运行MATLAB程序对生产调度问题进行求解。4个模式经过分析后得到的调度优化结果以及各模式指标的具体耗值如表3所示。

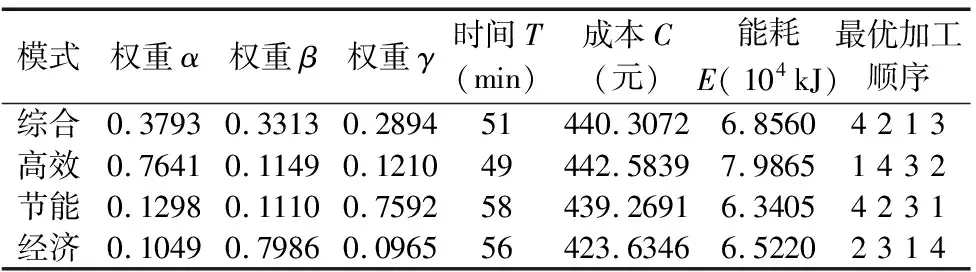
表3 运行结果分析对比

由表3可以看出，对于综合模式，三方面均衡发展，其各项指标的值在其他模式对应指标值之间；对于高效模式，企业更能看重生产时间，以最快时间完成任务为首要目标，时间较其他方案最短为49min；对于节能模式，企业关注节能降耗，能耗较其他方案最小为63405kJ；对于经济模式，企业注重追求利益最大化，成本较其他方案最少为423.6364元。各生产模式可以在不同生产需求的情况下有不同的应用。

生成的各模式下生产任务甘特图(图4～图7)清晰的表达出各工件的各时间关系，结合生产工件的各指标数据进一步对比各模式之间的特点。

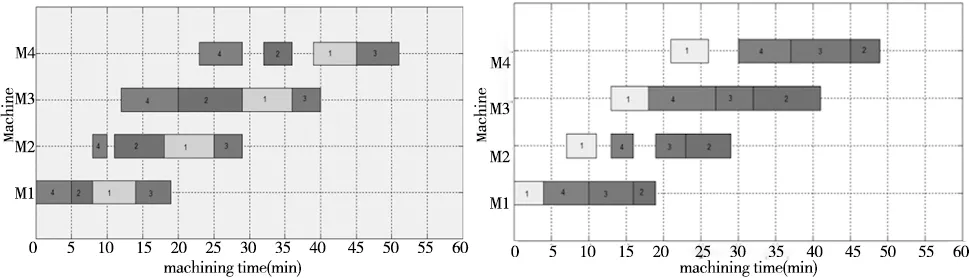
图4综合模式生产任务甘特图 图5高效模式生产任务甘特图

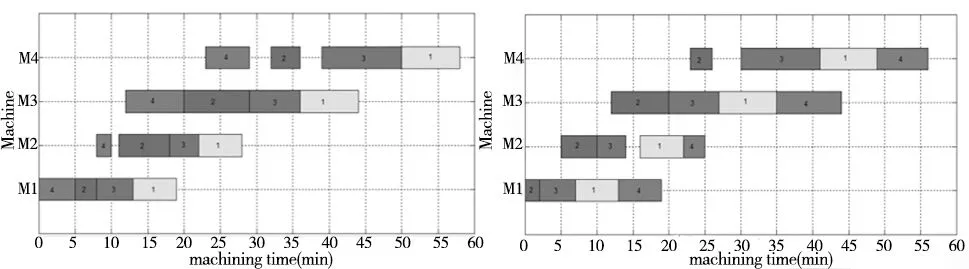
图6节能模式生产任务甘特图 图7经济模式生产任务甘特图

综合模式适用于企业在生产过程中没有特殊要求，平衡、稳定的生产情况。此种模式能全面的考虑生产的各项指标问题，促使效率、经济、环境稳步发展，其对应的各时间、成本、能耗值如表3所示。

高效模式适用于生产任务紧迫，需要提高生产效率，尽快完成加工的情况。等待时间与调整时间作为时间的主要变量因素。从各机床上调整时间矩阵可以看出机床M3上工件j2→j3，j4→j1的调整时间远大于其他工件，所以机床M3加工工件时避免工件j2→j3调整或工件j4→j1的调整。对比高效模式与综合模式，两个模式都避免了机床M3上工件j2→j3，j4→j1的加工顺序，调整时间相差不大，所以等待时间成为获取高效模式的重要因素，通过对比综合模式与高效模式的生产任务甘特图可以看出高效模式在机床M2、M4上总等待时间明显少于综合模式，且由优化结果可知等待时间的减少导致了高效模式的时间比综合模式减少近4.08%。

节能模式适用于企业生产过程因能耗产生过多，造成环境严重污染，必须采用清洁生产的情况。调整能耗、等待能耗与公共能耗作为能耗的主要变量因素，从调整能耗矩阵得出机床M3上j1→j2，j4→j3，机床M1上j3→j4的调整能耗远大于其他工件，所以机床M1上应避免j3→j4的调整，机床M3上应避免j1→j2，j4→j3的调整。对比节能模式与高效模式，两个模式都避免了此类加工顺序，从单位时间等待能耗矩阵得出机床M4的单位时间等待能耗最小，而机床M2的单位时间等待能耗最大，约为机床M2的5.3倍，所以在机床M2进行工作时，机床等待时间最短，相应的机床M4上等待的时间变长。经计算得知高效模式的调整能耗约为节能模式调整能耗的4.27倍，公共能耗相差不大，综合各能耗因子，节能模式的能耗比高效模式能耗减少了25.96%，时间相对增加较少，能耗变化显著。

经济模式适用于企业以获取最大利润为前提进行生产的情况。通过分析，加工成本与运输成本为不可变量，加工成本和等待成本在总成本中占84.34%以上，运输成本次之，能耗成本最少。因此通过控制等待成本是减少加工总成本的有效方法。等待成本作为成本的主要影响变量，从单位时间等待成本矩阵可得机床M4的单位时间等待成本最大，所以机床M4的等待时间应该较少。对比经济模式与节能模式，经过计算求得能耗模式的能耗成本为12.7691、等待成本为200，经济模式的能耗成本为13.1346、等待成本为184，所以综合各成本因子，经济模式的成本比节能模式的成本降低3.69%，节能模式的能耗比经济模式降低2.86%。

4 总结

(1) 本文面向流水车间，综合考虑了生产约束与生产压力，根据零件生产过程不同阶段的划分，建立生产加工过程的时间、成本、能耗指标模型，基于归一加权方法，将多目标函数转换为单目标生产运作模型，通过层次分析法决策得到各指标权重，随时通过调整权重以符合实际生产情况，并运用GA优化算法获得最优方案。

(2) 根据流水车间生产需求，提出综合、高效、节能、经济四种典型的生产模式，通过专家根据九标度法打分生成的判断矩阵计算得到各生产模式的指标权重。企业可根据车间生产需求，依据敏感性分析选择相应模式的权重进行调度优化，获取符合实际情况的调度方案。

(3)本文的研究对象是针对各零件加工工序相同，各工序只能在一台机床上加工的流水车间，可进一步向各工件加工过程存在并行设备的混合流水车间或其他生产车间进行拓展。